Идентифицировать закон распределения генеральной совокупности
1 Кузнецов А.А., Судаков Е.Н. Расчеты основных процессов и аппаратов переработки углеводородных газов: Справочное пособие. — М.:Химия, 1983. — 224 с., ил.
УНИВЕРСИТЕТ КАФЕДРА ИЗМЕРИТЕЛЬНЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ О Т Ч Е Т по расчетному заданию по курсу «Теория вероятностей»
Работу выполнил студент группы 2085/21: Гаранин В.А. “ “ декабря 2012г. Работу принял: __________________ /фамилия, инициалы преподавателя/ ______________________________ /Подпись преподавателя, дата/
Санкт–Петербург Задание на расчетную работу по курсу «Теория вероятности и математическая статистика» В результате измерений получена выборка x 1, x 2,..., xn, n =201 из генеральной совокупности с неизвестным законом распределения. 1. Построить на основе выборки: 1.1. выборочную функцию распределения F (x); 1.2. гистограмму; 2. Вычисление точечных оценок по всей выборке: 2.1. первого начального момента, 2.2. второго, третьего и четвертого центральных моментов по выборочной функции распределения, Для оценки первого начального момента использовать среднее арифметическое, выборочную медиану, середину размаха; 2.3. коэффициентов асимметрии и эксцесса, 2.4. границ интерквантильного промежутка J p вероятностной меры P = 0,95; 2.5. характеристики по пп. 2.1-2.3 по отдельной части исходной выборки содержащей 20 значений (указанная часть выборки извлекается из произвольного места исходной выборки); 3.Интервальные оценки с доверительной вероятностью Q = 0,8: 3.1. первого начального и второго центрального моментов (вычисления выполнить по полной выборке и по ее части, выбранной в пункте 2.4), 3.2. интерквантильного промежутка J для P = 0,95 (по всей выборке с помощью непараметрических толерантных пределов); 3.3. интерквантильного промежутка J для P=0,95 (для части выборки с помощью параметрических толерантных пределов); Идентифицировать закон распределения генеральной совокупности Идентифицировать методом проб, определяя параметры закона (если моменты параметрами не являются), и проверяя для каждой пробы гипотезу о соответствии предполагаемого закона распределения экспериментальным данным с помощью одного из двух критериев: Колмогорова-Смирнова, “омега-квадрат”. Для начальной ориентировки в выборе закона использовать вид гистограммы, соотношения между моментами и полученные значения асимметрии и эксцесса.
1. Построить на основе выборки: 1.1. выборочную функцию распределения F (x); Расчеты были произведены в инженерной системе MatLab (код приведен в Приложении 1)
Рис.1 Выборочная функция распределения 1.2 гистограмму распределения;
Рис.2 Гистограмма распределения 2. Вычисление точечных оценок по всей выборке: 2.1. первого начального момента, Первый начальный момент (математическое ожидание) вычисляется через среднее арифметическое по формуле:
и равняется -2,0620. Через выборочную медиану: Через середину размаха: 2.2. второго, третьего и четвертого центральных моментов по выборочной функции распределения, Второй, третий и четвертый центральные моменты считаются по формулам:
2.3. коэффициентов асимметрии и эксцесса, которые рассчитываются по формулам:
2.4. границ интерквантильного промежутка J p вероятностной меры P = 0,95; Границы рассчитываются следующим образом:
выборочную функцию распределения и провести линии на уровне 0,025 и 0,975 можно увидеть, что для нахождения границ интерквантильного промежутка мы имеем право откинуть по одному значению с краев выборки
Рис.3 Определение верхней границы интерквантильного промежутка
Рис.4 Определение нижней границы интерквантильного промежутка Значит интерквантильный промежуток Jp=[ -3,2315; -1,1173] 2.5. характеристики по пп. 2.1-2.3 по отдельной части исходной выборки содержащей 20 значений (указанная часть выборки извлекается из начала исходной выборки); Все оценки для этого пункта вычисляются по тем же формулам, что и в пунктах 2.1-2.3, с тем лишь изменением, что значений будет не 201, а 20, следовательно:
3. Вычислить интервальные оценки с доверительной вероятностью Q = 0,8: 3.1. первого начального и второго центрального моментов (вычисления выполнить по полной выборке и по ее части, выбранной в пункте 2.4), Интервальная оценка математического ожидания вычисляется по формуле:
Интервальная оценка математического ожидания равна: [-2.0654; -2.0587] Вычисления по части выборки производятся по аналогичным формулам и для 20 значений интервальная оценка математического ожидания равна: [-1,9025; -1.8358]
Интервальная оценка для дисперсии вычисляется по формулам:
Интервальная оценка для дисперсии равна: [0,2410; 0,3115]. Вычисления по части выборки производятся по аналогичным формулам и для 20 значений интервальная оценка дисперсии равна: [0,1760; 0,4110]. 3.2. интерквантильного промежутка J для P = 0,95 (по всей выборке с помощью непараметрических толерантных пределов, симметричных относительно среднего арифметического); Согласно таблице "Минимально необходимый объем выборки для нахождения непараметрических толерантных пределов, накрывающих с доверительной вероятностью Q интерквантильный промежуток вероятностной меры 0,8, K=3 следовательно непараметрическими толерантными пределами мы имеем право взять 2 и n-2 значения вариационного ряда. Таким образом, непараметрические толерантные пределы будут: [-3.3845,-0.9100] 3.3. Интерквантильного промежутка J для P=0,95 (для части выборки с помощью параметрических толерантных пределов); Параметрические толерантные пределы находятся по формулам:
В нашем случае параметрические толерантные пределы будут: [-3.0558,-0.6824]
|



 , где n – количество элементов в выборке, в нашем случае 201,
, где n – количество элементов в выборке, в нашем случае 201,

 , где
, где  - среднее арифметическое
- среднее арифметическое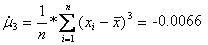

 = - 0,0471, либо с помощью функции MatLab – Skewness(значения получились одинаковыми)
= - 0,0471, либо с помощью функции MatLab – Skewness(значения получились одинаковыми)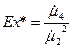 = 3,0356, либо с помощью функции MatLab – Kurtosis(значения получились одинаковыми)
= 3,0356, либо с помощью функции MatLab – Kurtosis(значения получились одинаковыми) - P -
- P -  ;
;  ;
;  следуя из этого, если посмотреть на
следуя из этого, если посмотреть на

 =-1,8692, где, для этого пункта, n = 20, xi – значения выборки из 20 значений от исходной выборки.
=-1,8692, где, для этого пункта, n = 20, xi – значения выборки из 20 значений от исходной выборки.
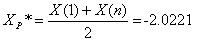



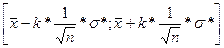 , где k – это
, где k – это  *100%-ая квантиль Стьюдента с (n-1) степенями свободы, и вычисляется в MatLab:
*100%-ая квантиль Стьюдента с (n-1) степенями свободы, и вычисляется в MatLab:  = 1,2858, а
= 1,2858, а  - эффективная оценка среднеквадратичного отклонения (с.к.о), и вычисляется по формуле:
- эффективная оценка среднеквадратичного отклонения (с.к.о), и вычисляется по формуле:  = 0.5219.
= 0.5219. , где
, где  - эффективная оценка дисперсии и равна:
- эффективная оценка дисперсии и равна: = 0,2723, а k1 и k2 соответственно
= 0,2723, а k1 и k2 соответственно  ая и
ая и  ая квантили распределения хи-квадрат и вычисляются в MatLab по формулам:
ая квантили распределения хи-квадрат и вычисляются в MatLab по формулам: = 226,0210
= 226,0210 = 174,8353
= 174,8353 , где k = 2.3637 - параметрический толерантный множитель, взятый из таблицы значений параметрических толерантных множителей для оценки границ 95%-го интерквантильного промежутка нормального распределения с доверительной вероятностью Q по выборке из n=20 значений.
, где k = 2.3637 - параметрический толерантный множитель, взятый из таблицы значений параметрических толерантных множителей для оценки границ 95%-го интерквантильного промежутка нормального распределения с доверительной вероятностью Q по выборке из n=20 значений.


