Pierre de Fermat
P. Fermat (1601-1665) must be awarded the honour of being the founding father of number theory as a systematic science. His life was quiet and uneventful and entirely centred around the town of Toulouse, where he first studied jurisprudence, practised law, and later became prominent as councillor of the local parliament. His leisure time was devoted to scholary pursuits and to a voluminous correspondence with contemporary mathematicians, many of whom, like himself, were gentlemen-scholars, the ferment of intellectual life in the seventeenth and eighteenth centuries. Fermat possessed a broad knowledge of the classics, enjoyed literary studies, and wrote verse, but maths was his real love! He published practically nothing personally, so that his works have been gleaned from notes that were preserved after his death by his family, and from letters and treatises that he had sent to his correspondents. In spite of his modesty, Fermat gained an outstanding reputation for his math achievements. He made considerable contributions to the foundation of the theory of probability in his correspondence with Pascal and introduced coordinates independently of Descartes. The French often interject the name of Fermat as a cofounder of the calculus, and there is considerable justification for this point of view. In spite of all these achievements, Fermat's real passion in maths was undoubtebly number theory. He returned to such problems in almost all his letters; he delighted to propose new and difficult problems, and to give solutions in large figures that require elaborate computations; and most important of all, he announced new principles and methods that have inspired all work in number theory after him. Fermat's factorization method (which is the point interesting us particularly) is based upon the following facts. If a number
On the other hand, if
Since we deal with the question of factoring Since Fermat's method is particularly helpful when the number Of particular interest is Fermat's last theorem. Greek maths, as is known, was geometric in character. However, during the later Alexandrian period, the algebraic methods came more into the foreground. During this period, Diophantus (A.D. 250), the most renowned proponent of Greek algebra, lived in Alexandria. Nothing is known about his life. All his books deal with the properties of rational and integral numbers, topics on algebraic equations and more particularly with the solution of certain problems in which it is required to find rational numbers satisfying prescribed conditions. More than 130 problems of this latter type are discussed, and Diophantus shows great ingenuity in devising elegant methods for their solution. The path from Diophantus to Fermat although long in time, is quite direct. Fermat represents a focal point in the history of number theory; in his work the radiating branches of earlier periods were united and their content recreated in a richer and more systematic form. Fermat possessed a well-known copy of Diophantus, which he also used as a notebook. In the margins he jotted down several of his most important remarks as they occurred to him in connection with the related problems in Diophantus. We now come to the most famous of Fermat's remarks in his copy of Diophantus. In problem 8 in Book II Diophantus propounds: "To decompose a given square number into the sum of two squares. " To use a general notation, let This problem to us is quite straightforward, but it was not always so. In the oldest preserved Diophantus' manuscript, copied in the thirteenth century we find at this point the following heartfelt remark by the writer: "Thy soul, Diophantus, to Satanas, for the difficulty of thy problems and this one in particular." Fermat's comments in connection with this problem are as one should expect considerably more constructive and of much greater consequence: "However, it is impossible to write a cube as the sum of two cubes, a fourth power as the sum of two fourth powers and in general any power beyond the second as the sum of two similar powers. For this I have discovered a truly wonderful proof, but the margin is too small to contain it." This is the famous Fermat's theorem, sometimes called Fermat's last theorem, on which the most prominent mathematicians have tried their skill ever since its announcement three hundred years ago. In algebraic language, it requires that it shall be shown that the Diophantine equation Fermat's problem has remained remarkably active throughout its history, and results and research on it still appear frequently in the math journals. It must be admitted frankly that if the specific result implied in the theorem were obtained, it would, probably, have little systematic significance for the general progress of maths. However, the theorem has been extremely important as a goal and a constant source of new efforts. Some of the new methods it has inspired are basic nowadays not only for number theory but also for many other branches of maths.
|

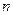 can be written as the difference between two square numbers, one has the obvious factorization
can be written as the difference between two square numbers, one has the obvious factorization (1)
(1) ,
,  is composite, one can obtain a representation (1) of
is composite, one can obtain a representation (1) of  ,
,  sothat
sothat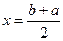 ,
, 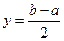 (2)
(2) and
and  are odd and the values of
are odd and the values of 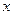 and
and  are integral. Corresponding to eachfactorization of
are integral. Corresponding to eachfactorization of 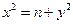 .
. , one has
, one has  . The procedure consists in substituting successively for
. The procedure consists in substituting successively for  and examining whether the corresponding,
and examining whether the corresponding,  is a square
is a square  .
. is relatively small, because a suitable у will then quickly appear. By means of certain other improvements that can be introduced in the procedure, it becomes one of the most effective factorization methods available.
is relatively small, because a suitable у will then quickly appear. By means of certain other improvements that can be introduced in the procedure, it becomes one of the most effective factorization methods available. be the given square for which one wants to find
be the given square for which one wants to find  . As usual, Diophantus asks for rational solutions.
. As usual, Diophantus asks for rational solutions. has no solution in integers,
has no solution in integers,  , all different from zero, when
, all different from zero, when 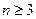 . The question whether Fermat possessed a demonstration of his last problem will in all likelihood forever remain an enigma. Fermat, undoubtedly, had one of the most powerful minds ever applied to investigate the laws of numbers, and from his indications there is every reason to believe that he was able to prove the various other assertions that he included in the Diophantus notes. The remark that the margin was too small may, perhaps, sound a bit like an excuse, but it was an observation he had to make also in other instances.
. The question whether Fermat possessed a demonstration of his last problem will in all likelihood forever remain an enigma. Fermat, undoubtedly, had one of the most powerful minds ever applied to investigate the laws of numbers, and from his indications there is every reason to believe that he was able to prove the various other assertions that he included in the Diophantus notes. The remark that the margin was too small may, perhaps, sound a bit like an excuse, but it was an observation he had to make also in other instances.


