ЦДТ "УНИВЕРМАГ", 1 ЭТАЖ
Кафедра: менеджмента Дисциплина: Анализ хозяйственной деятельности
Лабораторная работа №2. Группировка и КРА.
Выполнила: студентка группы 5МО-31 Широких И.П. Проверила: преподаватель Неробова В.А.
Череповец 2012 Цель работы: используя средства MS Excel проводить группировку и КРА. Задание: Построить простую аналитическую группировку. Результативным показателем является годовое жалование (дол.). Таблица 1
Алгоритм решения: 1. Рассчитаем шаг группировки по формуле:
Образование = (6-0)/4=1,5≈2
2. Строим рабочую таблицу “Группировка по образованию”: Таблица 2
3. Остаточная дисперсия:
где
j =1,2,3,…, m.
4. Средняя величина внутригрупповой дисперсии:
5. Межгрупповая дисперсия:
6. Общая дисперсия:
7.Рассчитаем эмпирическое корреляционное отношение, которое измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор.
Построим точечные диаграммы рассеяния: 1.1. Зависимость зарплаты от во з раста 1.2. Зависимость зарплаты от стажа 1.3. Зависимость зарплаты от пола 1.4. Зависимость зарплаты от уровня образования. Определим тесноту связи с помощью функции КОРЕЛЛ:
1.1. В первом случае выделяем массивы «возраст» и «зарплата»: Ответ 0,993579 – это означает, что между возрастом и зарплатой существует очень сильная линейная прямая корреляционная зависимость:
Рис.1. 1.2. Зависимость зарплаты и опыта. Теснота связи: 0,972792. Таким образом, между стажем и зарплатой также существует очень сильная линейная прямая корреляционная зависимость:
Рис.2. 1.3 Зависимость зарплаты от пола – очень слабая линейная прямая корреляционная зависимость (0,275515).
Рис.3.
1.4 Зависимость зарплаты от уровня образования. Теснота связи = - 0,7648946 Это высокая обратная линейная корреляционная зависимость.
Рис.4
2) Определим параметры уравнения многофакторной регрессии, используя функции "Линейн" и "лгрфприбл" Выделяем диапазон ячеек 5х5. Вызываем функцию «Линейн»: В первой строке массив данных результативного показателя (зарплата), во второй – факторного показателя. После заполнения всех строк, нажимаем ctrl+shift+Enter. Получаем:
Уравнение множественной линейной регрессии имеет следующий вид: у=1064,032х1+ 822,1468х2+1295,648х3+575,342686х4-2829,036 Коэффициент детерминированности. Коэффициент r2=0,998215545. (т.е. между оценочным и фактическим значениями у нет особых различий) Вызываем функцию FРАСПОБР. Вероятность равна 0,05; Степень свободы 1 равна 4 (v1 = n – df – 1= 20-15-1=4); Степень свободы 2 равна 15 (v2 = df) Нажмем ОК. F- критическое равно 3,05556828. F-наблюдаемое равно 2097, 73197
2097,73197>3,05556828, F- наблюдаемое>F-критическое, т.е. r2 статистически значим. Вычислим T-статистику для линейной функции, поделив mi на sei: Tнабл1= 575,342686/256,066959=2,246845. Tнабл2= 1295, 648/702,1832=1,845171 Tнабл3=9,46542 Tнабл4=20,38225 Tнабл5= -1,36082 Воспользуемся функцией СТЬЮДРАСПОБР. Сделаем выводы по критерию Стьюдента, сравнив Т-наблюдаемое значение с критическим: Вызовем функцию “СТЬЮДРАСПОБР”. Вероятность: 0, 05; Степени свободы: 15. Нажмем ОК. Ткр= 2, 13144954 tнабл1>tкр,, tнабл3>tкр, tнабл4>tкр, т.е. можно сделать вывод о том, что статистическая значимость соответствующего коэффициента регрессии подтверждается. tнабл2>tкр, tнабл5>tкр, т.е. можно сделать вывод о незначимости коэффициента регрессии. Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
2.2. Уравнение множественной регрессии (кривой для " ЛГРФПРИБЛ ") имеет следующий вид: y = (b*(m1^x1)*(m2^x2)*_) (в случае нескольких значений x), где зависимые значения y являются функцией независимых значений x. Значения m являются основанием, возводимым в степень x, а значения b постоянны. Функция ЛГРФПРИБЛ возвращает массив {mn; mn-1;...; m1; b}.
На Листе Microsoft Excel выделяем диапазон ячеек 5 Известные значения y: выделяем диапазон ячеек F10:F29, т.е. столбец зарплата; Известные значения х: выделяем диапазон ячеек B10:Е29, т.е. всю остальную часть таблицы со столбцами возраст, опыт, пол, образование; Конст и Статистика равны 1, условие “ИСТИНА”.
Далее нажимаем cntrl+shift+Enter. Получаем следующую таблицу: Таблица 4
Значения таблицы соответствуют значениям на рисунке 1. Следовательно, уравнение множественной регрессии (кривой для " ЛГРФПРИБЛ ") будет иметь следующий вид: y=(16969,36*(1,021409^x1)*(1,015544^ x 2)*(0,97817151^x3)*(1,0048131^x4)
Коэффициент детерминированности: r2= 0,963838 (т.е. между оценочным и фактическим значениями у нет особых различий)
Вызываем функцию FРАСПОБР. Вероятность равна 0,05; Степень свободы 1 равна 4 (v1 = n – df – 1= 20-15-1=4); Степень свободы 2 равна 15 (v2 = df) Нажмем ОК. F- критическое равно 3,05556828. F-наблюдаемое равно 99,95084
99,95084>3,05556828, F- наблюдаемое>F-критическое, т.е. r2 статистически значим.
Вычислим T-статистику для функции ЛГРФПРИБЛ, поделив ln mi на sei: Tнабл1= 0,004802/0,023133=0,20756802. Tнабл2= -0,347923 Tнабл3= 1,965772 Tнабл4= 4,491816 Tнабл5= 51,85719 Воспользуемся функцией СТЬЮДРАСПОБР. Сделаем выводы по критерию Стьюдента, сравнив Т-наблюдаемое значение с критическим: Вызовем функцию “СТЬЮДРАСПОБР”. Вероятность: 0, 05; Степени свободы: 15. Нажмем ОК. Ткр= 2, 13144954 tнабл1<tкр, tнабл2<tкр, tнабл3<tкр, т.е. коэффициент регрессии незначим. tнабл4<tкр, tнабл5<tкр, т.е. можно сделать вывод о том, что статистическая значимость соответствующего коэффициента регрессии подтверждается, значит данные не противоречат гипотезе о равенстве нулю истинного значения коэффициента Контрольное задание: Проведите корреляционно-регрессионный анализ, используя функции «линейная» и «корреляция». Сделайте оценку по критериям Стьюдента и Фишера. Составьте прогноз ожидаемого объема продаж в будущем периоде, используя функцию «Предсказание».
Воспользуемся функцией ЛИНЕЙН: Рассчитаем коэффициент Стьюдента 3 способами: 1) t=mi / sei: 0,616982/0,1182=5,219798 2) извлечь из корень F- статистики: 3)) t= где,
Найдем коэффициент корреляции. Для этого вызовем функцию “КОРРЕЛ”. Значение коэффициента корреляции составляет 0,855288. Таким образом, подставив это число в формулу получаем: t=5,219798 Вычислим T-статистику для линейной функции, поделив mi на sei: Tнабл= 0,616982/0,1182=5,2198.
Воспользуемся функцией СТЬЮДРАСПОБР. Сделаем выводы по критерию Стьюдента, сравнив Т-наблюдаемое значение с критическим: Ткр= 2, 228139 (вероятность 0,05, степень свободы 10) tнабл>tкр, т.е. 5,2198>2,228139, т.е. можно сделать вывод о том, что статистическая значимость соответствующего коэффициента регрессии подтверждается. (Коэффициент корреляции равен 0,731517, между двумя факторами (расходы на рекламу и продажи) существует высокая прямая линейная зависимость).
Рассчитаем критерий Фишера по формуле: F =
Fнабл =
Вызываем функцию FРАСПОБР. Находим F-критическое. Fкр= 4,9646027. (вероятность - 0,05, степень свободы1 – 1, ступень свободы2 – 10)
27,246296>4,9646027, F- наблюдаемое>F-критическое, т.е. r2 статистически значим. Составим прогноз ожидаемого объема продаж в будущем периоде, используя функцию «Предсказание». Вызываем функцию “ПРЕДСКАЗ”: Х- данное прогнозное значение по расходам на рекламу, которое равно 45 тыс. руб. Известные значения y- диапазон ячеек С37:N37, т.е. строка продажи. Известные значения х- диапазон ячеек С36:N36, т.е. строка расходы на рекламу. Нажимаем ОК. Получили значение 48,38413 млн. руб.
Литература
1. Приходько А.И. Практикум по эконометрике: Регрессионный анализ средствами Excel. Ростов на Дону: Феникс, 2007. 256 с. 2. Бараз В.Р. Корреляционно-регрессионный анализ связи показателей коммерческой деятельности с использованием программы Excel: учебное пособие. - Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. - 102 с.
ЦДТ "УНИВЕРМАГ", 1 ЭТАЖ
|

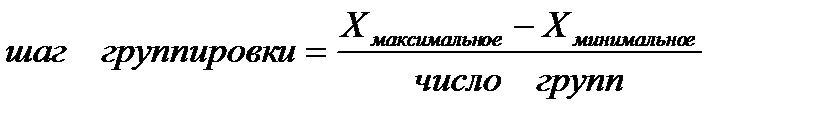

 - значение признака Y для i-й единицы в j_й группе;
- значение признака Y для i-й единицы в j_й группе; - значение признака Y в j-группе;
- значение признака Y в j-группе; - число единиц в j-й группе;
- число единиц в j-й группе;
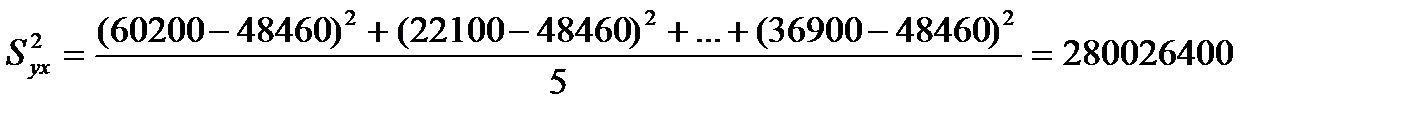
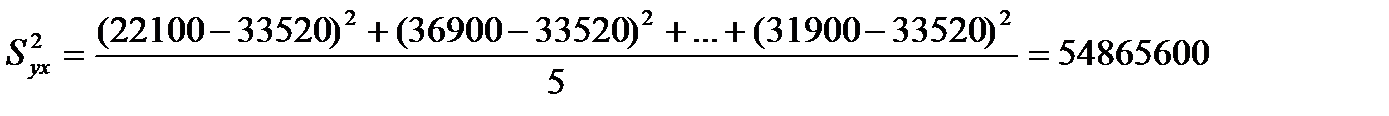

 =190388250
=190388250
 =38153010
=38153010
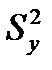 =228541260
=228541260 - коэффициент детерминации,
- коэффициент детерминации, = 0,833059
= 0,833059 - эмпирическое корреляционное отношение
- эмпирическое корреляционное отношение 0,91272, следовательно, имеется тесная связь между фактором и результативным показателем.
0,91272, следовательно, имеется тесная связь между фактором и результативным показателем.



 5, вызываем функцию “ЛГРФПРИБЛ”.
5, вызываем функцию “ЛГРФПРИБЛ”.
 =5,219798
=5,219798
 - коэффициент корреляции, вычисляемый с помощью функции "КОРРЕЛ".
- коэффициент корреляции, вычисляемый с помощью функции "КОРРЕЛ". - среднеквадратическое отклонение:
- среднеквадратическое отклонение: 





