Краткие сведения из теории. Критерии качества приема определяют правила, по которым работает приемник
Критерии качества приема определяют правила, по которым работает приемник. Правило может быть регулярным, если принятому сигналу Y(t) соответствует определенное решение λ¢ или сигнал S¢, или статистическим, если эта связь характеризуется определенной вероятностью. Мы будем рассматривать регулярное правило. Приемник, обеспечивающий минимальное различие принятого сообщения λ¢ (сигнал S¢) от переданного λ (сигнал S), называется оптимальным, или идеальным. Заметим, что здесь мы постоянно решение отождествляем с сигналом, так как между ними существует регулярная связь, и всегда λi соответствует сигнал Si. Далее возникает вопрос, как оценить различие между переданным сообщением λ и решением приемника λ¢ (или сигналами). Разумеется, здесь должны быть применены какие-то критерии. Критерий Котельникова (идеального наблюдателя) является самым распространенным в технике связи. Согласно ему решение должно выносится таким образом, чтобы суммарная вероятность ошибки была минимальная. Для оценки этого применяется условный статистический закон W(y/Si) принимаемого случайного сигнала y(t), который называется функцией правдоподобия. При гауссовской помехе эта функция имеет следующий вид:
где y – сигнал на входе демодулятора;
Если применить критерий Котельникова, выбор сигналов S0 и S1 идет по следующему правилу:
Поскольку функции правдоподобия нами найдены (2.1), то условие (2.3) при работе приемника будет таким:
Здесь необходимо сделать следующее замечание. Так как сигналы y и Si являются функциями времени, сравнение возможно произвести только в определенный момент времени t0. Такой метод называется приемом по одному отсчету. Вместо экспонент можно сравнивать их показатели и тогда
Если же усреднить по времени левую и правую части (2.5) и разделить на 2σ2, то неравенство принимает следующий вид:
где q(Si) – взаимная корреляция между принимаемым сигналом у и передаваемым Si, а ЕSi– энергия передаваемого сигнала. Если использовать значения входящих в (2.6) выражений q(Si) и ЕSi, то можно установить структурную схему оптимального приемника. Так как при непрерывной обработке
структура оптимального приемника должна содержать звенья, с помощью которых получается две функции (2.7) для каждого сигнала. Далее должно быть решающее устройство, которое определяет, по какой из ветвей обработки имеется максимальный результат, и тому сигналу отдается предпочтение в решении. Это положение иллюстрируется на рис. 2.1.
Рис. 2.1. Структурная схема оптимального приемника
Более определенный вид оптимального приемника будет зависеть от вида принятых сигналов. В качестве примера рассмотрим демодулятор амплитудно-модулированных сигналов: S0 = 0, S1 = A0×cos w0t (см. рис. 2.2).
В итоге получается так, что оптимальный приемник должен анализировать неравенство, которое следует из (2.6):
или
В результате анализа схема рис. 2.1 упрощается и принимает вид, показанный на рис. 2.3
Первые два блока приемника – это коррелятор; полученное значение взаимной корреляции сравнивается с порогом
Так как энергии сигналов равны (Е0 = Е1), то неравенство (2.6) упрощается и критерий проверки сводится к сравнению двух функций корреляции:
Смысл функции корреляции состоит в оценке статистической связи между сигналами. Естественно, с каким из двух сигналов «теснее» связан принимаемый сигнал, тому и должен отдать предпочтение приемник. На рис. 2.5 показана структурная схема оптимального приемника.
Вероятность ошибки как основная характеристика помехоустойчивости будет зависеть не только от интенсивности помех, но и от вида сигналов. Прежде чем сделать какое-то заключение, проведем анализ вероятности ошибки оптимального приемника. При определении вероятности ошибки примем допущение о том, что линия связи канала не дает искажений сигнала и имеет постоянные параметры передачи. Хотя природа сигнала, несущего информацию, случайна, будем считать, что он состоит из элементарных частиц – сигналов, имеющих детерминированный характер за время своего существования. Обратимся к неравенству (2.6) и перепишем его в ином виде:
 . (2.12) . (2.12)
В этом неравенстве есть случайные члены; их случайность определяется принимаемым сигналом у(t), в который входит помеха n(t). В то же время имеются и детерминированные члены – это энергии сигналов. Вынесем все случайные члены в одну часть неравенства, а детерминированные – в другую, тогда (2.12) приобретет следующий вид:
 , (2.13) , (2.13)
где Соотношение (2.13) следует понимать так: при передаче S0, если выполняется неравенство, приемник работает правильно, ошибок нет. Но если при передаче S0 неравенство будет развернуто в обратную сторону, приемник зафиксирует S1, и это будет ошибкой. Следовательно, вероятность ошибки Рош равна вероятности возникновения следующего неравенства:
 . (2.14) . (2.14)
Поскольку помеха носит аддитивный характер, то у(t) = Si(t) + n(t):
 . (2.15) . (2.15)
Перемножим выражения под интегралом и перенесем детерминированные члены в правую часть, тогда
 , (2.16) , (2.16)
где D S(t) = S0(t) – S1(t). Поскольку в левой части (2.16) присутствует случайная величина, а в правой – детерминированная, вероятность соблюдения данного неравенства можно найти обычным путем, если известен закон распределения случайной величины. Введем обозначения:
тогда вероятность ошибки где W(x) – закон распределения случайной величины. Случайная величина n(t)×DS(t) имеет нормальный закон распределения в силу того, что n(t) – гауссовская помеха [1.2]. Полученная в результате интегрирования величина x также имеет нормальный закон, ибо ему же подчиняются интегральные слагаемые:
В этом выражении пока неизвестна sx - среднеквадратическое отклонение величины
Рош = 1 – Ф(a), (2.19)
где Напомним, что функция интеграла вероятности Ф(a) приближается к единице с ростом аргумента a, поэтому вероятность погрешности тем меньше, чем больше a. Рассмотрим подробнее аргумент функции; для этого запишем его так:
где Еi – энергия сигнала. Из последнего выражения следует, что величина a зависит от отношения энергии сигналов к спектральной плотности мощности помехи или от отношения сигнал/помеха и, кроме того, зависит от значения интеграла
Если для связи выбран сигнал ЧМ (рис. 2.4), то
Так как Е0 = Е1 = Е, а соотношение частот w0 и w1 подобрано таким образом, что интеграл равен нулю (ортогональные сигналы), то
Полученное выражение в два раза больше, чем предыдущее, и вероятность ошибки при такой системе будет меньше. Если же выбрана система фазоманипулированных сигналов (ФМ) при фазовом сдвиге в 1800, то
Таким образом, здесь мы получили самую низкую вероятность ошибки. Система сигналов ОФМ занимает по вероятности ошибки промежуточное положение между ФМ и ЧМ. Заметим, что ЧМ-сигналы называются ортогональными, а ФМ – противоположными. Последнее название особенно ясно отражает их преимущество, поскольку этот термин означает, что сигналы значительно отличаются друг от друга и, следовательно, относительно легко различаются при приеме. Подробные сведения об оптимальных приемниках модулированных сигналов изложены в [1, с. 176 – 190; 2, с. 167 – 228; 3, с. 162 – 210; 4, с. 168 – 197].
|

 , (2.1)
, (2.1) – среднеквадратическое отклонение.
– среднеквадратическое отклонение.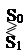

 . (2.2)
. (2.2) При равенстве априорных вероятностей p(S1) и p(S0) условие (2.2) будет несколько упрощено:
При равенстве априорных вероятностей p(S1) и p(S0) условие (2.2) будет несколько упрощено:
 . (2.3)
. (2.3)

 . (2.4)
. (2.4)

 . (2.5)
. (2.5)

 , (2.6)
, (2.6) , (2.7)
, (2.7)


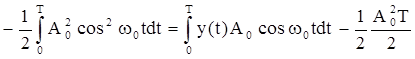 . (2.8)
. (2.8)
 0 (2.9)
0 (2.9)

 . (2.10)
. (2.10)

 ). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным.
). Такой способ приема сигналов при полностью известном передаваемом (а в приемнике – ожидаемом) сигнале называется когерентным. Разберем структуру частотного демодулятора: S0 = S×cоsw0t; S1 = S×cоsw1t (см. рис. 2.4).
Разберем структуру частотного демодулятора: S0 = S×cоsw0t; S1 = S×cоsw1t (см. рис. 2.4).
 . (2.11)
. (2.11) Таким образом, на этих двух примерах мы выяснили, что структура приемника зависит от системы применяемых сигналов. Но их вид в системе связи определяет не только это, но и помехоустойчивость связи. Различить при приеме два сигнала S0 = 1 В и S1 = 1,1 В приемнику сложнее, чем сигналы S1 = 1 В и S0 = -1 В.
Таким образом, на этих двух примерах мы выяснили, что структура приемника зависит от системы применяемых сигналов. Но их вид в системе связи определяет не только это, но и помехоустойчивость связи. Различить при приеме два сигнала S0 = 1 В и S1 = 1,1 В приемнику сложнее, чем сигналы S1 = 1 В и S0 = -1 В. ; i = 0, 1.
; i = 0, 1. ;
;  ,
,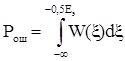 , (2.17)
, (2.17) . (2.18)
. (2.18) . Ее можно найти, усредняя по множеству x2. В результате получим
. Ее можно найти, усредняя по множеству x2. В результате получим 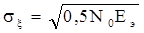 , где N0 – спектральная плотность мощности шума. Если теперь вернуться к (2.15), то интеграл может быть найден через специальные функции интеграла вероятности и
, где N0 – спектральная плотность мощности шума. Если теперь вернуться к (2.15), то интеграл может быть найден через специальные функции интеграла вероятности и ,
,  , х – переменная интегрирования.
, х – переменная интегрирования.

 , (2.20)
, (2.20) . Его смысл – взаимная корреляция между сигналами, применяемыми в системе. Следовательно, вид S0(t) и S1(t), степень их различия также влияют на вероятность ошибки. В качестве примера рассмотрим некоторые типы сигналов. Начнем с сигналов амплитудной модуляции (рис. 2.2). Найдем значение коэффициента a:
. Его смысл – взаимная корреляция между сигналами, применяемыми в системе. Следовательно, вид S0(t) и S1(t), степень их различия также влияют на вероятность ошибки. В качестве примера рассмотрим некоторые типы сигналов. Начнем с сигналов амплитудной модуляции (рис. 2.2). Найдем значение коэффициента a: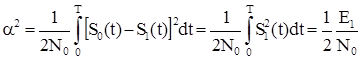 . (2.21)
. (2.21) . (2.22)
. (2.22) . (2.23)
. (2.23) , а коэффициент
, а коэффициент  .
.


