Краткие сведения из теории. Известное представление сигналов ортогональными рядами может получить геометрическую трактовку
Известное представление сигналов ортогональными рядами может получить геометрическую трактовку. Так, например,
Рис. 1.1. Векторное представление гармонических сигналов
Найдем расстояние d между концами векторов, воспользовавшись правилами тригонометрии:
Чем больше d, тем выше помехоустойчивость системы связи. Определяется она как нормами самих сигналов, так и произведением
Представив произведение синусов через косинусы разности и суммы аргументов, получим
Второй интеграл от знакопеременной функции имеет нулевое решение, а первый равен
Мы получили известное выражение скалярного произведения и это дает основание утверждать, что в общем виде для любых сигналов оно будет равно
Свойство ортогональности сигналов заключается в том, что их скалярное произведение равно нулю. Естественно, такие сигналы получили название ортогональных. Данное свойство способствует лучшему распознаванию сигналов и увеличению отношения сигнал/помеха и поэтому используется при построении схем приемников. Поясним это утверждение подробнее. Допустим, в составе приемника имеется схема, вычисляющая скалярное произведение. Как и прежде, будем считать сигналы гармоническими. Что же дает такая обработка?
В общем случае приемник – демодулятор состоит из двух блоков: УОО – устройства оптимальной обработки и РУ – решающего устройства (рис. 1.2).
Рис.1.2. Состав приемника
Назначение УОО заключается в повышении отношения сигнал/помеха. Его схема часто дополняется входным узкополосным фильтром для отстройки от помех, сосредоточенных по спектру сигнала. Поэтому если помеха на входе случайна и широкополосна (белый шум), то на выходе фильтра будет узкополосное случайное воздействие, которое можно записать так: В результате скалярной обработки при опорном сигнале
Воспользовавшись известными формулами тригонометрии и учитывая, что интегралы от произведения знакопеременных функций синуса и косинуса равны нулю, получим результат
|

 , где
, где  – координаты вектора сигнала в m - мерном пространстве, а
– координаты вектора сигнала в m - мерном пространстве, а  – параметры сигнала. Разберем пример с двумя гармоническими сигналами
– параметры сигнала. Разберем пример с двумя гармоническими сигналами  и
и  , имеющими длительность T, кратную периоду колебаний. Так как сигналы меняются во времени, найдем их усредненные значения - нормы:
, имеющими длительность T, кратную периоду колебаний. Так как сигналы меняются во времени, найдем их усредненные значения - нормы:  , тогда
, тогда  и
и  . Изобразим векторы сигналов S0 и S1 с нормами
. Изобразим векторы сигналов S0 и S1 с нормами  и
и  в декартовой системе координат. Очевидно, что векторы будут отличаться друг от друга величиной и фазой (рис.1.1).
в декартовой системе координат. Очевидно, что векторы будут отличаться друг от друга величиной и фазой (рис.1.1).
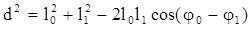 . (1.1)
. (1.1)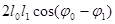 , получившим название скалярного. Обобщим это понятие на сигналы любого вида. Для этого найдем решение интеграла от произведения двух ранее принятых гармонических сигналов:
, получившим название скалярного. Обобщим это понятие на сигналы любого вида. Для этого найдем решение интеграла от произведения двух ранее принятых гармонических сигналов: . (1.2)
. (1.2) . (1.3)
. (1.3)
 . (1.4)
. (1.4) . (1.5)
. (1.5)
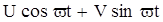 . Это сумма синфазной и квадратурной составляющих помехи.
. Это сумма синфазной и квадратурной составляющих помехи. имеем:
имеем: (1.6)
(1.6) . Таким образом, синфазная составляющая помехи будет равна нулю, и в итоге повышается соотношение сигнал/помеха. Основные сведения о свойстве ортогональности приведены в [1, с. 44 – 45; 2, с. 51; 3, с. 36 – 37]
. Таким образом, синфазная составляющая помехи будет равна нулю, и в итоге повышается соотношение сигнал/помеха. Основные сведения о свойстве ортогональности приведены в [1, с. 44 – 45; 2, с. 51; 3, с. 36 – 37]


