В.А.Гришанов, Н.А.Дроздов
Лабораторная работа №5.
Цель работы: знакомство с методикой определения основных характеристик неравновесных носителей заряда, определение lD и t для различных полупроводниковых материалов, приобретение навыков работы с современной электронной аппаратурой.
ВВЕДЕНИЕ
При возбуждении (например, освещении) полупроводника концентрация свободных электронов и дырок в нём (n и p) превышает равновесную концентрацию (n0 и p0), что приводит к увеличению проводимости полупроводника. Электроны и дырки проводимости, не находящиеся в термодинамическом равновесии, называются неравновесными носителями заряда (ННЗ). После прекращения освещения избыточные концентрации носителей заряда (например, Dn = n – n0) стремится к нулю в результате процесса рекомбинации. Скорость уменьшения концентрации ННЗ dn/dt, т.е. скорость рекомбинации, характеризуется величиной t, называемой временем жизни ННЗ. В простейшем случае (т.н. линейной рекомбинации) спад концентрации ННЗ во времени вследствие рекомбинации подчиняется экспоненциальному закону: Dn = Dn(0)exp(–t/t) (1) Помимо времени жизни явление рекомбинации можно характеризовать диффузионной длиной lD. Эта величина, по определению, представляет собой расстояние, на котором концентрация ННЗ уменьшается в е раз. Если генерация ННЗ будет иметь место лишь в малой области кристалла (освещение узкой полоской света), то в этой области концентрация их будет выше чем в остальных точках кристалла. Под влиянием градиента концентрации Dn/Dx = (n – n0)/ Dx начнется диффузия избыточных носителей заряда из области их генерации. Очевидно, что путь lD, который пройдут в кристалле носители, определяется их временем жизни, ибо в конце его избыточные носители рекомбинируют, и подвижностью, так как рассеяние затрудняет перемещение носителей. В результате между lD и t имеет место следующее соотношение:
где D – коэффициент диффузии носителей заряда. В свою очередь, величина D определяется выражением, известным под названием соотношения Эйнштейна:
где m – подвижность электронов или дырок; k – постоянная Больцмана; е – заряд электрона; Т – температура. Величины lD и t являются важнейшими паспортными данными полупроводникового материала. Они определяются параметрами кристаллической решётки и зонной структурой конкретного полупроводника и, кроме того, наличием примесей и дефектов в кристалле.
ТЕОРИЯ Основными уравнениями, описывающими поведение ННЗ, являются: 1. Уравнения для плотностей тока электронов и дырок
где Dn, Dp, mn, mp – соответственно, коэффициенты диффузии и подвижности электронов и дырок; Е – напряжённость электрического поля. 2. Уравнения непрерывности, с учётом генерации и рекомбинации ННЗ:
где gn, gp – скорости генерации, a tn, tp – времена жизни электронов и дырок. 3. Уравнение Пуассона
где r – суммарный заряд примесей и носителей заряда; j – потенциал. В подавляющем большинстве случаев при рассмотрении процессов, связанных с ННЗ, пренебрегают возникающим пространственным зарядом и уравнение (6) заменяют условиями нейтральности
где mi, mi0 – неравновесная и равновесная концентрация электронов на уровнях i-го сорта в запрещённой зоне полупроводника. При подстановке (4) в (5) и при учете (7) задача о поведении ННЗ обычно сводится к решению уравнений непрерывности в частных производных:
Рассмотрим одномерный случай задачи, показанный на рис.1. Такая ситуация может быть реализована при использовании в эксперименте длинных образцов, засвечиваемых узкой поперечной полоской света. Решение уравнения (8) для этого случая приведено в [1]. С учётом граничных условий: равенства нулю концентраций ННЗ при x®±¥; а также условия конечности и непрерывности потока частиц на границах областей при x = 0 и x = –L, решение системы (4), (5), (7) имеет вид: для области 1:
для области 2:
для области 3:
где
и
В отсутствие электрического поля, т.е. при lE = tmE = 0, когда имеет место только диффузия, из (11) и (12) получаем: l1 = l2 = lD Это соотношение позволяет сравнительно просто определять величину lD. Плоская поверхность образца освещается узкой полоской света. На некотором расстоянии от освещенного места находится точечный зонд-коллектор, на который подано запирающее напряжение. Ток в цепи коллектора прямо пропорционален концентрации ННЗ. Изменяя расстояние между коллектором и освещаемой областью, находят зависимость Dn = f(x), которая в логарифмическом масштабе имеет вид прямых с наклоном 1/ lD. Величина t может быть найдена после этого из формулы (2). В 1954 году Г.Адамом была предложена модификация описанного выше способа, согласно которой возможно раздельное определение времени жизни и длины диффузии ННЗ. Согласно этому методу на исследуемый образец падает узкий луч света, движущийся по его поверхности с постоянной скоростью. Генерируемые в освещённой части образца ННЗ диффундируют из неё в неосвещённые области. Вследствие движения светового луча пространственное распределение носителей заряда перемещается по образцу вместе с ним. Рассмотрим решение системы уравнений (4), (5), (7) для этого случая. Подставляя (5) в (4) и переходя к системе координат, движущейся вместе с областью генерации, получаем
Формулы, связывающие переменные в неподвижной и подвижной системах координат, имеют следующий вид
В системе координат, движущейся вместе со световым лучом, распределение ННЗ стационарное, тогда
Это уравнение по форме совпадает с (8). Решение его по аналогии с (9) и (10) имеет вид
где
для области 2
где
Вернёмся к старым переменным:
Нас интересует концентрация ННЗ в фиксированной точке, соответствующей месту установки коллектора
где
Для области 2
где
Таким образом, сигнал на коллекторе при равномерном движении области возбуждения состоит из двух экспоненциальных ветвей с разными постоянными времени, определяемыми выражениями (23) и (25) и переходной области, выражение для которой мы писать не будем. При отсутствии электрического поля выражения (23), (25) примут вид
Из выражений (26) и (27) легко получаются формулы для t и D.
МЕТОД ИССЛЕДОВАНИЯ
Измерение времени жизни и длины диффузии ННЗ методом движущегося светового зонда производят с помощью установки, показанной на рис. 2.
Свет гелий-неонового лазера (1), l = 0,63 мкм, с помощью цилиндрической линзы (3) фокусируется на поверхности образца (5) в виде узкой полоски. Движение области возбуждения вдоль образца обеспечивается за счёт вращения зеркала (4), установленного на оси электродвигателя с регулируемой скоростью вращения. Сигнал фото-э.д.с., пропорциональный фототоку образца, а, следовательно, концентрации ННЗ в области зонда-коллектора (6), подаётся на вход “у” осциллографа. Запуск развёртки осциллографа осуществляется от опорного фотодиода (7). Наблюдаемый на экране осциллографа сигнал представляет собой зависимость концентрации ННЗ от времени в точке контакта измерительного зонда (рис. 3). Точки экспоненциальных спадающих участков кривой в полулогарифмическом масштабе укладываются на две прямые линии с различными наклонами
При движении светового луча к коллектору
При движении светового луча от коллектора
Определения t и D производится затем по формулам (28) и (29). С помощью переключателя (9) на вход “у” осциллографа вместо сигнала с образца могут подаваться сигналы двух фотодиодов, расстояние между которыми равно 40 мм. В этом режиме осуществляется измерение скорости движения светового луча по образцу. Для улучшения качества выпрямляющего контакта зонда-коллектора предусмотрен режим формовки контакта. В этом режиме через контакт производится разряд конденсатора ёмкостью 1 мкФ, заряженного до напряжения 300 В.
|

 (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) , (7)
, (7) (8)
(8)
 (9)
(9) (10)
(10) (11)
(11) (12)
(12) ;
;  (13)
(13) (14)
(14) ;
;  (15)
(15) и (14) примет вид
и (14) примет вид (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) . Тогда в области 1
. Тогда в области 1 (21)
(21) (22)
(22) (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28) (29)
(29)
 и
и 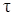
 и
и  согласно (26) и (27).
согласно (26) и (27).
 (30)
(30) (31)
(31)


