Испарение нефтепродуктов в атмосферу
В сосуде с открытой поверхностью (рис. 1.3.1) испаряющейся жидкости концентрация пара в вертикальном направлении изменяется по кривой от значения насыщенной концентрации Cs у поверхности жидкости до нуля на определенном расстоянии от нее. В дальнейшем принято допущение, что рассеивание паров жидкости за пределы вертикального столба над поверхностью резервуара отсутствует. Кривая изменения концентрации паров имеет вид:
где a, b – константы; y – координата точки, в которой определяется концентрация паров жидкости; С(y) – концентрация пара в рассматриваемой точке y. Константы a и b могут быть определены из граничных условий: при y=0, в точке с нулевым значением концентрации, C(0) = 0, следовательно b=0, при y = x, непосредственно у поверхности жидкости, C(y) = Cs, следовательно:
Подставив значения констант в (1.3.1), получим:
Средняя концентрация паров Сср будет равна:
Рис. 1.3.1. Координатная система определения концентрации паров испаряющейся жидкости. Таким образом, при известном расстоянии х и известном показателе степени n, можно определить как среднюю концентрацию, так и концентрацию пара нефтепродукта в любой точке по высоте над испаряющейся жидкостью. Естественно, что расстояние х изменяется для каждого продукта в зависимости от длительности испарения и температуры. Чтобы связать концентрацию паров C(y,t) с расстоянием х и временем испарения t, составим дифференциальное уравнение материального баланса, в предположении, что все пары нефтепродукта находятся в вертикальном объеме столба воздуха площадью F, равной площади испарения (сосуда):
где Gи - масса испарившейся жидкости, GА - масса паров, находящихся (аккумулированных) в воздухе. Массу испаряющейся со свободной поверхности жидкости можно определить на основании закона Фика с учетом поправки Стефана на конвективную диффузию:
где D - коэффициент диффузии паров нефтепродукта в воздухе с поправкой на температуру,
Значение градиента концентрации можно получить, если продифференцировать уравнение (1.3.2):
Непосредственно на поверхности жидкости (при y = x) это уравнение принимает вид:
После подстановки (1.3.7) в (1.3.5) получим:
Масса GA паров жидкости, находящихся в воздухе, может быть вычислена с учетом предположения, что при изменении времени на dt будет изменяться только высота зоны распространения паров на величину dx. Тогда, с учетом (1.3.3), получим:
где Vx - объем, занимаемый парами нефтепродукта. Подставив (1.3.9) и (1.3.8) в уравнение (1.3.4) и проинтегрировав его в предположении, что при изменении времени от 0 до t высота зоны паров меняется от 0 до х, получим:
Разрешив уравнение (1.3.12) относительно х, найдем расстояние от поверхности жидкости до плоскости, где концентрация паров испаряющегося нефтепродукта будет равна нулю:
Подставив найденное значение х в выражение (6.9.2), получим уравнение для определения концентрации пара в любой плоскости над поверхностью жидкости в зависимости от продолжительности испарения:
Рис. 1.3.2. Изменение процесса испарения во времени, связанное со смещением начала координат функции изменения концентрации паров по высоте столба паровоздушной смеси в разные моменты времени (t2 > t1). При исследовании испаряемости нефтепродуктов установлено, что показатель степени n кривой изменения концентрации паров при испарении в условиях молекулярной диффузии колеблется около значения 2.
Тогда из уравнения (1.3.13):
Аналогично, из уравнения (1.3.14), имеем:
где y - интересующее расстояние над поверхностью испаряющейся жидкости, м; х - расстояние от поверхности нефтепродукта по вертикали до плоскости, где концентрация паров равна нулю, м; D - коэффициент диффузии с поправкой на температуру, м2/с; СS - концентрация насыщенных паров при данной температуре нефтепродукта, объемн. доли. Чтобы определить высоту зоны взрывоопасности над поверхностью испаряющегося нефтепродукта х0, достаточно, задать длительность испарения и принять опасную концентрацию в виде:
где С0 - опасная концентрация паров, объемн. доли;k < 1 - коэффициент безопасности, учитывающий возможные методические неточности и неточности исходных данных. Определяя значение y из, получим:
Массу нефтепродукта, находящегося в неподвижном воздухе высотой х за любой промежуток времени можно определить, подставив найденное значение х из (1.3.15) в формулу (1.3.9):
где GИ - масса нефтепродукта, находящегося при нормальном давлении и температуре Т в зоне испарения высотой х;
|

 (1.3.1)
(1.3.1) , где Cs – концентрация насыщенных паров рассматриваемой жидкости.
, где Cs – концентрация насыщенных паров рассматриваемой жидкости. , (1.3.2).
, (1.3.2). (1.3.3).
(1.3.3).
 (1.3.4),
(1.3.4),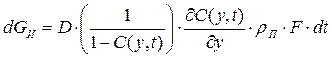 (1.3.5),
(1.3.5), - градиент концентрации паров по вертикали (частная производная по координате y), rП - плотность паров нефтепродукта.
- градиент концентрации паров по вертикали (частная производная по координате y), rП - плотность паров нефтепродукта.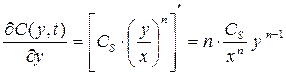 (1.3.6).
(1.3.6). (1.3.7).
(1.3.7). (1.3.8)
(1.3.8) (1.3.9)
(1.3.9) (1.3.10)
(1.3.10) (1.3.11)
(1.3.11) (1.3.12)
(1.3.12) (1.3.13)
(1.3.13) (1.3.14).
(1.3.14).
 (1.3.15).
(1.3.15). (1.3.16),
(1.3.16), (1.3.17),
(1.3.17), (1.3.18)
(1.3.18) (1.3.19),
(1.3.19), - плотность паров нефтепродукта, кг/м3, вычисленная для нормального атмосферного давления при температуре 0°С (273.15 К); МП×10 -3 - молярная масса нефтепродукта, кг/моль; Т – температура среды, К; Т0 = 237.16 К; VA = 22.4×10 -3 м3/моль - объем, занимаемый одним молем идеального газа при нормальном давлении и температуре.
- плотность паров нефтепродукта, кг/м3, вычисленная для нормального атмосферного давления при температуре 0°С (273.15 К); МП×10 -3 - молярная масса нефтепродукта, кг/моль; Т – температура среды, К; Т0 = 237.16 К; VA = 22.4×10 -3 м3/моль - объем, занимаемый одним молем идеального газа при нормальном давлении и температуре.


