Часть 2. Пылинка, имеющая массу 10-8г и заряд
(-1,8)·10-14Кл, влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между его пластинами (см. рисунок, вид сверху). Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.
Вариант №1
В1. В доме, в котором живет Оля, 9 этажей и несколько подъездов. На каждом этаже находится по 6 квартир. Оля живет в квартире №98. В каком подъезде живет Оля? В2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.
В3. Найдите площадь треугольника, вершины которого имеют координаты (1;7), (3;7), (7;9).
В4. В таблице даны тарифы на услуги трех фирм такси. Предполагается поездка длительностью 70 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?
*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки. В5. Найдите корень уравнения В6. В треугольнике ABC AC=20, BC =4,5,, угол C равен 900. Найдите радиус вписанной окружности.
В7. Найдите значение выражения В8. На рисунке изображен график
В9. В правильной шестиугольной призме В10. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет все три раз В11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара. В12. Высота над землeй подброшенного вверх мяча меняется по закону В13. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? В14. Найдите наименьшее значение функции Часть 2
С1 а) Решить уравнение 4 s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/></w:rPr><m:t>sin</m:t></m:r></m:fName><m:e><m:r><m:rPr><m:sty m:val="bi"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/></w:rPr><m:t>x</m:t></m:r></m:e></m:func></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> б) Указать корни, принадлежащие промежутку С2. В правильной шестиугольной призме ABCDEFA1 B1 C1 D1 E1 F1 все ребра которой равны 10, найдите расстояние от точки Е до прямой В1 С1 С3. Решить систему неравенств
С4. Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 40, а отношение катетов треугольника равно С5. Найти все значения а, при каждом из которых наименьшее значение функции f(x) = 2 a x + С6. Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1008 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Вариант №2 Часть 1
В1. В сентябре 1 кг картофеля стоил 20 рублей, в октябре картофель подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг картофеля после подорожания в ноябре? В2. На рисунке жирными точками показан курс доллара, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какой был курс доллара 9 октября. Ответ дайте в рублях.
В3. Найдите площадь прямоугольника, вершины которого имеют координаты (9;0), (10;1), (1;10), (0;9).
В4. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 36 км/ч, через пункт С едет автобус со средней скоростью 48 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 56 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам. Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
В5. Найдите корень уравнения В6. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 800. Найдите n. В7. Найдите значение выражения В8. На рисунке изображен график
В9. Найдите квадрат расстояния между вершинами
В10. В среднем из 1500 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. В11. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра. В12. Расстояние от наблюдателя, находящегося на небольшой высоте В13. Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс? В14. Найдите наименьшее значение функции
|

 Пылинка, имеющая массу 10-8г и заряд
Пылинка, имеющая массу 10-8г и заряд



 .
. — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек экстремума функции
. Найдите количество точек экстремума функции  .
.
 все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?
, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров? на отрезке
на отрезке 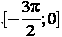 .
. +5 = 0.
+5 = 0. .
.
 .
. больше 1.
больше 1.


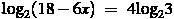 .
. .
. . Найдите промежутки убывания функции
. Найдите промежутки убывания функции 
 и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
 километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле
километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле  , где
, где  (км) — радиус Земли. С какой высоты горизонт виден на расстоянии восемь километров? Ответ выразите в километрах.
(км) — радиус Земли. С какой высоты горизонт виден на расстоянии восемь километров? Ответ выразите в километрах. на отрезке
на отрезке  .
.


