А. М. ВАСИЛЬЕВ
1-я типография Профиздата, Москва, Крутицкий вал, 18 Волновые функции, которые дают описание распространяющихся в пространстве возмущений физических величин, могут быть получены как решения специфических дифференциальных уравнений, называемых волновыми уравнениями. Вид уравнения зависит от рассматриваемой физической системы, её геометрии и того параметра, который испытывает возмущение. Само волновое уравнение можно получить исходя из основополагающих физических законов. Например, применяя законы динамики к струне или стержню, получают волновоеуравнение для механических волн. Изучая упругие свойствагаза изаконы термодинамики, получают волновое уравнениедля звуковых волн. Система уравнений Максвелла приводитк волновому уравнению для электромагнитных волн. Методыполучения и решения волновых уравнений сложны. Мыможем познакомиться только с некоторыми простейшими результатами. Изучение динамики и термодинамики газа приводит к уравнению

Это разные формы записи одного и того же дифференциального уравнения относительно неизвестной волновой функции и=и(х,t), представляющей собой величину, на которую изменяется среднее давление газа в точке
где р - среднее давление газа, χ=cp/cv- показатель адиабаты, ср и с v - теплоёмкости при постоянном давлении и постоянном объёме, T- абсолютная температура,B=R/μ - удельная газовая постоянная. Решением уравнения (1) служит плоская волна. Если геометрия системы иная, то волновое уравнение может приобрести вид
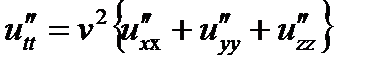
Волновое уравнение может иметь ещё более общую форму. Уравнения Максвелла позволяют получить волновое уравнение для электрической и магнитной составляющих электромагнитной волны. В вакууме эти уравнения имеют вид
где с - скорость света, а векторная волновая функция Для смещения струны или стержня можно получить уравнения типа (4), которые содержат квадрат скорости механических волн
 где T=F / S - натяжение струны, S - площадь её поперечного сечения, Е - модуль упругости стержня, ρ- объёмная плотность вещества. Подчеркнём, что в уравнениях (1) и (3) волновые функции связаны с изменением скалярного параметра (давления) и скалярны, тогда как в уравнениях (4) волновые функции имеют векторную природу.

Векторные волновые функции характеризуются направлением поляризации или поляризацией. Вектор поляризации определяется дробью
В простых физических системах вектор Если вектор Волны смещения на струне поперечны. В стержнях обычно изучают продольные волны смещения. Свободные ЭМ-волны в вакууме поперечны. ЗАДАЧА 1. Записать волновую функцию продольной монохроматической волны, циклическая частота которой ω, а волновой вектор равен По условию волна плоская (задан волновой вектор к) и продольная, т.е. векторная. Вектор поляризации продольной волны
ЗАДАЧА 2. Записать волновую функцию поперечной монохроматической волны, распространяющейся вдоль оси.у.' Условие поперечности волны в данном случае имеет вид
Заметим, что вектор
ЗАДАЧА 3. Записать волновую функцию продольной сферической волны, источник которой находится в начале координат. В любой точке пространства сферическая волна распространяется вдоль радиус-вектор
считать, что волна монохроматическая, то ЗАДАЧА 4. Проверить, что скалярная волновая функция и = и0 cosφ;,φ=ωt-кх, является решением уравнения волнового уравнения (1), если v=ω/k. Для решения задачи найдём частные производные функции u(x,t).
 (7) (7)
а dt ЗАДАЧА 5. Проверить, что
Вынесем вектор
Воспользуемся правилами дифференцирования сложных функций. Тогда
Отсюда следует, что
И Подставив (11) и (12) в (10), получим тождество. Задача решена. ТЕМА 3. СЛОЖЕНИЕ ВОЛН Обычно под волнами подразумевают небольшие возмущения параметров, характеризующих систему. Например, при распространении звука связанное с ним изменение давления u(
Уравнение (1) является линейным дифференциальным уравнением. Важное свойство подобных уравнений формулируется так: если и1 и и2 есть решения (1), то их сумма также является его решением, u(x,t)= u1 (x,t) + u2(x,t). (2) Свойство (2) известно, как принцип суперпозиции волн. Он утверждает, что волны распространяются в среде независимо, не влияя друг на друга. Это следствие малости возмущения параметров физической системы. Те системы, для которых такое приближение оправдано, называются линейными. Но в некоторых случаях среда сильно реагирует на возмущения, связанные с волной. Тогда приходится учитывать влияние изменений, вызванных волной, на условия распространения этой и других волн. Среда перестаёт быть линейной. В нелинейных средах волновое уравнение теряет линейность и принцип суперпозиции нарушается. Тогда волны уже не могут рассматриваться независимо и влияют друг на друга через вызванное ими изменение свойств среды. Наложение волн друг на друга приводит к важным следствиям даже в линейных средах. Например, две одинаковые волны, идущие навстречу друг другу перестают переносить энергию (очевидный факт). Примером таких волн может служить набор u1=u0cosφ1, φ1=ωt-kx+φ0, u2=u0cosφ2, φ2=ωt-kx+φ0 (3) Сложив их согласно принципу (2), получим результирующую волну
Это стоячая волна. Точки хп, в которых cos k хn=0 (и вся волновая функция равна нулю), неподвижны. Они называются узлами. Легко найти
координаты узлов, потребовав k хn = π;(2n+1)/2. Т огда хn = π;(2n+1)/(k2),причём n - любое целое число. Между узлами расположены пучности стоячей волны, где coskхn =
Часто приходится складывать не две, а большее число волн. Для этого разработан удобный “Метод векторных диаграмм”. Познакомимся с этим методом, рассматривая монохроматическую волну u = и0 cosφ, φ = ωt- кх+φ0. В любой момент времени волна характеризуется двумя величинами - амплитудой и0 и фазой (углом) φ. Пара величин (и0,φ) изображается точкой А на полярной диаграмме или в полярной системе координат. Значит, волне и можно сопоставить вектор Если имеется, например, три волны и1, и2, и3 (они должны распространяться в одном направлении и иметь одинаковые поляризации), то им соответствуют три вектора ЗАДАЧА 1. Пусть волновое уравнение
Если учесть (7), (8) и (9), то из (5) следует
Или Если учесть (6), то окажется, что скобка в (10) должна равняться нулю. Но и в общем случае, это не выполняется. Следовательно, предположение (7) ошибочно, а это означает, что принцип суперпозиции в данном случае не выполняется. ЗАДАЧА 2. Найти длину стоячей волны λст, если образующие её бегущие волны имеют длину волны λ. Длина стоячей волны - это расстояние между двумя соседними узлами или пучностями. Координаты пучностей определяются условием coskхт= ±1. Отсюда k хт= πт, т - целое число, и хт= тπ/к. Значит,
ЗАДАЧА 3. Используя метод векторных диаграмм, сложить волны u1 = 3 cos φ1, и2 = 2cosφ2, иЗ = 3 cos φ3, у которых в данный момент времени и в данной точке фазы равны φ1= 0, φ2= π /2, φ3= π. Волны идут в одном и том же направлении. В методе векторных диаграмм этим волнам соответствуют три вектора
Сложив их по методу треугольников, получим результирующий вектоh ЗАДАЧА 4. Используя метод векторных диаграмм, сложить векторные волны Векторный характер волн не изменяет приведённого выше решения. Модуль амплитуды результирующей волны |
ТЕМА 4. ИНТЕРФЕРЕНЦИЯ ВОЛН Энергетической характеристикой волны является интенсивность. Размерность интенсивности равна Дж/(м 2 *с) или Вт/м2, т.е. интенсивность представляет собой численное значение плотности потока энергии, переносимой волной. Интенсивность - это энергия, падающая на единичную площадку за единицу времени. Мгновенной интенсивностью называют величину
где коэффициент, согласующий размерности Обычно рассматривают интенсивность, среднюю за какой-либо интервал времени. Согласно определению, среднее за время τ есть
Если в линейных средах волновые функции подчиняются принципу суперпозиции, т.е. результирующая волна равна
то интенсивность таким свойством не обладает. Найдём интенсивность волны (3):
Видно, что интенсивность Формулы (3) и (4) приведены для скалярных волн. Для векторных волн (4) изменяется так, что появляется cos β, β;- угол между направлениями поляризации волн:
Если волны поляризованы ортогонально, то косинус угла β;обращается в нуль и интерференционный член пропадает. Ортогонально-поляризованные волны никогда не интерферируют. Другое требование, необходимое для наблюдения интерференции волн, связано с их когерентностью. В простейшем понимании когерентность - это согласованность волн. Принято выделять три режима наб-
1. Низкочастотные волны. Если складываются две монохроматические волны
и оказывается, что 2. Высокочастотные волны. Случай 1. Если мгновенные значения интерференционного слагаемого и воспринимает только средние значения интенсивности. Величина интерференционного слагаемого равна Интеграл с φ1+φ2 не представляет интереса, так как за время τ подынтегральная функция многократно изменяет свой знак и обращает весь интеграл в нуль. В интеграле с φ1-φ2 возможен случай, когда |ω1-ω2|τ<<1 (8) Тогда подынтегральная функция может считаться постоянной и после ее вынесения из-под знака интеграла интерференционный член равняется I12=αu01u02cos(φ1-φ2) (9) (фазы берут в произвольный момент времени Волны, для которых справедливо условие (8), называется достаточно когерентными для наблюдения их интерференции данным прибором. 3. Высокочастотные волны. Случай 2. Если вместо (8) имеет место неравенство ЗАДАЧА 1. Найти интерференционные слагаемые, возникающие при наложении трёх волн
Имеем простейший случай многолучевой интерференции. Полная интенсивность суммарной волны равна (для простоты считаем а=1)
Видно, что выделяются три интерференционных слагаемых, которые 2
Пусть рассматриваются волны β- угол между поляризациями волн. Заметим, что и1и2 = const*(cos (φ1+φ2)) + cos(φ1-φ2)). Первое слагаемое высокочастотное и его вклад в интерференционное слагаемое не наблюдаем. Второе
даёт искомый ответ. Оно не зависит от времени и не изменяется при
При этом интерференционное слагаемое равно
Высокочастотный вклад обращается в нуль в силу периодичности косинуса. Низкочастотный вклад с φ1-φ2 не зависит от времени и после усреднения равен
Итак,
Максимумы интерференционной картины образуются, когда Δφ=2πm, т.е. когда
ТЕМА 5. ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. ДИФРАКЦИЯ
Дифракция - это огибание волнами малых препятствий, т.е. нарушение закона прямолинейного распространения волн. Френель дополнил принцип Гюйгенса, заметив, что фиктивные источники когерентны и создаваемые ими вторичные волны интерферируют. Принцип Гюйгенса-Френеля утверждает: в любой точке вне замкнутой поверхности, охватывающей источник волны, волну можно представить как результат наложения интерферирующих вторичных волн, которые возбуждаются фиктивными источниками, равномерно распределёнными по рассматриваемой вспомогательной поверхности. На основании принципа Гюйгенса-Френеля дают “широкое” определение дифракции. Дифракция - это комплекс явлений, происходящих с интерферирующими вторичными волнами, распространяющимися в средах с резкими неоднородностями. Комплекс явлений учитывает: 1) нарушение закона прямолинейного распространения волн; 2) перераспределение интенсивности падающей волны и возникновение интерференционных максимумов и минимумов; 3) возникновение многолучевой интерференции волн, идущих от фиктивных источников; 4) разный характер дифракции на разных расстояниях от препятствия; 5) возможность того, что неоднородности могут быть амплитудными (непрозрачные экраны) и фазовыми (прозрачная среда с резкими скачками коэффициента преломления).
Для математического описания дифракции Френель предложил метод разбиения вспомогательной поверхности на области, расстояния от границ которых до точки наблюдения различаются на λ/2. Френель предложил: 1. Для точечного источника S брать сферическую вспомогательную поверхность F. благодаря чему все фиктивные источники будут когерентны и синфазны (т.е. иметь одинаковые начальные фазы). 2. Разбивая поверхность F на кольца так, чтобы расстояния от соседних колец до точки наблюдения Р отличались на λ/2 Площадь колец в методе Френеля равна S=πλab/(a+b) (1) Метод Френеля применим к волнам любой физической природы и будет использован для решения осесимметричных дифракционных задач. Для качественной характеристики дифракционных явлений важен волновой параметр
λ; - длина волны, r- расстояние от препятствия до точки наблюдения, d - характерный размер препятствия (ширина щели, нити, т.д.). Если Р<< 1, то дифракционные эффекты незаметны. Это область параметров, при которых волна распространяется прямолинейно, т.е. область геометрической оптики. Если Р~1, то фазовая поверхность заметно искажена и прямолинейность распространения волны нарушена. Это область дифракции Френеля. Если Р>>1, то точка наблюдения считается бесконечно удалённой. Волну можно считать плоской. Возникает дифракция Фраунгофера или дифракция плоских волн. ЗАДАЧА 1. Используя принцип Гюйгенса, построить фазовую поверхность плоской волны, отражающейся от зеркала.
Через время t1 точка b1 совпадает с поверхностью зеркала, становясь фиктивным источником. За это время фазовая поверхность волны отойдёт от источника а1 на расстояние ct1. Огибающая будет иметь вид прямой a2b2. Фазовая поверхность испытает излом и займёт положение 2. Ещё через время t2 на зеркало попадёт точка с1, радиус фазовой поверхности волны, испущеной точкой а1, станет равным ct2, а поверхность волны, испущенной источником в точке b2-c(t2-t2). Волновая поверхность займёт положение 1У и произойдёт полное отражение рассматриваемой части плоской волны. Заметим, что точка a, находившаяся на фазовой поверхности “слева”, теперь лежит “справа”. Строя огибающую, можно доказать, что угол падения волны равен углу отражения.
того, SO = SB = a, РО = b, АО = x,АВ = r. По теореме Пифагора (РВ)2=(АВ)2+(АР)2 и (SB)2 =(AB)2+(SA)2 (3) т.е. r2=(b + (1/2)λk)2-(b+x)2 и r2 = а2 - (а - х) 2. (4) Считая, что λ;k<<ab и пренебрегая квадратом (λr)2, находим xk= bλ k[2(а + b)], (5) поэтому площадь k-го кольца есть Sk = 2π a[xk+i - хk] = π ab/(a + b) λ. (6) ЗАДАЧА 3. Наблюдение дифракции проводится на расстоянии r =2 м от экрана со щелью шириной d =10 мкм. Длина волны λ;=2мкм. Какой тип дифракции наблюдается? Характер дифракции определяется волновым параметром (2), Данные условия задачи приводят к значению Р = 200 >> 1. Это условие наблюдения дифракции Фраунгофера / дифракции плоских волн /. ЗАДАЧА 4. Свет с λ; = о ,5 мкм падает на длинную линейку, ширина которой d = 2 см. На каком расстоянии от линейки дифракционными явлениями можно пренебречь? Дифракционные явления незаметны в области геометрической оптики, где волновой параметр Р<< 1. Из этого условия и определения (2) следует r<<d2 / λ;При заданных параметрах d2 / λ; = 800 м, т.е. дифракция незаметна в области ТЕМА 6. ОСЕСИММЕТРИЧНЫЕ ДИФРАКЦИОННЫЕ ЗАДАЧИ Решение многих физических задач значительно упрощается, если изучаемые системы обладают высокой степенью симметрии. Известными примерами служат расчеты моментов инерции и напряженности полей в случаях, когда распределение масс, зарядов или токов симметричны. Не являются исключением и дифракционные задачи. Среди них выделяют класс осесимметричных задач. В них между точечным источником волны S и точкой наблюдения Р находится препятствие, осью симметрии которого служит прямая SP. Пример - круглое отверстие в непрозрачном экране, на который нормально падает плоская или сферическая волна. Более важные примеры - различные оптические элементы, такие как объективы, диафрагмы, зеркала, входящие в реальные оптические устройства. Описание таких устройств - решение осесимметричных задач. Часто эти задачи решают, используя приближение зон Френеля и метод векторных диаграмм. Поскольку встречающиеся при этом результаты и выводы весьма поучительны, рассмотрим решения таких задач детально.
для центральной, средней и внешней подзон. При увеличении числа подзон число складываемых векторов возрастает, а их длины уменьшаются. Поэтому в пределе бесконечного числа подзон волны, идущие от первой зоны Френеля, изображаются гладким полувитком, начало которого в точке O соответствует нулевой фазе, а конец в точке K1, равной π;. Следовательно, результирующая волна в точке Р от первой зоны Френеля может быть изображена вектором OK1, при этом ее интенсивность равна
что интенсивность оптической оси SP под различными углами. Из-за этого интенсивности I1 и I2 не совпадают, незначительно отличаясь друг от друга, I1 -I2< <I1, (1) так что точка K2 не совпадает с точкой О. Поэтому диаграмма выглядит как виток спирали, а не как окружность.
Интенсивность в этом случае
Большинство осесимметричных дифракционных задач решается так: 1. Изображают векторную диаграмму для сво-
бодного пространства (спираль ОС), причем считают, что интенсивность 2. На спирали отмечают открытые зоны Френеля. 3. Подсчитывают длину результирующего вектора. 4. Квадрат модуля результирующего вектора дает искомую интенсивность IР дифрагировавшей волны в точке наблюдения. Для несимметричных систем такой метод решения малопригоден.
Оказывается, что появление данного непрозрачного экрана увеличивает интенсивность волны в точке наблюдения в 4 раза! ЗАДАЧА 2. В условиях предыдущей задачи экран открывает 1-ю и 2-ю зоны Френеля. Найти интенсивность IР. На приведенной выше векторной диаграмме следует оставить вклады от 1-й и 2-й зон,т.е. часть спирали ОК1K 2. Результирующим является вектор Следовательно, отверстия уменьшает интенсивность результирующей волны) объясняется тем, что равные по амплитуде волны от 1-й и 2-й зон приходят в точку наблюдения в противофазе и, интерферируя, гасят друг друга.
причем
зона, то результирующий вектор равен IР/I0=1 Наличие экрана не изменяет интенсивности волны. Но физически наличие или отсутствие экрана — различные ситуации. Что же изменяется при закрытии первой зоны Френеля в данном случае? Изменяется на п фаза результирующей волны в точке наблюдения.
Векторная диаграмма для работающих зон имеет вид
|


 в момент t. Уравнение (1) является простейшим. В него входит квадрат скорости звука
в момент t. Уравнение (1) является простейшим. В него входит квадрат скорости звука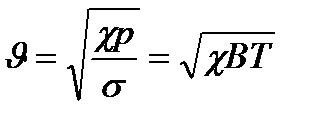 (2)
(2)
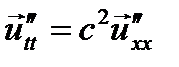 или
или  (4)
(4)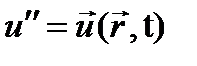 может принимать смысловые значения
может принимать смысловые значения  и
и  .
.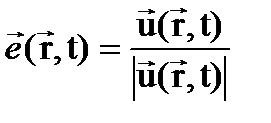
 может быть постоянным.
может быть постоянным.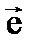 сонаправлен с направлением распространения волны, то говорят, что волна продольная (например, продольные смещения в упругом стержне). Если вектор
сонаправлен с направлением распространения волны, то говорят, что волна продольная (например, продольные смещения в упругом стержне). Если вектор  , у продольной волны
, у продольной волны  , тогда как у поперечной волны
, тогда как у поперечной волны 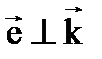 .
.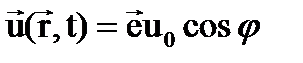 ,
, 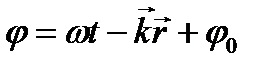 ,
,  .
. = 0, где
= 0, где  - единичный вектор, направленный вдоль оси у. Искомая волновая функция имеет при этом вид
- единичный вектор, направленный вдоль оси у. Искомая волновая функция имеет при этом вид ,
,  .
. .
.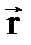 . Поэтому вектор поляризации в данном случае имеет вид
. Поэтому вектор поляризации в данном случае имеет вид  . Следовательно, общий вид волновой функции
. Следовательно, общий вид волновой функции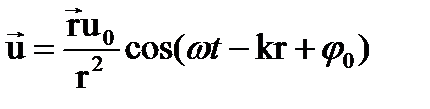

 ,
, 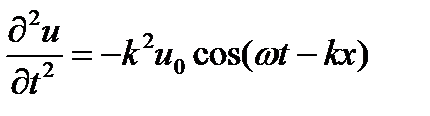 Подставляя (8) и (9) в (1) получим для любых х, t равенство –ω2 =v2(-k2), переходящее в тождество при учёте определения v = ω / k.Следовательно, заданная функция является решением уравнения (1).
Подставляя (8) и (9) в (1) получим для любых х, t равенство –ω2 =v2(-k2), переходящее в тождество при учёте определения v = ω / k.Следовательно, заданная функция является решением уравнения (1).
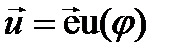 ,
,  есть решение уравнения (4),если
есть решение уравнения (4),если =const и постоянные числа b/a = ±v.
=const и постоянные числа b/a = ±v. из под знаков производных и умножим на
из под знаков производных и умножим на 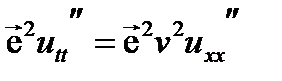 . (10)
. (10) и
и 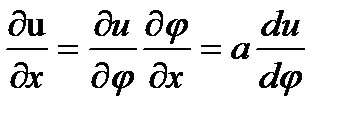
 (11)
(11)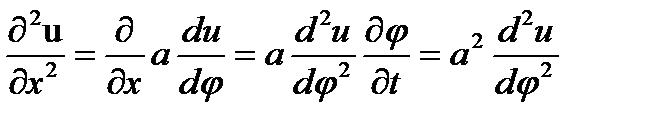 (12)
(12) (1)
(1) (4)
(4)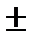 1. Стоячие волны легко возбудить на струне, концы которой закреплены неподвижно.
1. Стоячие волны легко возбудить на струне, концы которой закреплены неподвижно.
 , проведённый из начала координат в точку А,причём длина вектора равна амплитуде и0,а угол с полярной осью равен φ. Если волновая функция векторная, то длина вектора а равняется модулю |
, проведённый из начала координат в точку А,причём длина вектора равна амплитуде и0,а угол с полярной осью равен φ. Если волновая функция векторная, то длина вектора а равняется модулю |  0|.
0|.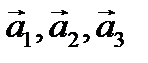 . Сложив их по правилу треугольников, получим результирующий вектор
. Сложив их по правилу треугольников, получим результирующий вектор  , длина которого ОВ равна амплитуде результирующей волны, а угол θРЕЗ, образованный с осью z, - фазе результирующей волны в данный момент времени и в данной точке.
, длина которого ОВ равна амплитуде результирующей волны, а угол θРЕЗ, образованный с осью z, - фазе результирующей волны в данный момент времени и в данной точке. (5) имеет два решения u1 и u2, т.е.
(5) имеет два решения u1 и u2, т.е. 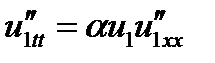 и
и 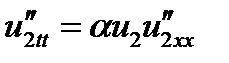 (6). Доказать, что для системы, описываемой уравнением (5), принцип суперпозиции не выполняется. Предположим обратное, т.е. считаем, что полная волновая функция и = и1+и2. (7) и найдём её производные. Тогда
(6). Доказать, что для системы, описываемой уравнением (5), принцип суперпозиции не выполняется. Предположим обратное, т.е. считаем, что полная волновая функция и = и1+и2. (7) и найдём её производные. Тогда  (8)
(8) (9)
(9)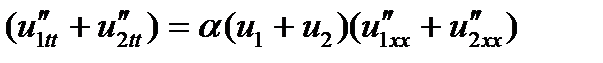
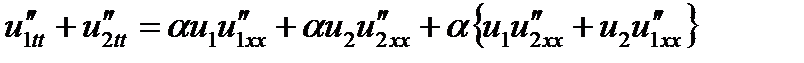 (10)
(10)
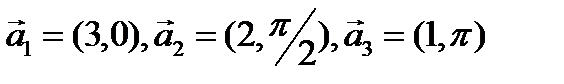 :
:
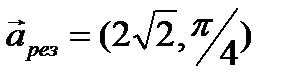 Поэтому результирующая волна имеет вид
Поэтому результирующая волна имеет вид 
 Значения их фаз см. в задаче 3.
Значения их фаз см. в задаче 3. РЕЗ| =
РЕЗ| =  , а фаза φРЕЗ = π/4. Волновая функция результирующей волны имеет вид
, а фаза φРЕЗ = π/4. Волновая функция результирующей волны имеет вид
 (1)
(1) - волновая функция, характеризующая возмущение данного физического параметра в момент времени t в точке
- волновая функция, характеризующая возмущение данного физического параметра в момент времени t в точке  , а
, а  - размерный
- размерный
 (2)
(2) (3)
(3) (4)
(4) суммарной волны отличается от суммы интенсивностей
суммарной волны отличается от суммы интенсивностей  и
и 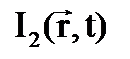 на величину перекрёстного или интерференционного слагаемого
на величину перекрёстного или интерференционного слагаемого 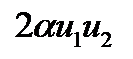 . Это слагаемое зависит от фаз волн u1 и u2. Поэтому говорят, что интерференция - это зависимость интенсивности результирующей волны от фаз складываемых волн. При сложении двух волн говорят о двулучевой интерференции. Если складывается большее число волн, то говорят о многолучевой интерференции. Такая интерференция важна в дифракционных явлениях.
. Это слагаемое зависит от фаз волн u1 и u2. Поэтому говорят, что интерференция - это зависимость интенсивности результирующей волны от фаз складываемых волн. При сложении двух волн говорят о двулучевой интерференции. Если складывается большее число волн, то говорят о многолучевой интерференции. Такая интерференция важна в дифракционных явлениях. (5)
(5) (6)
(6) и
и 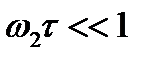 , то прибор позволяет следить за мгновенными значениями интерференции низкочастотных волн (пример - волны на поверхности воды).
, то прибор позволяет следить за мгновенными значениями интерференции низкочастотных волн (пример - волны на поверхности воды). и
и 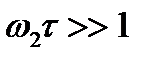 , то прибор не даёт возможности наблюдать
, то прибор не даёт возможности наблюдать (7)
(7) )
)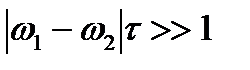 , то оба косинуса под интегралом в (7) при усреднении дают нулевые вклады и интерференционный член равен нулю. Эти волны недостаточно когерентны для наблюдения их интерференции данным прибором.
, то оба косинуса под интегралом в (7) при усреднении дают нулевые вклады и интерференционный член равен нулю. Эти волны недостаточно когерентны для наблюдения их интерференции данным прибором.
 (10)
(10) . Интенсивность суммарной волны
. Интенсивность суммарной волны  , где
, где 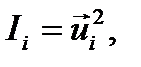
 ,
, (11)
(11)
 (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)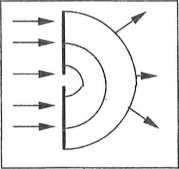 Например, если плоская волна падает на экран со щелью, то фиктивные источники, расположенные на поверхности, совпадающей с плоскостью щели, создают вторичные сферические волны, распространяющиеся за экраном, причём их огибающая заходит за непрозрачную часть экрана. Возникает явление, называемое дифракцией. Как и интерференция, дифракция - обязательный признак волновых процессов. Основываясь на принципе Гюйгенса дают “узкое” определение дифракции.
Например, если плоская волна падает на экран со щелью, то фиктивные источники, расположенные на поверхности, совпадающей с плоскостью щели, создают вторичные сферические волны, распространяющиеся за экраном, причём их огибающая заходит за непрозрачную часть экрана. Возникает явление, называемое дифракцией. Как и интерференция, дифракция - обязательный признак волновых процессов. Основываясь на принципе Гюйгенса дают “узкое” определение дифракции. . Плотность фиктивных источников одинакова, а площади колец примерно равны, поэтому амплитуды волн, идущих от колец, равны, а их фазы отличаются на π. В результате волны от соседних колец приходят в P в противофазе и их суммарная интенсивность равна нулю благодаря интерференции. 3. Отмечать “открытые” и “закрытые” препятствиями зоны, что позволяет находить интенсивность результирующей волны в точке наблюдения.
. Плотность фиктивных источников одинакова, а площади колец примерно равны, поэтому амплитуды волн, идущих от колец, равны, а их фазы отличаются на π. В результате волны от соседних колец приходят в P в противофазе и их суммарная интенсивность равна нулю благодаря интерференции. 3. Отмечать “открытые” и “закрытые” препятствиями зоны, что позволяет находить интенсивность результирующей волны в точке наблюдения.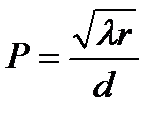 (2)
(2)

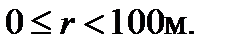 Верхняя граница условна.
Верхняя граница условна. Рассмотрим вспомогательную сферическую поверхность F выделим на ней первую зону Френеля. По определению - это симметричная область AA’, такая, что ар -ОР= λ/2. В результате такого выбора волны от центральной области вокруг точки О и от окружности AA’ различаются по фазе на π;.
Рассмотрим вспомогательную сферическую поверхность F выделим на ней первую зону Френеля. По определению - это симметричная область AA’, такая, что ар -ОР= λ/2. В результате такого выбора волны от центральной области вокруг точки О и от окружности AA’ различаются по фазе на π;. и
и 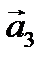
 .
.
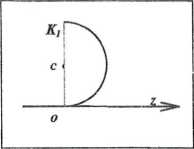 Вторая зона Френеля может быть рассмотрена подобным образом. Поскольку ее площадь равна площади первой зоны, то
Вторая зона Френеля может быть рассмотрена подобным образом. Поскольку ее площадь равна площади первой зоны, то  На векторной диаграмме волна, идущая от второй зоны в точку наблюдения Р, изобразится полувитком К1, K2, так
На векторной диаграмме волна, идущая от второй зоны в точку наблюдения Р, изобразится полувитком К1, K2, так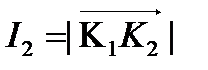 . Зоны наклонены к
. Зоны наклонены к Если рассматривать остальные зоны Френеля, то векторная диаграмма примет вид бесконечной спирали с фокусом в точке с. Справа от ОК, лежат части спирали, соответствующие нечетным зонам Френеля, слева - соответствующие четным зонам. Результирующий вектор, проведенный из начала спирали O в ее конец с, определяет полную интенсивность IР волны в точке наблюдения Р при отсутствии препятствий, т.е. в свободном пространстве, когда открыты все зоны Френеля.
Если рассматривать остальные зоны Френеля, то векторная диаграмма примет вид бесконечной спирали с фокусом в точке с. Справа от ОК, лежат части спирали, соответствующие нечетным зонам Френеля, слева - соответствующие четным зонам. Результирующий вектор, проведенный из начала спирали O в ее конец с, определяет полную интенсивность IР волны в точке наблюдения Р при отсутствии препятствий, т.е. в свободном пространстве, когда открыты все зоны Френеля.
 Указывая, какие зоны Френеля открыты или же работают, можно с помощью векторной диаграммы определить интенсивность результирующей волны в точке наблюдения.
Указывая, какие зоны Френеля открыты или же работают, можно с помощью векторной диаграммы определить интенсивность результирующей волны в точке наблюдения.
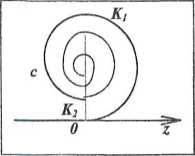 ЗАДАЧА 1. Имеется непрозрачный экран, в котором для данной длины волны λ и данной точки наблюдения открыта первая зона Френеля. Найти интенсивность IР, если I0 считается заданной. Построив спираль, соответствующую свободному пространству, отметим на ней вклад первой зоны Френеля, т.е. вектор
ЗАДАЧА 1. Имеется непрозрачный экран, в котором для данной длины волны λ и данной точки наблюдения открыта первая зона Френеля. Найти интенсивность IР, если I0 считается заданной. Построив спираль, соответствующую свободному пространству, отметим на ней вклад первой зоны Френеля, т.е. вектор  Остальные зоны закрыты и вторичные волны от них не идут. От спирали надо оставить только полувиток ОК1. Тогда результирующий вектор равен
Остальные зоны закрыты и вторичные волны от них не идут. От спирали надо оставить только полувиток ОК1. Тогда результирующий вектор равен  . Следовательно, интенсивность в точке наблюдения
. Следовательно, интенсивность в точке наблюдения
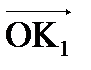 . Но в силу (1) шаг спирали весьма мал и
. Но в силу (1) шаг спирали весьма мал и  .
. . Парадоксальность результата (увеличение размера
. Парадоксальность результата (увеличение размера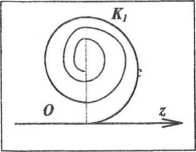 ЗАДАЧА 3. Непрозрачный экран представляет собой круг, закрывающий 1-ю зону Френеля. Найти отношение интенсивности волн IР/I0.Векторная диаграмма для волны в свободном пространстве имеет вид спирали OC,
ЗАДАЧА 3. Непрозрачный экран представляет собой круг, закрывающий 1-ю зону Френеля. Найти отношение интенсивности волн IР/I0.Векторная диаграмма для волны в свободном пространстве имеет вид спирали OC,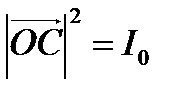 . Так как закрыта только первая
. Так как закрыта только первая . Значит
. Значит 
 ЗАДАЧА 4. Под зонной пластинкой подразумевается непрозрачная кольцевая структура, закрывающая часть четных (или нечетных) зон Френеля. Найти интенсивность результирующей волны, если зонная пластинка закрывает п четных зон Френеля.
ЗАДАЧА 4. Под зонной пластинкой подразумевается непрозрачная кольцевая структура, закрывающая часть четных (или нечетных) зон Френеля. Найти интенсивность результирующей волны, если зонная пластинка закрывает п четных зон Френеля.


