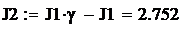Лабораторная работа №1. Российская Таможенная Академия

Российская Таможенная Академия

(название таможенного, правоохранительного органа)

 

19.03.2012 – 31.03.2012

(начало и окончание практики)

 

 

Студент 2 курса Бочкарева М.С.

(подпись) (Ф.И.О.)

 

Руководитель практики

от таможенного

(правоохранительного) органа

(подпись) (Ф.И.О.)

 

Руководитель практики от Мозжегорова О.А.

Академии

(подпись) (Ф.И.О.)

 

 

Люберцы

 

Лабораторная работа №1

"Идентификация параметров двухмассовой модели

механической части электропривода "

 

Цель работы: изучение влияния параметров двухмассовой механической части электропривода с упругим звеном на ее свойства как объекта управления с помощью частотных характеристик.

 

Ход работы:

 

 

1) Частотные характеристики структурной схемы и значения частот в точках резонанса

Ответы на контрольные вопросы:

1) При каких условиях можно пренебрегать влиянием упругости и рассматривать механическую часть привода как жесткое звено?

 

При составлении кинематической схемы принято, что механическая часть привода содержит n вращательно движущихся сосредоточенных масс и k поступательно, причем механическая инерция элементов, связывающих эти массы, не учитывается. Каждый вращательно движущийся элемент обладает моментом инерции J, и связан с (i + 1)-м элементом механической связью, обладающей жесткостью с_i Соответственно каждый поступательно движущийся элемент имеет массу т_j и связан со следующим механической связью с жесткостью с_j. Массы элементов и жесткости элементарных связей в кинематической цепи привода различны. Определяющее влияние на движение системы оказывают наибольшие массы и наименьшие жесткости связей.

Для составления расчетных схем механической части электропривода необходимо приведение всех параметров элементов кинематической цепи к одной расчетной скорости. Обычно наибольшее удобство представляет приведение их к скорости двигателя. Условием соответствия приведенной расчетной схемы реальной механической системе является выполнение закона сохранения энергии. При приведении необходимо обеспечить сохранение запаса кинетической и потенциальной энергии системы, а также элементарной работы всех действующих в системе сил и моментов на возможных перемещениях. Откуда получаем формулы приведения

где i_1i=w₁/w_i - передаточное число от вала приведения до i-го вала; p_1j=v_i/w₁ - радиус приведения к валу со скоростью w₁.

Когда параметры системы таковы, что влияние упругих связей незначительно, или при решении задач, в которых с этим влиянием можно не считаться, механическая часть представляется простейшей расчетной схемой, не учитывающей влияния упругих связей, - жестким приведенным звеном. В этих случаях многомассовая механическая часть электропривода заменяется одной эквивалентной массой с моментом инерции J_S, на которую воздействуют электромагнитный момент двигателя М и суммарный приведенный к валу двигателя момент нагрузки M_с. Момент нагрузки М_с включает в себя все внешние силы, приложенные к механической системе, кроме момента двигателя M.

Если при синтезе электропривода используются обратные связи только по переменным двигателя, то при J2<<J1 или W12>>Wc где Wс - частота среза желаемой ЛАЧХ разомкнутого контура регулирования, механическую часть электропривода можно представить жестким механическим звеном, не учитывая влияния упругостей.

 

 

2) Почему происходит затухание колебаний в реальной двухмассовой системе и в чем это проявляет себя на частотных характеристиках?

 

В реальных системах присутствуют диссипативные силы, которые оказывают на колебательную систему демпфирующее действие. Это демпфирование в большинстве случаев невелико. Естественное затухание колебаний под действием внутренних сил вязкого трения можно характеризовать значениями логарифмического декремента

где a_вт и W_p=W₁₂ - коэффициент затухания и резонансная частота колебаний с учетом влияния внутренних диссипативных сил.

 

Рисунок 1.4 Логарифмические частотные характеристики двухмассовой упругой

системы по управляющему воздействию:

а – при выходной переменной ω₁; б - при выходной переменной ω₂.

Учет естественного демпфирования существенно не сказывается на форме ЛАЧХ и ЛФЧХ системы, однако, ограничивает резонансный пик конечными значениями, как показано штриховой кривой 1 на рисунок 1.4, а, и несколько сглаживает фазочастотную характеристику (штриховая кривая 2 на том же рисунке). Аналогичные изменения, вносимые естественным демпфированием в частотные характеристики на рисунок 1.4, б, показаны штриховыми кривыми, обозначенными соответственно 1' и 2'.

 

3) При каких условиях поведение первой и второй масс в упругой системе одинаковое?

 

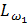В низкочастотной области асимптоты ЛАЧХ и 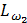совпадают, т.к. в среднем движение второй массы, как и первой, определяется действием интегрирующего звена , разрыв имеет место только на резонансной частоте Ω₁₂.

 

 

	рад/с		рад/с

4) Исходя из решения характеристического уравнения определим коэффициент жесткости с12 двухмассовой системы

 

Передаточная функция W1(p)/M(p)

2) Определим коэффициент соотношения масс

3) Определим момент инерции второй массы, задаваясь значением момента инерции первой

м·с2

откуда

	м·с2