Таким образом, тепловой эффект реакции равен –853,8 кДж, а составляет –822,2 кДж/моль.
Пример 3.3. Исходя из термохимических уравнений: Н2 (г) + О2 (г) = Н2О2 (ж), Δ Н° (1) = –187 кДж; (1) Н2О2 (ж) + Н2 (г) = 2Н2О (г), Δ Н° (2) = –297 кДж; (2) Н2О (г) = Н2О (ж), Δ Н° (3) = – 44 кДж, (3) рассчитать значение стандартной энтальпии реакции образования Н2О (ж). Решение. Запишем уравнение реакции, тепловой эффект которой необходимо определить: Н2 (г) + ½О2 (г) = Н2О (ж), Δ Н° (4) –?(4) В уравнения (1), (2), (3) входят Н2О2 (ж) и Н2О (г), которые не входят в уравнение (4). Чтобы исключить их из уравнений (1), (2), (3), умножим уравнение (3) на 2 и сложим все три уравнения: Н2 (г) + О2 (г) + Н2О2 (ж) + Н2 (г) + 2Н2О (г) = Н2О2 (ж) + 2Н2О (г) + 2Н2О (ж). (5) После преобразования уравнения (5) и деления его на 2 получаем искомое уравнение (4). Аналогичные действия проделаем с тепловыми эффектами:
В результате получаем т. е. энтальпия образования Н2О (ж): Пример 3.4. В каком направлении будет протекать при стандартных условиях реакция СН4 (г) + СО2 (г) ↔ 2СО (г) + 2Н2 (г)? Решение. Направление протекания химической реакции определяет энергия Гиббса (∆ G). Изменение энергии Гиббса в результате химической реакции равно сумме энергий Гиббса образования продуктов реакции за вычетом суммы энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов. Формула для расчета изменение энергии Гиббса изучаемой реакции имеет вид
Значения Δ f G° берем из табл. Б. 1 и получаем Δ f G° = [2∙(–137,1) + 2∙0] − [(–50,8) + (–394,4)] = +171 кДж. При р = const, T = const реакция самопроизвольно протекает в том направлении, которому отвечает убыль энергии Гиббса. Если ∆ G < 0, то реакциясамопроизвольно протекает в прямом направлении. Если ∆ G > 0, то самопроизвольное протекание процесса в прямом направлении невозможно. Если ∆ G = 0, то реакция может протекать как в прямом направлении, так и в обратном, и система находится в состоянии равновесия. Так как ∆ G° х.р. = +171 кДж, т.е. ∆ G > 0, то самопроизвольное протекание данной реакции в прямом направлении в стандартных условиях невозможно. Пример 3.5. Определить изменение энтропии в стандартных условиях для реакции, протекающей по уравнению С (графит) + 2Н2 (г) = СН4 (г). Решение. Изменение энтропии системы в результате протекания химической реакции (∆ S) (энтропия реакции) равно сумме энтропий продуктов реакции за вычетом суммы энтропий исходных веществ с учетом стехиометрических коэффициентов:
Подставляем в формулу справочные данные из табл. Б. 1 и получаем: ∆ S° х.р. = 186,2 − (5,7 + 2∙130,6) = –80,7 Дж/К. Пример 3.6. По значениям стандартных энтальпий образования и стандартных энтропий веществ, участвующих в реакции, вычислить изменение энергии Гиббса реакции, протекающей по уравнению СО (г) + Н2О (ж) = СО2 (г) + Н2 (г). Решение. Изменение энергии Гиббса в химической реакции при температуре Т можно вычислить по уравнению ∆ G° х.р. = ∆ Н° х.р. – Т ∆ S° х.р.. Тепловой эффект реакции ∆ Н° х.р. и изменение энтропии ∆ S° х.р. определяем по следствию из закона Гесса:
Используя справочные данные табл. Б. 1, получаем: ∆ Н° х.р. = [(–393,5) + 0] − [(–110,5) + (–285,8)] = +2,8 кДж; ∆ S° х.р. = (213,7 + 130,6) − (197,5 + 70,1) = +76,7 Дж/К. Изменение энергии Гиббса в химической реакции: ∆ G° х.р. = ∆ Н° х.р. – Т ∆ S° х.р.; Т = 298 К; ∆ G° х.р. = 2,8 − 298∙76,7∙10-3 = –20,05 кДж. Пример 3.7. Определить температуру, при которой установится равновесие в системе СаСО3 (к) Решение. При химическом взаимодействии одновременно изменяется энтальпия, характеризующая стремление системы к порядку, и энтропия, характеризующая стремление системы к беспорядку. Если тенденции к порядку и беспорядку в системе одинаковы, то ∆ H° х.р. = Т ∆ S° х.р., что является условием равновесного состояния системы. Отсюда можно определить температуру, при которой устанавливается равновесие химической реакции для стандартного состояния реагентов:
Сначала вычисляем ∆ Н° х.р. и ∆ S° х.р.по формулам:
Используя справочные данные табл. Б. 1 получаем: D H °х.р.= [– 635,5 + (–393,5)] – (–1207,1) = 178,1 кДж; D S °х.р. = (39,7 + 213,7) – 92,9 = 160,5 Дж/К или 0,1605 кДж/К. Отсюда температура, при которой устанавливается равновесие: Т равн. = 178,1/0,1605 = 1109,5 К. Пример 3.8. ВычислитьD H° х.р., ∆ S° х.р. и D G°T реакции, протекающей по уравнению Fe2O3 (к) + 3C (к) = 2Fe (к) + 3CO (г). Возможна ли реакция восстановления Fe2O3 углеродом при температуре 298 и 1000 К? Решение. Вычисляем D H° х.р. и D S° х.р.:
D H°х.р. =[3(–110,5) + 2·0] – [–822,2 + 3·0] = –331,5 + 822,2 = +490,7 кДж;
D S° х.р. = (2·27,2 + 3·197,5) – (89,9 + 3·5,7) = 539,9 Дж/К или 0,540 кДж/К. Энергию Гиббса при соответствующих температурах находим из соотношения D G° х.р. = D H°х.р. – Т D S°х.р.. D G° 298 = 490,7 – 298×0,540 = +329,8 кДж; D G° 1000 = 490,7 – 1000×0,540 = –49,3 кДж. Так как D G° 298 > 0, а D G° 1000< 0, то восстановление Fe2O3 углеродом возможно при 1000 К и невозможно при 298 К.
|

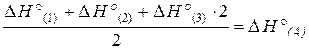 .
.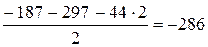 кДж,
кДж,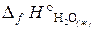 = –286 кДж/моль.
= –286 кДж/моль.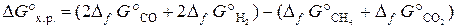 .
.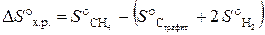 .
. ;
; .
. СаО (к) + СО2 (г).
СаО (к) + СО2 (г). .
.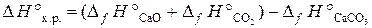 ;
;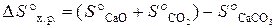 .
. ,
, ,
,


