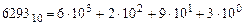ЛАБОРАТОРНАЯ РАБОТА 1. Системы счисления
На практике при анализе устойчивости систем с заданным характеристическим уравнением часто пользуются алгоритмом Рауса. Это алгоритм, как и алгоритм Гурвица, основывается на анализе специальной таблицы – таблицы Рауса (матрицы Рауса)
Она составляется из коэффициентов характеристического уравнения системы с помощью следующих правил: в первой строке располагаются коэффициенты характеристического уравнения с четными индексами (0, 2, 4,...), во второй – с нечетными (1, 3, 5,..._. Элементы
Здесь Эти формулы и определяют по существу алгоритм Рауса. Проверка устойчивости системы осуществляется в ходе заполнения таблицы Рауса. В соответствии с критерием Рауса для устойчивости системы необходимо и достаточно, чтобы (при a0 >0) выполнялось неравенство di >0 (i =3,..., n +2) или (что эквивалентно) a0 >0, a1 >0,
ЛАБОРАТОРНАЯ РАБОТА 1. Системы счисления Система счисления, или просто счисление, или нумерация,— набор конкретных знаков–цифр вместе с системой приемов записи, которая представляет числа этими цифрами. Цель работы – приобретение навыков выполнения операций в различных системах счисления.
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: Различают два типа систем счисления: - позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа; - непозиционные, когда значение цифры в числе не зависит от ее места в записи числа. Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно. Любое целое число в позиционной системе можно записать в форме многочлена:
где
n — количество разрядов числа. Пример. Число
Десятичная система счисления – в настоящее время наиболее известная и используемая. неправильное название удерживается и поныне. Десятичная система использует десять цифр —– 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа. В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Таблица 1. Соответствие чисел, записанных в различных системах счисления
|


 (i>=3) в остальных строках вычисляются с помощью рекуррентных соотношений:
(i>=3) в остальных строках вычисляются с помощью рекуррентных соотношений:
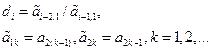
 Если какой-нибудь из перечисленных коэффициентов отрицателен, то система неустойчива. Более того, число перемен знаков у коэффициентов первого столбца таблицы Рауса дает нам число корней характеристического уравнения системы, которые расположены в правой полуплоскости.
Если какой-нибудь из перечисленных коэффициентов отрицателен, то система неустойчива. Более того, число перемен знаков у коэффициентов первого столбца таблицы Рауса дает нам число корней характеристического уравнения системы, которые расположены в правой полуплоскости.

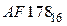 .
. ,
,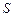 — основание системы счисления;
— основание системы счисления; — цифры числа, записанного в данной системе счисления;
— цифры числа, записанного в данной системе счисления; запишется в форме многочлена следующим образом:
запишется в форме многочлена следующим образом: