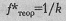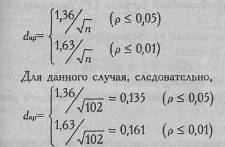Пример 1: Сопоставление эмпирического распределения с теоретическим

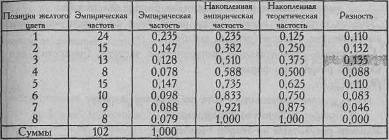
Ввыборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний воз­раст 20 лет, проводился тест Люшера в 8-цветном варианте. Установ­лено, что желтый цвет предпочитается испытуемыми чаще, чем отверга­ется (Табл. 4.16). Можно ли утверждать, что распределение желтого цвета по 8-и позициям у здоровых испытуемых отличается от равно­мерного распределения?

Таблица 4.16

Эмпирические частоты попадания желтого цвета на каждую из 8 позиций (n =102)

Сформулируем гипотезы.

H₀: Эмпирическое распределение желтого цвета по восьми позициям не отличается от равномерного распределения.

H₁: Эмпирическое распределение желтого цвета по восьми позициям отличается от равномерного распределения.

Теперь приступим к расчетам, постепенно заполняя результатами таблицу расчета критерия λ. Все операции лучше прослеживать по Табл. 4.17, тогда они будут более понятными.

Занесем в таблицу наименования (номера) разрядов и соответст­вующие им эмпирические частоты (первый столбец Табл. 4.17). Затем рассчитаем эмпирические частости f * по формуле:

f*_j = f_j /n

где f_j - частота попадания желтого цвета на данную позицию;

n - общее количество наблюдений; j - номер позиции по порядку.

Запишем результаты во второй столбец (см. Табл. 4.17). Теперь нам нужно подсчитать накопленные эмпирические часто­сти Σ f *. Для этого будем суммировать эмпирические частости f *. На­пример, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда, Σ f *₁=0,235[20].

Для 2-го разряда накопленная эмпирическая частость будет пред­ставлять собой сумму эмпирических частостей 1-го и 2-го разрядов:

Σ f *₁₊₂=0,235+0,147=0,382

Для 3-го разряда накопленная эмпирическая частость будет пред­ставлять собой сумму эмпирических частостей 1-го, 2-го и 3-го разрядов:

Σ f*_{1 +2+3}=0,235+0,147+0,128=0,510

Мы видим, что можно упростить задачу, суммируя накопленную эмпирическую частость предыдущего разряда эмпирической частостью данного разряда, например, для 4-го разряда:

Σ f *_1+2+3+4=0,510+0,078=0,588

Запишем результаты этой работы в третий столбец.

Теперь нам необходимо сопоставить накопленные эмпирические частости с накопленными теоретическими частостями. Для 1-го разряда теоретическая частость определяется по формуле:

где k - количество разрядов (в данном случае - позиций цвета).

Для рассматриваемого примера:

f *_теор=1/8=0,125

Эта теоретическая частость относится ко всем 8-и разрядам. Действительно, вероятность попадания желтого (или любого другого) цвета на каждую из 8-и позиций при случайном выборе составляет 1/8, т.е. 0,125.

Накопленные теоретические частости для каждого разряда опре­деляем суммированием. Для 1-го разряда накопленная теоретическая частость равна теоретической частости попадания в разряд:

f * _{т 1}=0,125

Для 2-го разряда накопленная теоретическая частость представ­ляет собой сумму теоретических частостей 1-го и 2-го разрядов: f *_{т 1+2}=0,125+0,125=0,250

Для 3-го разряда накопленная теоретическая частость представ­
ляет собой сумму накопленной к предыдущему разряду теоретической
частости с теоретической частостью данного разряда:

f *_{т 1+2+3}=0,250+0,125=0,375

Можно определить теоретические накопленные частости и путем!
умножения:

S f * _{т j}= f * _{теор j}

где f *_теор - теоретическая частость; j - порядковый номер разряда.

Занесем рассчитанные накопленные теоретические частости в четвертый столбец таблицы (Табл. 4.17).

Теперь нам осталось вычислить разности между эмпирическими и теоретическими накопленными частостями (столбцы 3-й и 4-й). В пя­тый столбец записываются абсолютные величины этих разностей, обо­значаемые как d.

Определим по столбцу 5, какая из абсолютных величин разности является наибольшей. Она будет называться d_max. В данном случае d_max=0,135.

Теперь нам нужно обратиться к Табл. X Приложения 1 для оп­ределения критических значений d_max при n =102.

Таблица 4.17

Расчет критерия при сопоставлении распределения выборов желтого цвета с равномерным распределением (n =102)

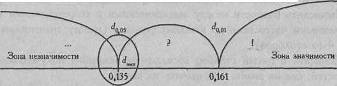
Очевидно, что чем больше различаются распределения, тем больше и различия в накопленных частостях. Поэтому нам не составит труда распределить зоны значимости и незначимости по соответствую­щей оси:

Очевидно, что чем больше различаются распределения, тем больше и различия в накопленных частостях. Поэтому нам не составит труда распределить зоны значимости и незначимости по соответствую­щей оси:

d_эмп=0,135

d_эмп=dкр.

Ответ: Н₀ отвергается при р=0,05. Распределение желтого цве­та по восьми позициям отличается от равномерного распределения. Представим все выполненные действия в виде алгоритма