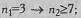Гипотезы
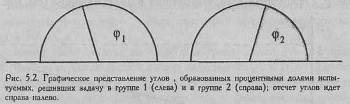
H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2. H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2. Графическое представление критерия φ* Метод углового преобразования несколько более абстрактен, чем остальные критерии. Формула, которой придерживается Е. В. Гублер при подсчете значений φ, предполагает, что 100% составляют угол φ=3,142, то есть округленную величину π=3,14159... Это позволяет нам представить сопоставляемые выборки в виде двух полукругов, каждый из которых символизирует 100% численности своей выборки. Процентные доли испытуемых с "эффектом" будут представлены как секторы, образованные центральными углами φ. На Рис. 5.2 представлены два полукруга, иллюстрирующие Пример 1. В первой выборке 60% испытуемых решили задачу. Этой процентной доле соответствует угол φ=1,772. Во второй выборке 40% испытуемых решили задачу. Этой процентной доле соответствует угол φ =1,369.
Критерий φ* позволяет определить, действительно ли один из углов статистически достоверно превосходит другой при данных объемах выборок. Ограничения критерия φ* 1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным (Гублер Е.В., 1978, с. 86). 2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими. Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок: а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:
б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:
в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:
г) при n1,n2≥5 возможны любые сопоставления. В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n1 =2, n2 =15, но в этих случаях не удастся выявить достоверных различий. Других ограничений у критерия φ* нет. Рассмотрим несколько примеров, иллюстрирующих возможности критерия φ*. Пример 1: сопоставление выборок по качественно определяемому признаку. Пример 2: сопоставление выборок по количественно измеряемому признаку. Пример 3: сопоставление выборок и по уровню, и по распределению признака. Пример 4: использование критерия φ* в сочетании с критерием X Колмогорова-Смирнова в целях достижения максимально точного результата.
|