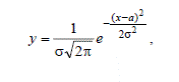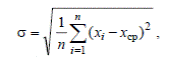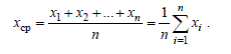ОЦЕНКИ ПОГРЕШНОСТЕЙ

1.6.1. ЗАКОН НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Указанный метод используется для установления наиболее вероятного значения размеров обрабатываемой заготовки при данных условиях обработки. Метод основан на проведении обработки опытной партии заготовок с замерами требуемого параметра (размера). В полученном ряде размеров l i выявляются предельные значения и определяется размах распределения Δ P.

Значения Δ P разбивают на равные интервалы и определяют частность повторений ω отклонения размеров в каждом интервале

где m – число заготовок, фактический размер которых находится в переделах данного интервала; n – общее число деталей в партии.

 

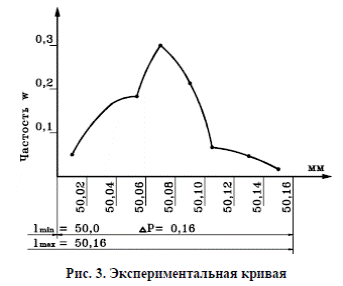
Далее строят график (полигон) распределения размеров (рис. 3).

П р и м е р: n = 100 шт., Δ P = 0,16 мм, интервал – 0,02 мм.

I – размерная группа – 5 дет. ω = 0,05

II – размерная группа – 13 дет. ω = 13 и т.д.

Известно, что распределение суммы большого числа взаимно независимых случайных слагаемых величин с малым влиянием каждой на общую сумму при отсутствии доминирующих факторов подчиняется закону нормального распределения.

Для повышения плавности ломанной линии увеличивают число деталей (n) и уменьшают интервал (например, принимают 0,01 мм).

Установлено, что при обработке заготовок способом автоматического получения размеров точность обработки подчиняется закону нормального распределения (рис. 4), который изображается математической кривой Гаусса с уравнением:

где σ – среднеквадратичное отклонение аргумента; l – основание натурального логарифма; a – центр группирования значений аргумента и в то же время среднеарифметическое отклонение аргумента.

Среднеквадратичное отклонение:

где n – число измерений; xi – текущее значение измерения; x ср – среднее арифметическое данных измерений.

Число n необходимо брать 50 и более.

Кривая нормального распределения симметрична. Ордината вершины Y max будет при x = a

Точка перегиба находится на расстоянии:

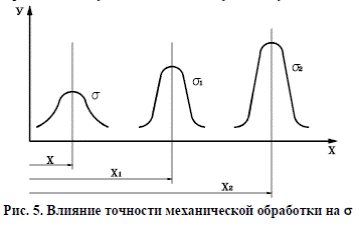
Величина σ характеризует форму кривой распределения и является

мерой точности данного метода обработки. С увеличением точности обработки σ уменьшается.

На рисунке 5 показаны кривые распределения: σ – после предварительного точения; σ1 – после чистового точения; σ2 – после шлифования.

При правильном построении технологического маршрута обработки σ > σ1 > σ2.

Изучение кривых распределения погрешностей позволяет выявить соотношения между числом годных и бракованных изделий.

Если на обработку установлен допуск δ, который определяется величинами x 1 и x 2 от центра группирования, то заштрихованный участок соответствует числу заготовок, входящих в поле допуска.

Для определения площади (заштрихованной) необходимо проинтегрировать функцию y в пределах граничных значений x 1 и x 2.

Установлено, что в интервале x = ±3σ площадь, ограниченная этим участком, составляет 0,9973 всей площади, т.е. 99,73 % обработанных заготовок будут годными. Процент брака – 0,27. Таким образом точность любого способа обработки можно установить по величине 6σ (правило шести σ), что достаточно точно для практических расчетов (рис. 6).

Закону Гаусса подчиняются многие непрерывные случайные величины: размеры детали; вес заготовок и деталей машин; твёрдость и другие характеристики механических свойств; высота микронеровностей на обработанных поверхностях; погрешности измерения и другие величины.

Метод оценки точности на основе кривых распределения универсален, позволяет объективно оценить точность механической обработки и других механических операций, но не позволяет оценить изменения параметра во времени, нельзя отличить переменные систематические погрешности от случайных – и, как результат, – отсутствует возможность активного воздействия на технологический процесс обработки заготовки.