ПОТЕНЦИАЛ ДЕЙСТВИЯ
Еще Э. Бернштейн изучал процесс возбуждения клеточной мембраны и предсказал измерение ее проницаемости для различных ионов. Однако завершить изучение этого вопроса он не успел. Примерно в 1939 г. Коул и Кертис (США) и Ходжкин и Хаксли (Великобритания) измеряли потенциалы невозбужденной и возбужденной клеток на гигантском аксоне кальмара: оказалось, что в состоянии покоя разность потенциалов была примерно равна -80 мВ (отрицательная), а максимальная разность потенциалов при возбуждении +40мВ (положительная). Далее Ходжкин и Хаксли сформулировали гипотезу о том, что при возбуждении меняется характер проницаемости мембраны для разного типа ионов: из проницаемой главным образом для калия она превращается в проницаемую для натрия и, следовательно, поток ионов натрия внутрь клетки увеличивается. Разность потенциалов между поверхностями мембраны поднимается до нуля, а затем становится положительной – наступает деполяризация мембраны. Далее процесс развивается в обратном направлении: поток ионов натрия внутрь клетки постепенно уменьшается и возвращается к «невозбужденному» значению; разность потенциалов также возвращается к значению Ходжкин и Хаксли построили также электрическую модель процесса возбуждения, согласно этой модели мембрана представляется следующей схемой (рис. 4). На рис.4. изображены конденсатор емкости С, два переменных резистора, которым соответствуют проводимости Согласно этой модели полный ток, протекающий через мембрану, равен сумме 4 слагаемых: где Iк – ток ионов калия; INa –ток ионов натрия; I’ – ток ионов хлора и остальных ионов, иногда называемый током утечки; Рассмотрим сначала ток калия. Ионы калия идут через мембрану всегда, причем в обе стороны. Когда потенциал на мембране ( Аналогичной формулой определяется и сила натриевого тока:
Где Зависимости проводимостей gк и gNa от времени при некотором неизменном мембранном потенциале изучали в опытах Ходжкина – Хаксли (опыты с фиксацией напряжения). За очень короткое время на мембране устанавливали фиксированную разность потенциалов и долго поддерживали ее. Это позволяло, в частности, избавиться от емкостных токов: если
Рис. 5. позволяет, во-первых, сделать важный вывод о том, что проводимость gNa зависит от времени – ведь при постоянной разности потенциалов ток
|

 . Такой импульс (рис..3) называют потенциалом действия.
. Такой импульс (рис..3) называют потенциалом действия. , 3 источника ЭДС, имитирующих равновесные, рассчитанные по формуле Нернста разности потенциалов для ионов калия, натрия и хлора, а также еще одно сопротивление (суммарное сопротивление мембраны для ионов хлора и ряда других) – соответствующая проводимость обозначена на схеме.
, 3 источника ЭДС, имитирующих равновесные, рассчитанные по формуле Нернста разности потенциалов для ионов калия, натрия и хлора, а также еще одно сопротивление (суммарное сопротивление мембраны для ионов хлора и ряда других) – соответствующая проводимость обозначена на схеме.
 - емкостный ток (ток перезарядки мембраны), протекающий по той ветви цепи, куда включен конденсатор.
- емкостный ток (ток перезарядки мембраны), протекающий по той ветви цепи, куда включен конденсатор. ) равен нернстовскому потенциалу, который иначе называют потенциалом равновесия для калия
) равен нернстовскому потенциалу, который иначе называют потенциалом равновесия для калия  , то сохраняется динамическое равновесие, т.е. калиевый ток
, то сохраняется динамическое равновесие, т.е. калиевый ток  равен нулю. Если мембранный потенциал отклоняется от равновесного, то возникает калиевый ток, величину которого можно определить по закону Ома:
равен нулю. Если мембранный потенциал отклоняется от равновесного, то возникает калиевый ток, величину которого можно определить по закону Ома: 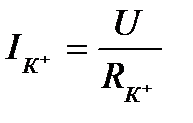 . Заменив
. Заменив  на калиевую проводимость
на калиевую проводимость  - на величину отклонения мембранного потенциала от равновесного, т.е.
- на величину отклонения мембранного потенциала от равновесного, т.е.  , получаем:
, получаем: 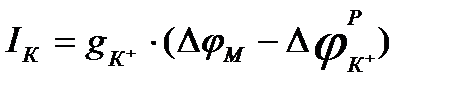
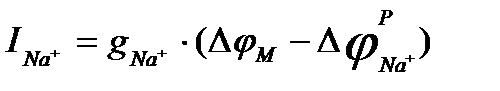 ,
, - равновесный натриевый потенциал, т.е. нернстовский потенциал для натрия, который равен примерно +40 мВ (он примерно равен овершуту – превышению нуля значением
- равновесный натриевый потенциал, т.е. нернстовский потенциал для натрия, который равен примерно +40 мВ (он примерно равен овершуту – превышению нуля значением 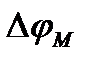 в точке максимума; Как видно, силы токов зависят от мембранного потенциала довольно сложным образом:
в точке максимума; Как видно, силы токов зависят от мембранного потенциала довольно сложным образом:  . Чтобы отдельно зарегистрировать токи ионов калия и натрия, использовали блокаторы. При введении тетраэтиламмония (блокатор калия) фиксировали зависимость тока ионов натрия от времени, при введении тетродотоксина – зависимость тока ионов калия от времени. Зависимость
. Чтобы отдельно зарегистрировать токи ионов калия и натрия, использовали блокаторы. При введении тетраэтиламмония (блокатор калия) фиксировали зависимость тока ионов натрия от времени, при введении тетродотоксина – зависимость тока ионов калия от времени. Зависимость 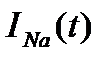 графически выражалась так, как показано на рис. 5. Графики1, 2 и 3 соответствовали различным значениям фиксированного потенциала. Для конкретности положим
графически выражалась так, как показано на рис. 5. Графики1, 2 и 3 соответствовали различным значениям фиксированного потенциала. Для конкретности положим  .
. менялся во времени, а это возможно лишь при условии, что проводимость
менялся во времени, а это возможно лишь при условии, что проводимость  являлась функцией времени:
являлась функцией времени:  .
.


