|
| К главе I.
|
| 1)
| Если матрицы  и и 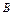 можно умножать, следует ли из этого, что их можно складывать? можно умножать, следует ли из этого, что их можно складывать?
|
| 2)
| Если матрицы 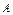 и и 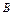 можно складывать, следует ли из этого, что их можно умножать? можно складывать, следует ли из этого, что их можно умножать?
|
| 3)
| Можно ли умножать квадратную матрицу на не квадратную?
|
| 4)
| Может ли произведение не квадратных матриц быть квадратной матрицей?
|
| 5)
| Может ли при умножении нулевых матриц получиться нулевая матрица?
|
| 6)
| Могут ли совпадать матрицы 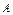 и и  ? ?
|
| 7)
| Как выглядит матрица 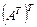 ? ?
|
| 8)
| Верно ли равенство 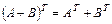 ? ?
|
| 9)
| Верно ли равенство 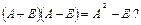
|
| 10)
| Верно ли равенство 
|
| 11)
| Верно ли равенство 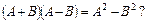
|
| 12)
| Верно ли равенство 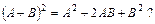
|
| 13)
| Обязательно ли существуют произведения 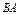 , если , если  ? ?
|
| 14)
| Может ли произведение матриц быть числом?
|
| 15)
| Как изменятся произведения матриц  и и 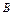 , если переставить , если переставить  -ю и -ю и  -ю строки матрицы -ю строки матрицы  ? ?
|
| 16)
| Как изменится произведение матриц  и и 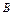 , если к , если к  -й строке матрицы А прибавить -й строке матрицы А прибавить  -ю строку, умноженную на число -ю строку, умноженную на число 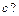
|
| 17)
| Как изменится произведение матриц  и и 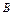 , если переставить , если переставить  -й и -й и  -й столбцы матрицы -й столбцы матрицы 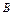 ? ?
|
| 18)
| Как изменится произведение матриц  и и 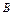 , если к , если к  -му столбцу матрицы В прибавить -му столбцу матрицы В прибавить  -й столбец, умноженный на число -й столбец, умноженный на число 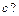
|
|
| К главе II.
|
| 19)
| Могут ли все алгебраические дополнения некоторой матрицы 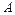 быть равны соответствующим минорам, т. е. быть равны соответствующим минорам, т. е. 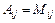 ? ?
|
| 20)
| Могут ли все алгебраические дополнения некоторой матрицы 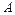 быть равны соответствующим минорам быть равны соответствующим минорам  ? ?
|
| 21)
| Могут ли все алгебраические дополнения некоторой матрицы 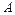 быть равны соответствующим
элементам быть равны соответствующим
элементам 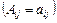 ? ?
|
| 22)
| Может ли определитель 2-го порядка принимать значение большее, чем определитель 5-го порядка?
|
| 23)
| Может ли определитель изменить знак на противоположный при транспонировании матрицы?
|
| 24)
| Дана квадратная матрица n-го порядка 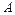 . Чему равна сумма . Чему равна сумма  ? ?
|
| 25)
| Можно ли вычислить миноры, дополнительные к элементам не квадратной матрицы?
|
| 26)
| Как изменится определитель 3-го порядка, если его строки переставить следующим образом: первую – на место второй, вторую – на место третьей, третью – на место первой?
|
| 27)
| Как изменится определитель n-го порядка, если его строки переставить следующим образом: первую – на место второй, вторую – на место третьей, …, 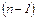 -ю – на место -ю – на место 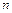 -й, -й, 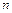 -ю – на место первой? -ю – на место первой?
|
| 28)
| Сколько всего миноров у квадратной матрицы 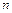 -го порядка? -го порядка?
|
| 29)
| К главе III.
|
| 30)
| Могут ли различные методы решения системы линейных уравнений (метод Крамера и метод обратной матрицы) дать различные ответы?
|
| 31)
| Возможно ли, чтобы система линейных уравнений имела решение с помощью метода Гаусса, но не имела бы решения по формулам Крамера?
|
| 32)
| В системе n линейных уравнений с n неизвестными поменяли местами два уравнения. Изменятся ли формы записи решения с помощью обратной матрицы и по формулам Крамера? Изменится ли общее решение?
|
| 33)
| Доказать, что формулы Крамера являются другой формой записи решения 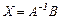 системы линейных уравнений системы линейных уравнений 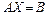
|
| 34)
| Решить систему линейных уравнений:

|
|
| К главе I.
|
| 1)
| Понятие функции. Числовые функции.
|
| 2)
| Способы задания функции.
|
| 3)
| График функции.
|
| 4)
| Периодичность.
|
| 5)
| Чётность и нечётность.
|
| 6)
| Монотонность.
|
| 7)
| Ограниченность.
|
| 8)
| Понятие сложной функции.
|
| 9)
| Элементарные функции.
|
| 10)
| Определение числовой последовательности.
|
| 11)
| Когда числовая последовательность считается заданной.
|
| 12)
| Свойства последовательностей.
|
| 13)
| Монотонные последовательности
|
| 14)
| Ограниченные и неограниченные последовательности.
|
| 15)
| Операции над числовыми последовательностями.
|
| 16)
| Предел последовательности.
|
| 17)
| Бесконечно большие и бесконечно малые последовательности.
|
| 18)
| Основные свойства сходящихся последовательностей.
|
| 19)
| Предел функции в точке.
|
| 20)
| Геометрический смысл предела функции в точке.
|
| 21)
| Предел функции на бесконечности (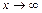 ). ).
|
| 22)
| Односторонние пределы.
|
| 23)
| Основные теоремы о пределах.
|
| 24)
| Замечательные пределы.
|
| 25)
| Непрерывность функции в точке.
|
| 26)
| Непрерывность функции на промежутке.
|
| 27)
| Классификация точек разрыва.
|
| 28)
| Основные теоремы о непрерывных функциях.
|
| 29)
| Свойства функций, непрерывных на отрезке.
|
|
| К главе II.
|
| 30)
| Понятие производной.
|
| 31)
| Геометрический смысл производной.
|
| 32)
| Механический смысл производной.
|
| 33)
| Связь между непрерывностью и дифференцируемостью функции.
|
| 34)
| Таблица производных основных элементарных функций.
|
| 35)
| Правила дифференцирования.
|
| 36)
| Дифференцирование сложных функций.
|
| 37)
| Производные высших порядков.
|
| 38)
| Основные теоремы дифференциального исчисления.
|
| 39)
| Правило Лопиталя.
|
|
| К главе III.
|
| 40)
| Понятие дифференциала функции.
|
| 41)
| Геометрический смысл дифференциала.
|
| 42)
| Техника вычисления дифференциалов.
|
| 43)
| Дифференциал 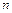 – го порядка. – го порядка.
|
| 44)
| Применение дифференциала к приближённым вычислениям.
|
|
| К главе IV.
|
| 45)
| Что называется интервалом монотонности функции?
|
| 46)
| Как применяется производная для нахождения интервалов монотонности функции?
|
| 47)
| Что называется экстремумом функции?
|
| 48)
| Как применяется производная для нахождения точек экстремума функции?
|
| 49)
| Как находятся наибольшее наименьшее значения функции на отрезке?
|
| 50)
| Что означают понятия «выпуклость» и «вогнутость» графика функции?
|
| 51)
| Как находятся интервалы выпуклости и вогнутости графика функции с помощью производной второго порядка?
|
| 52)
| Какая точка называется точкой перегиба?
|
| 53)
| Как находятся точки перегиба графика функции с помощью производной второго порядка?
|
| 54)
| По фрагменту графика функции охарактеризуйте возможные значения её производных первого и второго порядка в окрестности данной точки.
|
| 55)
| Что такое асимптота кривой?
|
| 56)
| Как находятся вертикальные и горизонтальные асимптоты графика функции?
|
| 57)
| Как находятся наклонные асимптоты графика функции?
|
| 58)
| Перечислите основные этапы полного исследования функции.
|