Цель работы: изучение геометрической оптики, определение фокусного расстояния собирающей линзы.
Приборы и принадлежности: источник света (лампа накаливания), линейка, набор линз, экран.
Теоретическая часть
Линзой называется прозрачное (чаще всего стеклянное) тело, ограниченное двумя криволинейными (обычно сферическими) поверхностями или одной криволинейной и одной плоской поверхностью.
На рис. 1 изображены поперечные сечения двояковыпуклой (а)и двояковогнутой (б)сферических линз (R1, R2 и R3 – радиусы кривизны их сферических поверхностей). Прямая SS', про 
ходящая через центры кривизны поверхностей, образующих линзу, называется главной оптической осью (или просто осью) линзы.
Мы будем рассматривать только
тонкие линзы, толщина С
1С
2 которых пренебрежимо мала по сравнению с радиусами кривизны линзы (рис. 1-2). Для тонких линз можно считать, что точки С
1 и С
2 сливаются в одну точку С – главный
оптический центр линзы, обладающий тем свойством, что проходящие через него лучи практически не преломляются линзой.
Если источник света S (рис. 3) находится на главной оптической оси, то его изображение S1 (действительное или мнимое) будет также лежать на главной оптической оси. Принято обозначать расстояние от светящейся точки до линзы через d, а от её изображения до линзы через f. При этом f считают положительным, если изображение действительное, и отрицательным, если изображение мнимое. В силу обратимости световых лучей расстояния d и f являются сопряженными.
Когда на собирающую линзу падает пучок лучей, параллельных главной оптической оси, то они сходятся за линзой в одной точке F (рис. 4а), называемой главным фокусом линзы, а расстояние от центра линзы С до F – главным фокусным расстоянием линзы. Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется главной фокальной плоскостью. Аналогичным образом вводится понятие фокуса и главного фокусного расстояния рассеивающей линзы (рис. 4б).
Выполнение работы основано на использовании формулы тонкой линзы:
 , (1)
, (1)
которую можно преобразовать к следующему удобному виду:
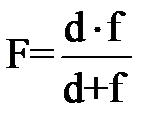 (2)
(2)


 , (1)
, (1)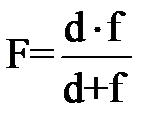 (2)
(2)


