Пусть заданы векторы в прямоугольной системе координат
Скалярное произведение векторов.
Определение. Скалярным произведением векторов
Свойства скалярного произведения:
1) 2) 3) 4) 5) (m
Если рассматривать векторы
Пример. Найти (5 10 т.к.
Пример. Найти угол между векторами
Т.е.
cosj =
Пример. Найти скалярное произведение (3 15 + 12×36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример. Найти угол между векторами
Т.е.
cosj =
Пример. При каком m векторы
Пример. Найти скалярное произведение векторов (
+ 27 + 51 + 135 + 72 + 252 = 547.
Векторное произведение векторов.
Определение. Векторным произведением векторов 1)
2) вектор 3) Обозначается:
j
Свойства векторного произведения векторов:
1) 2) 3) (m 4) 5) Если заданы векторы
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах
Пример. Найти векторное произведение векторов
При использовании компьютерной версии “ Курса высшей математики ” можно запустить программу, которая может найти скалярное и векторное произведения двух векторов. Для запуска программы дважды щелкните на значке:
В открывшемся окне программы введите координаты векторов и нажмите Enter. После получения скалярного произведения нажмите Enter еще раз – будет получено векторное произведение. Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
Пример. Доказать, что векторы
Пример. Найти площадь параллелограмма, построенного на векторах
Смешанное произведение векторов.
Определение. Смешанным произведением векторов Обозначается Смешанное произведение
Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю; б)два из векторов коллинеарны; в)векторы компланарны. 2) 3) 4) 5) Объем треугольной пирамиды, образованной векторами
6)Если
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости. Найдем координаты векторов: Найдем смешанное произведение полученных векторов:
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов: Объем пирамиды Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
Sосн = Т.к. V =
Уравнение поверхности в пространстве.
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
Общее уравнение плоскости.
Ax + By + Cz + D = 0, где А, В, С – координаты вектора
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz D = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = D = 0 – плоскость проходит через ось Ох В = D = 0 – плоскость проходит через ось Оу С = D = 0 – плоскость проходит через ось Oz А = В = D = 0 – плоскость совпадает с плоскостью хОу А = С = D = 0 – плоскость совпадает с плоскостью xOz В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
|

 тогда
тогда
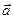 и
и 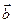 называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.
 ) =
) =  в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то
 Используя полученные равенства, получаем формулу для вычисления угла между векторами:
Используя полученные равенства, получаем формулу для вычисления угла между векторами: ;
;
 ,
, .
.
 .
. .
.



 .
. .
.
 и
и  перпендикулярны.
перпендикулярны.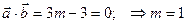 .
.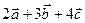 и
и  , если
, если 


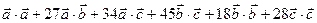 = 10 +
= 10 + , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: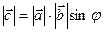 , где j - угол между векторами
, где j - угол между векторами 
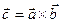 или
или  .
.
 ;
; , если
, если  , то
, то

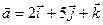 и
и .
. .
.



 (ед2).
(ед2). ,
,  и
и  компланарны.
компланарны. , т.к. векторы линейно зависимы, то они компланарны.
, т.к. векторы линейно зависимы, то они компланарны. , если
, если 
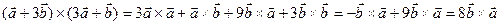
 (ед2).
(ед2). или (
или (





 ,
,  , то
, то

 ,
,



 (ед2)
(ед2) ;
;  (ед)
(ед) Определение. Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению:
Определение. Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: -вектор нормали к плоскости.
-вектор нормали к плоскости.


