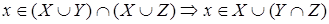 ,
,
откуда вытекает, что
 ,
,
что и требовалось доказать.
Из (1.6) вытекает, что
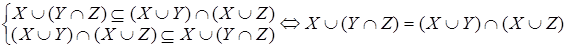 ,
,
что и требовалось доказать.
Упорядоченной 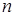 -кой
-кой  называется запись вида
называется запись вида
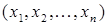 .
.
Замечание 1.10. Содержательно, эта запись означает, что элемент  записан на
записан на  -м месте, элемент
-м месте, элемент  – на
– на  -м месте, …, элемент
-м месте, …, элемент  – на
– на 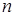 -м месте, т.е. элементы
-м месте, т.е. элементы 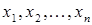 записаны в фиксированном порядке. Таким образом, понятие упорядоченная
записаны в фиксированном порядке. Таким образом, понятие упорядоченная 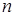 -ка – это аналог классического понятия вектор, заданный своими координатами в математике (в отличие от вектора компоненты
-ка – это аналог классического понятия вектор, заданный своими координатами в математике (в отличие от вектора компоненты 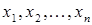 упорядоченной
упорядоченной 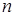 -ки – элементы любого, не обязательно числового, множества) или понятия список, содержащий
-ки – элементы любого, не обязательно числового, множества) или понятия список, содержащий 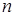 элементов в программировании.
элементов в программировании.
Декартовым произведением множеств 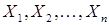
 (обозначается
(обозначается  ) называется множество, состоящее из всех упорядоченных
) называется множество, состоящее из всех упорядоченных 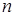 -ок
-ок 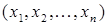 , где
, где  ,
, 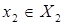 , …
, … 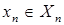 , т.е.
, т.е.
 .
.
Если  , то множество
, то множество
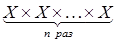
называется 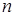 -й декартовой степенью множества
-й декартовой степенью множества  и обозначается
и обозначается  . По определению полагают
. По определению полагают
 ,
, 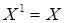 .
.
Важный специальный случай декартового произведения имеет место при 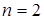 . Запись
. Запись  называется упорядоченной парой, а декартово произведение двух множеств
называется упорядоченной парой, а декартово произведение двух множеств  и
и 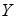 определяется равенством
определяется равенством
 . (1.30)
. (1.30)
Декартово произведение двух множеств можно представить графически (см. рис. 1.3). Для этого от одной и той же точки откладывают горизонтальный и вертикальный отрезки и на них, как на сторонах, строится прямоугольник. Горизонтальный отрезок представляет множество  , а вертикальный отрезок – множество
, а вертикальный отрезок – множество 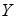 . В соответствии с (1.30), декартово произведение
. В соответствии с (1.30), декартово произведение 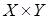 представляется частью плоскости, ограниченной построенным прямоугольником (включая его границу), т.е. элементы множества
представляется частью плоскости, ограниченной построенным прямоугольником (включая его границу), т.е. элементы множества 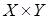 представляются точками плоскости, а пара
представляются точками плоскости, а пара  интерпретируется как координаты соответствующей точки.
интерпретируется как координаты соответствующей точки.
 Замечание 1.11. С математической точки зрения в настоящем пункте построена алгебра. Одно из центральных понятий современной математики – алгебра – формально определяется как упорядоченная пара
Замечание 1.11. С математической точки зрения в настоящем пункте построена алгебра. Одно из центральных понятий современной математики – алгебра – формально определяется как упорядоченная пара  , где
, где  – множество элементов (носитель алгебры
– множество элементов (носитель алгебры  ), а
), а  – множество операций (сигнатура алгебры
– множество операций (сигнатура алгебры  ). Элемент
). Элемент  называется
называется 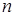 - арной (возможно, частичной) операцией
- арной (возможно, частичной) операцией 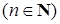 , если каждой упорядоченной
, если каждой упорядоченной 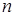 -ке
-ке 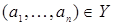
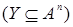 , поставлен в соответствие однозначно определенный элемент
, поставлен в соответствие однозначно определенный элемент  – результат операции
– результат операции 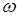 (это свойство – замкнутость операции
(это свойство – замкнутость операции 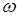 на множестве
на множестве  ). 1-арную, 2-арную и 3-арную операции называют, соответственно, унарной, бинарной и тернарной операциями. Иногда в множестве
). 1-арную, 2-арную и 3-арную операции называют, соответственно, унарной, бинарной и тернарной операциями. Иногда в множестве  выделяют некоторые элементы. Их называют
выделяют некоторые элементы. Их называют 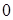 -арными операциями. Таким образом, упорядоченная пара
-арными операциями. Таким образом, упорядоченная пара 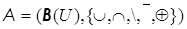 – алгебра множеств (
– алгебра множеств ( – универсальное множество).
– универсальное множество).
Упорядоченная пара 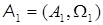 – подалгебра алгебры
– подалгебра алгебры  , если
, если 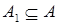 ,
, 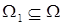 и каждая операция
и каждая операция 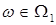 замкнута на множестве
замкнута на множестве  . Подалгебра
. Подалгебра  алгебры множеств – булева алгебра множеств – представляет собой специальный случай следующего общего математического понятия. Алгебра
алгебры множеств – булева алгебра множеств – представляет собой специальный случай следующего общего математического понятия. Алгебра  – булева (
– булева (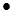 ,
,  – бинарные, а ~ – унарная операции), если выполнены следующие условия (
– бинарные, а ~ – унарная операции), если выполнены следующие условия (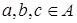 ):
):
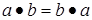 ,
, 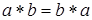 (коммутативность);
(коммутативность);
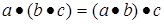 ,
, 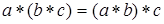 (ассоциативность);
(ассоциативность);
 ,
, 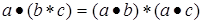 (дистрибутивность);
(дистрибутивность);
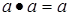 ,
,  (идемпотентность);
(идемпотентность);
 (совместимость);
(совместимость);
существуют такие элементы 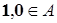 , что для всех
, что для всех 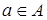
 ,
,  ,
,  ,
,  .
.
для каждого 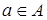 существует такой элемент
существует такой элемент 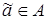 (
( – дополнение элемента
– дополнение элемента 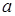 ), что
), что
 ,
,  .
.
Все остальные свойства операций, и ~, аналогичные свойствам операций, и для множеств, могут быть выведены формальными методами (т.е. доказаны, как теоремы) из перечисленных выше свойств 1)-7).

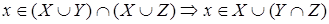 ,
, ,
,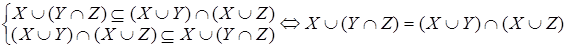 ,
,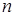 -кой
-кой  называется запись вида
называется запись вида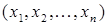 .
. записан на
записан на  -м месте, элемент
-м месте, элемент  – на
– на  -м месте, …, элемент
-м месте, …, элемент  – на
– на 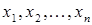 записаны в фиксированном порядке. Таким образом, понятие упорядоченная
записаны в фиксированном порядке. Таким образом, понятие упорядоченная 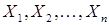
 ) называется множество, состоящее из всех упорядоченных
) называется множество, состоящее из всех упорядоченных  ,
, 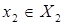 , …
, … 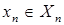 , т.е.
, т.е. .
. , то множество
, то множество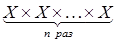
 и обозначается
и обозначается  . По определению полагают
. По определению полагают ,
, 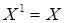 .
.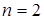 . Запись
. Запись  называется упорядоченной парой, а декартово произведение двух множеств
называется упорядоченной парой, а декартово произведение двух множеств 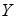 определяется равенством
определяется равенством . (1.30)
. (1.30)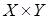 представляется частью плоскости, ограниченной построенным прямоугольником (включая его границу), т.е. элементы множества
представляется частью плоскости, ограниченной построенным прямоугольником (включая его границу), т.е. элементы множества  Замечание 1.11. С математической точки зрения в настоящем пункте построена алгебра. Одно из центральных понятий современной математики – алгебра – формально определяется как упорядоченная пара
Замечание 1.11. С математической точки зрения в настоящем пункте построена алгебра. Одно из центральных понятий современной математики – алгебра – формально определяется как упорядоченная пара  , где
, где  – множество элементов (носитель алгебры
– множество элементов (носитель алгебры  ), а
), а  – множество операций (сигнатура алгебры
– множество операций (сигнатура алгебры  называется
называется 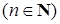 , если каждой упорядоченной
, если каждой упорядоченной 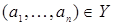
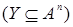 , поставлен в соответствие однозначно определенный элемент
, поставлен в соответствие однозначно определенный элемент  – результат операции
– результат операции 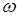 (это свойство – замкнутость операции
(это свойство – замкнутость операции  ). 1-арную, 2-арную и 3-арную операции называют, соответственно, унарной, бинарной и тернарной операциями. Иногда в множестве
). 1-арную, 2-арную и 3-арную операции называют, соответственно, унарной, бинарной и тернарной операциями. Иногда в множестве 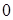 -арными операциями. Таким образом, упорядоченная пара
-арными операциями. Таким образом, упорядоченная пара 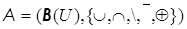 – алгебра множеств (
– алгебра множеств ( – универсальное множество).
– универсальное множество).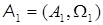 – подалгебра алгебры
– подалгебра алгебры 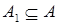 ,
, 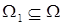 и каждая операция
и каждая операция 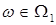 замкнута на множестве
замкнута на множестве  . Подалгебра
. Подалгебра  алгебры множеств – булева алгебра множеств – представляет собой специальный случай следующего общего математического понятия. Алгебра
алгебры множеств – булева алгебра множеств – представляет собой специальный случай следующего общего математического понятия. Алгебра  – булева (
– булева ( ,
,  – бинарные, а ~ – унарная операции), если выполнены следующие условия (
– бинарные, а ~ – унарная операции), если выполнены следующие условия (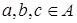 ):
):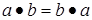 ,
, 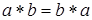 (коммутативность);
(коммутативность);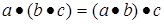 ,
, 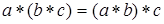 (ассоциативность);
(ассоциативность); ,
, 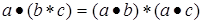 (дистрибутивность);
(дистрибутивность);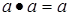 ,
,  (идемпотентность);
(идемпотентность); (совместимость);
(совместимость);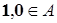 , что для всех
, что для всех 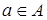
 ,
,  ,
,  ,
,  .
.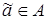 (
( – дополнение элемента
– дополнение элемента 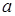 ), что
), что ,
,  .
.


