МНОЖЕСТВА.
Понятие множество – фундаментальное понятие математики – дает возможность рассматривать совокупность объектов как единое целое. Теория множеств, как самостоятельный раздел математики, сформировалась в XIX-ом веке. Ее основоположник – немецкий математик Георг Кантор. Значение теории множеств обусловлено тем, что она дает универсальный язык, позволяющий с единых позиций описывать конструкции и процессы, как в самой математике, так и в многочисленных ее приложениях. В связи с созданием вычислительной техники резко возрос интерес к использованию дискретных моделей. Эти модели, по своей сути, представляют собой набор множеств и отношений между ними. Поэтому аппарат теории множеств является основным средством исследования дискретных моделей.
Основные понятия и определения.
В качестве исходных понятий выбираются множество и элемент. По этой причине эти понятия не определяются. Принято считать, что множество состоит из различимых между собой элементов. Синонимы слова множество – совокупность, класс, коллекция, собрание, список и т.д.
Пример 1.1. 1.Множествами из окружающей нас действительности являются: множество учебных корпусов ДонНУ, множество факультетов ДонНУ, множество студентов математического факультета ДонНУ, множество магазинов на ул. Артема, множество стран в Европе и т.д.;
2. Множествами из курса школьной математики являются: множество точек данной прямой, множество делителей данного числа, множество корней данного уравнения и т.д.
В настоящем разделе будем обозначать множества прописными, а их элементы – строчными латинскими буквами. При необходимости будем использовать индексы. Итак, множества обозначаем буквами  , а элементы – буквами
, а элементы – буквами  .
.
Замечание 1.1. Для тех множеств, которые часто применяются в математике, введены специальные обозначения. К ним относятся:
 – множество натуральных (т.е. целых положительных) чисел;
– множество натуральных (т.е. целых положительных) чисел;
 ,
,  и
и  – множества, соответственно, целых, неотрицательных целых и неположительных целых чисел;
– множества, соответственно, целых, неотрицательных целых и неположительных целых чисел;

 – множество чисел
– множество чисел  ;
;
 – множество рациональных чисел, т.е. дробей вида
– множество рациональных чисел, т.е. дробей вида 
 ;
;
 и
и  – множества рациональных, соответственно, неотрицательных и неположительных чисел;
– множества рациональных, соответственно, неотрицательных и неположительных чисел;
 ,
,  и
и  – множества, соответственно, действительных, неотрицательных действительных и неположительных действительных чисел.
– множества, соответственно, действительных, неотрицательных действительных и неположительных действительных чисел.
Запись 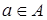 означает утверждение ‘
означает утверждение ‘ 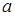 – элемент множества
– элемент множества  ’, а запись
’, а запись  – утверждение ‘
– утверждение ‘ 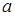 не является элементом множества
не является элементом множества  ’. В случае, когда
’. В случае, когда 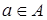 говорят также, что ‘
говорят также, что ‘ 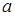 принадлежит
принадлежит  ’, а в случае, когда
’, а в случае, когда  – что ‘
– что ‘ 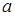 не принадлежит
не принадлежит  ’.
’.
Множества  и
и 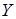 называются равными (обозначается
называются равными (обозначается  ), если они состоят из одних и тех же элементов. Из этого определения непосредственно вытекает, что:
), если они состоят из одних и тех же элементов. Из этого определения непосредственно вытекает, что:
1.  для любого множества
для любого множества  ;
;
2. если  , то
, то  для любых множеств
для любых множеств  и
и 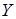 ;
;
3. если  и
и  , то
, то  для любых множеств
для любых множеств  ,
, 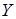 и
и  .
.
Для краткости записи будем использовать следующую стандартную математическую символику:
 – утверждение ‘ если
– утверждение ‘ если  , то
, то  ’;
’;
 – утверждение ‘
– утверждение ‘  тогда и только тогда, когда
тогда и только тогда, когда  ’;
’;
 – утверждение ‘ для всех
– утверждение ‘ для всех  утверждение
утверждение  – истинное ’;
– истинное ’;
 – утверждение ‘ существует такое
– утверждение ‘ существует такое  , что утверждение
, что утверждение  – истинное ’.
– истинное ’.
Отметим, что символы  и
и  называются квантором, соответственно, всеобщности и существования.
называются квантором, соответственно, всеобщности и существования.
С помощью введенной символики, три перечисленные выше свойства равенства множеств можно записать в виде
 , (1.1)
, (1.1)
 , (1.2)
, (1.2)
 . (1.3)
. (1.3)
В дальнейшем в формулах типа (1.3) вместо союза и используется символ  , а вместо союза или – символ
, а вместо союза или – символ  .
.
Запись  означает, что множества
означает, что множества  и
и 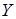 не равны друг другу. Это означает, что существует элемент, принадлежащий одному из этих множеств и не принадлежащий другому. Таким образом,
не равны друг другу. Это означает, что существует элемент, принадлежащий одному из этих множеств и не принадлежащий другому. Таким образом,
 .
.
В дальнейшем для утверждений вида
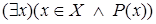 ,
,  ,
,
 ,
, 
используются, соответственно, записи
 ,
,  ,
,
 ,
,  .
.
Таким образом,
 .
.
Множество называется пустым, если оно не содержит ни одного элемента.
Пример 1.2. Каждое из следующих множеств – пустое: 1) множество корней уравнения  ; 2) множество океанов на Земле, площадь которых больше площади Тихого океана; 3) множество натуральных чисел, меньших, числа
; 2) множество океанов на Земле, площадь которых больше площади Тихого океана; 3) множество натуральных чисел, меньших, числа  .
.
Все пустые множества считаются равными друг другу. Поэтому, для пустого множества используется стандартное обозначение  .
.
Если каждый элемент множества  является также элементом множества
является также элементом множества 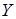 , то говорят, что
, то говорят, что  содержится (или включается) в
содержится (или включается) в 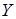 . В этом случае пишут
. В этом случае пишут  . Таким образом,
. Таким образом,
 . (1.4)
. (1.4)
Запись  означает: не верно, что
означает: не верно, что  . В этом случае также говорят, что
. В этом случае также говорят, что  не содержится (или не включается) в
не содержится (или не включается) в 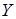 . При определении символа
. При определении символа  (а также символов
(а также символов  и
и  ) используется конструкция вида
) используется конструкция вида
не верно, что утверждение  – истинное.
– истинное.
Такая конструкция называется отрицанием  и обозначается
и обозначается  (читается не
(читается не  ). Действие отрицания
). Действие отрицания  на кванторы осуществляется в соответствии с формулами
на кванторы осуществляется в соответствии с формулами
 ,
,
 .
.
Таким образом,
 .
.
Из (1.4) вытекает, что
 , (1.5)
, (1.5)
 , (1.6)
, (1.6)
 , (1.7)
, (1.7)
 , (1.8)
, (1.8)
 . (1.9)
. (1.9)
Замечание 1.2. Утверждение (1.6) дает универсальный метод доказательства равенства двух множеств, а именно: для доказательства равенства  достаточно доказать, что оба включения
достаточно доказать, что оба включения  и
и  – истинные.
– истинные.
Если  , то множество
, то множество  называется подмножеством множества
называется подмножеством множества 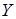 . Из (1.5) и (1.9) вытекает, что подмножествами любого множества
. Из (1.5) и (1.9) вытекает, что подмножествами любого множества  являются
являются  и
и  . Эти подмножества называются несобственными подмножествами множества
. Эти подмножества называются несобственными подмножествами множества  . Все остальные подмножества множества
. Все остальные подмножества множества  (если такие существуют) – собственные подмножества множества
(если такие существуют) – собственные подмножества множества  .
.
Понятие подмножество дает возможность сопоставить с каждым множеством  множество
множество  , состоящее из всех подмножеств множества
, состоящее из всех подмножеств множества  . Множество
. Множество  называется булеаном множества
называется булеаном множества  (иногда для обозначения булеана множества
(иногда для обозначения булеана множества  используется символ
используется символ  ).
).
Если  и
и  (причем последнее хотят подчеркнуть в явном виде), то говорят, что
(причем последнее хотят подчеркнуть в явном виде), то говорят, что  строго содержится (или включается) в
строго содержится (или включается) в 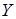 и пишут
и пишут  (запись
(запись  – отрицание утверждения
– отрицание утверждения  ). Итак,
). Итак,
 . (1.10)
. (1.10)
Из этого определения вытекает, что
 , (1.11)
, (1.11)
 , (1.12)
, (1.12)
 . (1.13)
. (1.13)
Замечание 1.3. В силу (1.10) для доказательства строгого включения  достаточно установить, что включение
достаточно установить, что включение  – истинное и, кроме того, показать, что существует элемент множества
– истинное и, кроме того, показать, что существует элемент множества 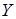 , не принадлежащий множеству
, не принадлежащий множеству  .
.
Включения  и
и  определяются следующим образом
определяются следующим образом
 , (1.14)
, (1.14)
 . (1.15)
. (1.15)
Подчеркнем, что запись вида  (где
(где  – любой из символов
– любой из символов  ,
,  ,
,  и
и  ) означает, что не имеет места включение
) означает, что не имеет места включение  .
.
Множество, состоящее из конечного числа элементов, называется конечным, а множество, состоящее из бесконечного числа элементов – бесконечным. Конечное множество можно задать перечислением всех его элементов. Для этого используется запись вида  , т.е. все принадлежащие множеству
, т.е. все принадлежащие множеству  элементы записываются (в произвольном порядке) в явном виде и заключаются в фигурные скобки. Такая запись – громоздкая, если число
элементы записываются (в произвольном порядке) в явном виде и заключаются в фигурные скобки. Такая запись – громоздкая, если число 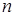 и вообще не приемлема, если множество
и вообще не приемлема, если множество  – бесконечное. В указанных случаях множество может быть задано с помощью характеристического свойства, т.е. свойства, которым обладает каждый элемент множества и не обладает ни один элемент, не принадлежащий этому множеству.
– бесконечное. В указанных случаях множество может быть задано с помощью характеристического свойства, т.е. свойства, которым обладает каждый элемент множества и не обладает ни один элемент, не принадлежащий этому множеству.
Замечание 1.4. Одно и то же множество можно задать различными характеристическими свойствами.
Пример 1.3. Пусть  . Тогда: 1)
. Тогда: 1)  – множество натуральных четных чисел, удовлетворяющих неравенству
– множество натуральных четных чисел, удовлетворяющих неравенству  ; 2)
; 2)  – множество корней уравнения
– множество корней уравнения  и т.д.
и т.д.
Чтобы задать множество  с помощью характеристического свойства необходимо построить отображение
с помощью характеристического свойства необходимо построить отображение
 ,
,
называемое характеристической функцией множества  , после чего используется запись вида
, после чего используется запись вида  .
.
Пример 1.4. 1. Множество  из примера 1.3 может быть задано следуюшим образом:
из примера 1.3 может быть задано следуюшим образом:  ,
,  (запись
(запись  – утверждение ‘число
– утверждение ‘число 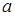 делится на число
делится на число  ’) и т.д.
’) и т.д.
2. Пусть  ,
,  ,
,  ,
,  ,
,  .
.
Тогда  и истинны следующие утверждения относительно включений множеств:
и истинны следующие утверждения относительно включений множеств:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
В заключение отметим, что бесконечная последовательность чисел
 , (1.16)
, (1.16)
где  – формула общего члена, однозначно определяет множество
– формула общего члена, однозначно определяет множество
 .
.
Однако, если известно только конечное число членов последовательности (1.16), а формула ее общего члена  не известна, то в принципе невозможно однозначно определить множество
не известна, то в принципе невозможно однозначно определить множество  . Причина состоит в том, что существуют различные множества, которым принадлежат числа из заданной конечной части последовательности.
. Причина состоит в том, что существуют различные множества, которым принадлежат числа из заданной конечной части последовательности.
Пример 1.5. Числа  – элементы множеств
– элементы множеств  ,
,  и т.д.
и т.д.
Операции над множествами.
Предназначение операций над множествами состоит в том, чтобы получать новые множества из исходных. Одна из таких операций – операция  – была определена в п.1.1. Результатом применения операции
– была определена в п.1.1. Результатом применения операции  к множеству
к множеству  является множество, элементы которого – все подмножества множества
является множество, элементы которого – все подмножества множества  , т.е.
, т.е.  . Рассмотрим операции, которые принято считать основными операциями над множествами.
. Рассмотрим операции, которые принято считать основными операциями над множествами.
Объединением множеств  и
и 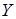 (обозначается
(обозначается  ) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств
) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств  и
и 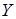 , т.е.
, т.е.
 . (1.17)
. (1.17)
Пересечением множеств  и
и 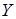 (обозначается
(обозначается  ) называется множество, состоящее из всех элементов, принадлежащих каждому из множеств
) называется множество, состоящее из всех элементов, принадлежащих каждому из множеств  и
и 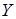 , т.е.
, т.е.
 . (1.18)
. (1.18)
Разностью множеств  и
и 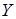 (обозначается
(обозначается  ) называется множество, состоящее из всех элементов множества
) называется множество, состоящее из всех элементов множества  , не принадлежащих множеству
, не принадлежащих множеству 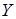 , т.е.
, т.е.
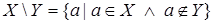 . (1.19)
. (1.19)
Достаточно часто встречается ситуация, когда все рассматриваемые множества конструируются из элементов одного и того же фиксированного множества  . Такое множество
. Такое множество  называется универсальным.
называется универсальным.
Пример 1.6. В процессе изучения планиметриигеометрические фигуры определяются как множества тех или иных точек плоскости. Таким образом, для планиметрии универсальным множеством  является множество всех точек плоскости.
является множество всех точек плоскости.
Дополнением множества  в универсальном множестве
в универсальном множестве  (обозначается
(обозначается 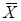 ) называется множество, состоящее из всех элементов (универсального множества
) называется множество, состоящее из всех элементов (универсального множества  ), не принадлежащих множеству
), не принадлежащих множеству  , т.е.
, т.е.
 . (1.20)
. (1.20)
Замечание 1.5. В каждом конкретном случае универсальное множество  фиксировано. Поэтому о множестве
фиксировано. Поэтому о множестве 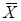 говорят дополнение множества
говорят дополнение множества  , а фразу в универсальном множестве
, а фразу в универсальном множестве  опускают.
опускают.
Симметрической разностью множеств  и
и 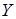 (обозначается
(обозначается  ) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
 . (1.21)
. (1.21)
Пример 1.7. Пусть  ,
,  , а универсальным множеством является
, а универсальным множеством является  . Тогда
. Тогда
 ,
,  ,
,  ,
,
 ,
,
 ,
,
 ,
,

 .
.
Операции над множествами можно иллюстрировать графически с помощью кругов Эйлера (их также называют диаграммами Венна). При такой иллюстрации исходные множества изображают кругами, а множество-результат выделяют штриховкой. Иллюстрация определенных выше операций над множествами дана на рис. 1.1.
Операции над множествами дают возможность представлять множества формулами. Это понятие определяется следующим образом: 1) каждый символ, обозначающий множество – формула; 2) если  и
и  – формулы, то
– формулы, то  ,
,  ,
,  ,
,  и
и  – формулы; 3) нет правил построения формул, отличающихся от 1) и 2).
– формулы; 3) нет правил построения формул, отличающихся от 1) и 2).
Пусть  – формула, содержащая обозначения множеств
– формула, содержащая обозначения множеств  . Выполнив все входящие в формулу
. Выполнив все входящие в формулу  операции над множествами, получим некоторое множество
операции над множествами, получим некоторое множество  . Говорят, что это множество
. Говорят, что это множество  определяется (или, иными словами, представлено) формулой
определяется (или, иными словами, представлено) формулой  .
.

Замечание 1.6. С целью упрощения записи формул принято руководствоваться следующим правилом экономии (т.е. удаления лишних) скобок: 1) если скобки отсутствуют, то приоритет операций (т.е. порядок их выполнения) определяется последовательностью:  , \,
, \,  ,
,  ,
,  ; 2) если скобки отсутствуют и необходимо выполнить одну и ту же операцию, то порядок ее выполнения – слева направо.
; 2) если скобки отсутствуют и необходимо выполнить одну и ту же операцию, то порядок ее выполнения – слева направо.
Пример 1.8. 1. Построим множество  : 1) строим множество
: 1) строим множество  ; 2) строим множество
; 2) строим множество  ; 3) строим множество
; 3) строим множество  ; 4) строим множество
; 4) строим множество  ; 5) строим множество
; 5) строим множество  .
.
2. Построим множество  : 1) строим множество
: 1) строим множество  ; 2) строим множество
; 2) строим множество  ; 3) строим множество
; 3) строим множество  ; 4) строим множество
; 4) строим множество  ; 5) строим множество
; 5) строим множество  .
.
Пусть  и
и  – формулы, построенные с использованием переменных
– формулы, построенные с использованием переменных  , обозначающих множества. Формулы
, обозначающих множества. Формулы  и
и  называются эквивалентными, если представленные ими множества равны друг другу при любых значениях переменных
называются эквивалентными, если представленные ими множества равны друг другу при любых значениях переменных  (отметим, что значениями переменных
(отметим, что значениями переменных  являются множества). В тех случаях, когда формулы
являются множества). В тех случаях, когда формулы  и
и  – эквивалентные, равенство
– эквивалентные, равенство  называется тождеством.
называется тождеством.
Замечание 1.7. Для равенства  существуют три возможности: 1) равенство
существуют три возможности: 1) равенство  – истинное для любых значений входящих в него переменных, т.е. равенство
– истинное для любых значений входящих в него переменных, т.е. равенство  – тождество; 2) равенство
– тождество; 2) равенство  – ложное для любых значений входящих в него переменных; 3) при одних значениях переменных равенство
– ложное для любых значений входящих в него переменных; 3) при одних значениях переменных равенство  – истинное, а при других значениях переменных равенство
– истинное, а при других значениях переменных равенство  – ложное.
– ложное.
Представление множества часто можно упростить последовательной заменой формул на эквивалентные. Перечислим основные тождества.
Идемпотентность:
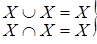 . (1.22)
. (1.22)
Коммутативность:
 . (1.23)
. (1.23)
Ассоциативность:
 . (1.24)
. (1.24)
Замечание 1.8. Тождества (1.24) дают возможность использовать бесскобочные записи  ,
,  ,
,  или в компактном виде, соответственно, записи
или в компактном виде, соответственно, записи  ,
,  ,
,  .
.
Дистрибутивность:
 . (1.25)
. (1.25)
Поглощение:
 . (1.26)
. (1.26)
Инволюция:
 . (1.27)
. (1.27)
Правила де Моргана:
 . (1.28)
. (1.28)
Свойства универсального и пустого множеств:
 . (1.29)
. (1.29)
Для того чтобы проверить, является ли равенство  тождеством, можно воспользоваться кругами Эйлера. Для этого на отдельных рисунках изображаются множества, представленные формулами
тождеством, можно воспользоваться кругами Эйлера. Для этого на отдельных рисунках изображаются множества, представленные формулами  и
и  . Если эти множества совпадают, то
. Если эти множества совпадают, то  – тождество. Если же построенные множества – различные, то равенство
– тождество. Если же построенные множества – различные, то равенство  не является тождеством.
не является тождеством.
Замечание 1.9. Проверка равенства  с помощью кругов Эйлера не является доказательством. Формальное доказательство того, что
с помощью кругов Эйлера не является доказательством. Формальное доказательство того, что  – тождество всегда можно осуществить в соответствии с формулой (1.6) (см. замечание 1.2).
– тождество всегда можно осуществить в соответствии с формулой (1.6) (см. замечание 1.2).
Пример 1.9. Проверим с помощью кругов Эйлера, являются ли тождествами равенства
 , (*)
, (*)
 . (**)
. (**)
На рис. 1.2 а) и б) изображены множества, представленные, соответственно, левой и правой частями равенства (*). Сравнивая эти рисунки, заключаем, что множества – равные. Следовательно, равенство (*) – тождество.
На рис. 1.2 в) и г) изображены множества, представленные, соответственно, левой и правой частями равенства (**). Сравнивая эти рисунки, заключаем, что множества – различные. Следовательно, равенство (*) не является тождеством.
Пример 1.10. Докажем, что формула (*) – тождество.
1. Докажем, что истинным является включение
 .
.
Пусть  . Тогда
. Тогда  или
или  . Рассмотрим эти случаи:
. Рассмотрим эти случаи:
 ,
,
 .
.

 , а элементы – буквами
, а элементы – буквами  .
. – множество натуральных (т.е. целых положительных) чисел;
– множество натуральных (т.е. целых положительных) чисел; ,
,  и
и  – множества, соответственно, целых, неотрицательных целых и неположительных целых чисел;
– множества, соответственно, целых, неотрицательных целых и неположительных целых чисел;
 – множество чисел
– множество чисел  ;
; – множество рациональных чисел, т.е. дробей вида
– множество рациональных чисел, т.е. дробей вида 
 ;
; и
и  – множества рациональных, соответственно, неотрицательных и неположительных чисел;
– множества рациональных, соответственно, неотрицательных и неположительных чисел; ,
,  и
и  – множества, соответственно, действительных, неотрицательных действительных и неположительных действительных чисел.
– множества, соответственно, действительных, неотрицательных действительных и неположительных действительных чисел.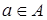 означает утверждение ‘
означает утверждение ‘ 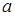 – элемент множества
– элемент множества  ’, а запись
’, а запись  – утверждение ‘
– утверждение ‘  и
и 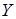 называются равными (обозначается
называются равными (обозначается  ), если они состоят из одних и тех же элементов. Из этого определения непосредственно вытекает, что:
), если они состоят из одних и тех же элементов. Из этого определения непосредственно вытекает, что: для любого множества
для любого множества  для любых множеств
для любых множеств  , то
, то  для любых множеств
для любых множеств  .
. – утверждение ‘ если
– утверждение ‘ если  , то
, то  ’;
’; – утверждение ‘
– утверждение ‘  – утверждение ‘ для всех
– утверждение ‘ для всех  утверждение
утверждение  – истинное ’;
– истинное ’; – утверждение ‘ существует такое
– утверждение ‘ существует такое  и
и  называются квантором, соответственно, всеобщности и существования.
называются квантором, соответственно, всеобщности и существования. , (1.1)
, (1.1) , (1.2)
, (1.2) . (1.3)
. (1.3) , а вместо союза или – символ
, а вместо союза или – символ  .
. означает, что множества
означает, что множества  .
.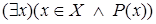 ,
,  ,
, ,
, 
 ,
,  ,
, ,
,  .
. .
. ; 2) множество океанов на Земле, площадь которых больше площади Тихого океана; 3) множество натуральных чисел, меньших, числа
; 2) множество океанов на Земле, площадь которых больше площади Тихого океана; 3) множество натуральных чисел, меньших, числа  .
. .
. . Таким образом,
. Таким образом, . (1.4)
. (1.4) означает: не верно, что
означает: не верно, что  (а также символов
(а также символов  и
и  ) используется конструкция вида
) используется конструкция вида (читается не
(читается не  на кванторы осуществляется в соответствии с формулами
на кванторы осуществляется в соответствии с формулами ,
, .
. .
. , (1.5)
, (1.5) , (1.6)
, (1.6) , (1.7)
, (1.7) , (1.8)
, (1.8) . (1.9)
. (1.9) – истинные.
– истинные. , состоящее из всех подмножеств множества
, состоящее из всех подмножеств множества  ).
). (запись
(запись  – отрицание утверждения
– отрицание утверждения  . (1.10)
. (1.10) , (1.11)
, (1.11) , (1.12)
, (1.12) . (1.13)
. (1.13) и
и  определяются следующим образом
определяются следующим образом , (1.14)
, (1.14) . (1.15)
. (1.15) (где
(где  – любой из символов
– любой из символов  ,
,  ,
,  .
. , т.е. все принадлежащие множеству
, т.е. все принадлежащие множеству  и вообще не приемлема, если множество
и вообще не приемлема, если множество  . Тогда: 1)
. Тогда: 1)  ; 2)
; 2)  и т.д.
и т.д. ,
, .
. ,
,  (запись
(запись  – утверждение ‘число
– утверждение ‘число  ’) и т.д.
’) и т.д. ,
,  ,
,  ,
,  ,
,  .
. и истинны следующие утверждения относительно включений множеств:
и истинны следующие утверждения относительно включений множеств:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. , (1.16)
, (1.16) – формула общего члена, однозначно определяет множество
– формула общего члена, однозначно определяет множество .
. . Причина состоит в том, что существуют различные множества, которым принадлежат числа из заданной конечной части последовательности.
. Причина состоит в том, что существуют различные множества, которым принадлежат числа из заданной конечной части последовательности. – элементы множеств
– элементы множеств  ,
,  и т.д.
и т.д. – была определена в п.1.1. Результатом применения операции
– была определена в п.1.1. Результатом применения операции  . Рассмотрим операции, которые принято считать основными операциями над множествами.
. Рассмотрим операции, которые принято считать основными операциями над множествами. ) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств
) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств  . (1.17)
. (1.17) ) называется множество, состоящее из всех элементов, принадлежащих каждому из множеств
) называется множество, состоящее из всех элементов, принадлежащих каждому из множеств  . (1.18)
. (1.18) ) называется множество, состоящее из всех элементов множества
) называется множество, состоящее из всех элементов множества 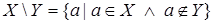 . (1.19)
. (1.19) . Такое множество
. Такое множество 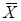 ) называется множество, состоящее из всех элементов (универсального множества
) называется множество, состоящее из всех элементов (универсального множества  . (1.20)
. (1.20) ) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е. . (1.21)
. (1.21) ,
,  , а универсальным множеством является
, а универсальным множеством является  ,
,  ,
,  ,
, ,
, ,
, ,
,
 .
. и
и  – формулы, то
– формулы, то  ,
,  ,
,  ,
,  и
и  – формулы; 3) нет правил построения формул, отличающихся от 1) и 2).
– формулы; 3) нет правил построения формул, отличающихся от 1) и 2). – формула, содержащая обозначения множеств
– формула, содержащая обозначения множеств  . Выполнив все входящие в формулу
. Выполнив все входящие в формулу 
 , \,
, \,  ,
,  ,
,  ; 2) если скобки отсутствуют и необходимо выполнить одну и ту же операцию, то порядок ее выполнения – слева направо.
; 2) если скобки отсутствуют и необходимо выполнить одну и ту же операцию, то порядок ее выполнения – слева направо. : 1) строим множество
: 1) строим множество  ; 2) строим множество
; 2) строим множество  ; 3) строим множество
; 3) строим множество  ; 4) строим множество
; 4) строим множество  ; 5) строим множество
; 5) строим множество  .
. : 1) строим множество
: 1) строим множество  ; 5) строим множество
; 5) строим множество  – формулы, построенные с использованием переменных
– формулы, построенные с использованием переменных  называется тождеством.
называется тождеством.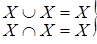 . (1.22)
. (1.22) . (1.23)
. (1.23) . (1.24)
. (1.24) ,
,  ,
,  или в компактном виде, соответственно, записи
или в компактном виде, соответственно, записи  ,
,  ,
,  .
. . (1.25)
. (1.25) . (1.26)
. (1.26) . (1.27)
. (1.27) . (1.28)
. (1.28) . (1.29)
. (1.29) , (*)
, (*) . (**)
. (**) .
. . Тогда
. Тогда  или
или  . Рассмотрим эти случаи:
. Рассмотрим эти случаи: ,
, .
.


