Введение. 1. Основні поняття. Деякі властивості збіжних рядів.
1. Основні поняття. Деякі властивості збіжних рядів. 2. Достатні ознаки збіжності для рядів з додатними членами. 3. Рекомендації щодо використання ознак збіжності рядів з додатними членами. 4. Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінних рядів. 1. Основні поняття. Деякі властивості збіжних рядів Означення. Нехай
називається нескінченним рядом (чи просто рядом), а самі числа Побудуємо частинні суми ряду:
Частинні суми ряду (9.2) утворюють числову послідовність: Означення. Числовий ряд називається збіжним, якщо існує границя послідовності частинних сум ряду
При цьому величина
залишком ряду. Якщо границя Sn не існує (нескінченна), то ряд називається розбіжним. Приклад. Нехай ряд задано першими трьома членами Загальний член ряду, як правило, знаходять методом перебирання варіантів, виходячи із аналізу заданих перших членів ряду з наступною перевіркою його правильності. У даному прикладі чисельник кожного члена дорівнює одиниці, а знаменник є добутком трьох послідовних натуральних чисел. Вважатимемо, що За допомогою методу невизначених коефіцієнтів un можна розкласти на такі дроби:
Часткова сума ряду Sn запишеться тоді так:
У цьому прикладі збіжність ряду було встановлено безпосередньо за означенням, тобто обчислено Теорема 1. Якщо збігається ряд, то збігається його залишок; і навпаки, із збіжності залишку випливає збіжність ряду. Наслідок 1. Із розбіжності ряду випливає розбіжність його залишку, і навпаки. Наслідок 2. Якщо відкинути скінченну кількість перших членів ряду або додати до нього кілька нових членів, то це не вплине на його збіжність. Теорема 2. Якщо члени збіжного ряду (9.1) помножити на сталий множник с, то його збіжність не порушиться, а сума (9.3) помножиться на це число с:
Теорема 3. Збіжні ряди Теорема 4. Послідовність частинних сум збіжного ряду обмежена. Це твердження випливає зі збіжності послідовності частинних сум ряду. Теорема 5. Якщо ряд збігається, то границя його загального члена прямує до 0, тобто: Наслідок. Якщо Приклад: Перевірити виконання необхідної умови збіжності для ряду 2. Достатні ознаки збіжності для рядів з додатними членами Розглянемо ряд Теорема 6 (основна). Для того щоб ряд з додатними членами збігався, необхідно і достатньо, щоб усі його частинні суми були обмеженими. Наслідок. Для того щоб ряд з додатними членами розбігався, необхідно і достатньо, щоб послідовність його частинних сум була необмеженою. Теорема. 7 (ознака порівняння рядів). Якщо для рядів з додатними членами:
виконується умова а) із збіжності ряду (10.7) випливає збіжність ряду (10.6); б) із розбіжності ряду (10.6) випливає розбіжність ряду (10.7). Означення. Якщо для рядів 10.6), (10.7) виконується умова Приклад. Дослідити на збіжність ряд l Загальний член ряду
Ряд порівняння Теорема 8 (ознака порівняння в граничній формі). Якщо для рядів з додатними членами (10.6), (10.7) існує границя Приклад. Дослідити на збіжність ряд l Загальний член ряду
За ознакою порівняння (теорема 9.8) буде розбіжним і ряд
Теорема 9 (ознака Даламбера). Якщо для ряду при при при Приклад. Дослідити на збіжність ряд l Загальний член ряду Теорема 10 (ознака Коші (радикальна)). Якщо для ряду при при при Приклад. Дослідити на збіжність ряд l Загальний член ряду
За ознакою Коші (теорема 9.10) ряд збігається. Теорема 11 (ознака Коші (інтегральна)). Якщо функція Приклад. Дослідити на збіжність ряд Діріхле (узагальнений гармонічний ряд)
l Загальний член ряду
Збіжність інтегралу Діріхле
У частинному випадку при р =1 маємо гармонічний ряд 3. Рекомендації щодо використання ознак збіжності рядів з додатними членами 1. Ознака Даламбера, як правило, дає результати тоді, коли загальний член ряду є відношенням алгебраїчного і трансцендентного виразів або відношенням трансцендентних виразів. Якщо загальний член ряду — алгебраїчний вираз, то ознака Даламбера питання про збіжність не вирішує. 2. Радикальна ознака Коші зручна в тому випадку, коли загальний член ряду містить степенево-показниковий вираз. 3. Інтегральна ознака Коші використовується тоді, коли функція загального члена ряду 4. Ознака порівняння рядів може бути використана для рядів з будь-яким загальним членом. При дослідженні ряду за допомогою ознаки порівняння треба вибрати ряд порівняння, збіжність чи розбіжність якого відома. Рядами порівняння зручно вибирати ряд геометричної прогресії (9.6) або ряд Діріхле (10.8). 5. Якщо загальний член ряду — алгебраїчний вираз, тоді для дослідження збіжності ряду зручно використовувати ознаку порівняння рядів у граничній формі (теорема 3), як це було показано на прикладі. 6. При дослідженні збіжності рядів рекомендується така послідовність дій: 1) встановити тип ряду (знакододатний чи знакозмінний); 2) перевірити виконання необхідної умови збіжності; Приклад. Дослідити збіжність ряду 1) 2) 3) Використаємо достатню ознаку збіжності Даламбера. Побудуємо 4.Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінних рядів Означення. Ряд називається знакозмінним, якщо він містить нескінченне число як додатних, так і від’ємних членів. Теорема 12 (Коші). Якщо збігається ряд із абсолютних величин членів знакозмінного ряду, то збігається і знакозмінний ряд, тобто Означення. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду. Означення. Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається. Зауваження. Якщо знакозмінний ряд збігається абсолютно, то його збіжність зумовлена достатнім спаданням за абсолютною величиною його членів. Зауваження. Якщо знакозмінний ряд збігається умовно, то його збіжність зумовлена не тільки спаданням за абсолютною величиною його членів, але і взаємною компенсацією додатних і від’ємних членів ряду. Приклад. Дослідити на збіжність ряд l Загальний член ряду 5.Знакопочергові ряди. Ознака Лейбніца Означення. Ряд, кожний член якого відрізняється знаком від попереднього, називається знакопочерговим. Цей ряд має вигляд:
Загальний член ряду (10.9) Теорема 13 (Лейбніца). Якщо члени знакопочергового ряду спадають за абсолютною величиною і границя абсолютної величини загального члена ряду дорівнює нулю, то ряд збігається. Коротко цю теорему можна записати так: Наслідок 1. Знак суми збіжного знакопочергового ряду такий само, як і знак першого члена ряду (на рис. 10.1 Геометрична інтерпретація
Рис. 10.1 Наслідок 2. Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує першого члена ряду, тобто Наслідок 3. Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів, тобто Наслідок 4. Якщо для ряду не виконується умова теореми Лейбніца Приклад. Дослідити збіжність ряду Лейбніца
Загальний член ряду 1) 2) Таким чином, ряд Лейбніца буде збіжним, але збіжність умовна, бо ряд із абсолютних величин:
ФИЗИКА методические указания и контрольные работы для студентов заочного отделения.
Череповец, филиал ВоГТУ
Введение Выполнение контрольных заданий по дисциплине «Физика» способствует развитию у студентов навыков практического применения полученных ранее теоретических знаний. Контрольные задания предложены для выполнения двух контрольных работ (Т. И. Трофимова., Сборник задач по курсу физики с решениями: Учеб. пособие для вузов/ Т.И. Трофимова, З.Г. Павлова.- 5-е изд., стер,- М.: Высшая шк., 2004.-591 с.: ил.) В объем контрольных заданий входят семь разделов: 1.ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ; 2.ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ; 3.ЭЛЕКТРИЧЕСКТВО И МАГНЕТИЗМ; 4.КОЛЕБАНИЯ И ВОЛНЫ; 5.ОПТИКА. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ; 6. ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ АТОМОВ, МОЛЕКУЛ И ТВЕРДЫХ ТЕЛ; 7.ЭЛЕМЕНТЫ ФИЗИКИ АТОМНОГО ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ. Контрольная работа №1: разделы 1,2, 3,4,5,6,7– пять задач. Контрольная работа № 2.: разделы 1,2,3,4,5,6,7- пять задач. Номер варианта выбирается по последней цифре шифра. При решении задач необходимо, прежде всего, установить, какие закономерности лежат в основе. Затем, с помощью формул, выражающих эти закономерности, следует найти решение задач в общем виде (т.е. в буквенных обозначениях), причем искомая величина должна быть выражена через заданные величины. После этого можно перейти к подстановке числовых данных, выраженных обязательно в одной и той же системе единиц. При решении задач следует пользоваться единицами измерения физических величин, приведенными в Системе Интернациональной (СИ). Числовой ответ обязательно должен иметь наименование единиц измерения (размерность). При получении числового ответа следует обращать внимание на точность окончательного результата, которая не должна превышать точности исходных величин. Большую часть задач достаточно решить с точностью до двух-трех знаков после запятой. Необходимые для решения задач справочные данные чаще всего указаны в условиях. Если же таковых нет, то необходимо воспользоваться справочной литературой, приведенной в конце методических указаний.
Номера задач для выполнения контрольных заданий № 1,2 по дисциплине «Физика» {Т. И. Трофимова., Сборник задач по курсу физики с решениями: Учеб. пособие для вузов/ Т.И. Трофимова, З.Г. Павлова.- 5-е изд., стер,- М.: Высшая шк., 2004.-591 с.: ил.Ч. Киттель, У. Найт, М. Рудерман Берклеевский курс физики. Т. 1. Механика.- М.: Наука, 1971 }
Список литературы В список литературы включены два известных справочника, учебник Трофимовой и задачник Волькенштейна. Эти издания рекомендуется использовать также в качестве справочных пособий.
1. И. В. Савельев Курс общей физики в 5-ти кн. Кн 1. Механика, М.: Наука, 1998. 2. И. В. Савельев Курс общей физики в 5-ти кн. Кн 3. Молекулярная физика и термодинамика, М.: Наука, 1998. 3. И. В. Савельев Курс общей физики в 3-х т. Т 1. Механика. Молекулярная физика. М.: Наука, 1998. 4. И. Е. Иродов Основные законы механики.-М: Высшая школа, 1985. (и более поздние издания). 5. А. Г. Чертов, А. А. Воробьев Задачник по физике. Изд-е 5-е: М: Высшая школа, 1988. Изд-е 7-е: Физматлит, 2002. Дополнительная: 6. Д. В. Сивухин Общий курс физики в 5-ти т. Т. 1. Механика.- 2002. 7. Д. В. Сивухин Общий курс физики в 5-ти т. Т. 2. Термодинамика и молекулярная физика.- 2002. 8. Т. И. Трофимова Курс физики.- М.: Высшая школа 1990 9. Г. А. Зисман, О. М. Тодес Курс общей физики в 2-х т. Т. 1. Механика. Молекулярная физика. Колебания и волны. 10. С. Э. Фриш, А. В. Тиморева Курс общей физики в 3-х тт. Т. 1. Физматлит, 1962. 11. И. П. Базаров Термодинамика.- М: Высшая школа, 1983. 12. Р. Фейнман, Р. Лейтон, М. Сэндс Фейнмановские лекции по физике. Т.1. Современная наука о природе. Законы механики.- М.: Мир, 1967. Т. И. Трофимова., Сборник задач по курсу физики с решениями: Учеб. пособие для вузов/ Т.И. Трофимова, З.Г. Павлова.- 5-е изд., стер,- М.: Высшая шк., 2004.-591 с.: ил.Ч. Киттель, У. Найт, М. Рудерман Берклеевский курс физики. Т. 1. Механика.- М.: Наука, 1971 14. В. С. Волькенштейн Сборник задач по общему курсу физики- М.: Наука, 1990 15. А. Н. Матвеев Механика и теория относительности.- М.: Высшая школа, 1985. 16. М. Борн Эйнштейновская теория относительности.- М.: МИР, 1964. 17. И. Е. Иродов Задачи по общей физике.- М.: 1997
|

 — деяка нескінченна послідовність чисел. Побудований із цих чисел за допомогою знака «+» символ
— деяка нескінченна послідовність чисел. Побудований із цих чисел за допомогою знака «+» символ (10.1)
(10.1) — членами ряду; n -ий член un — називається загальним членом ряду.
— членами ряду; n -ий член un — називається загальним членом ряду.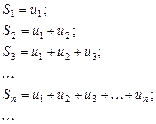 (10.2)
(10.2) Надалі основним буде питання про збіжність послідовності частинних сум ряду. Таким чином, поняття ряду вводиться для побудови числових послідовностей спеціального виду — частинних сум ряду. Такі послідовності широко використовуються в математичному аналізі, наприклад, відоме число е можна подати таким рядом
Надалі основним буде питання про збіжність послідовності частинних сум ряду. Таким чином, поняття ряду вводиться для побудови числових послідовностей спеціального виду — частинних сум ряду. Такі послідовності широко використовуються в математичному аналізі, наприклад, відоме число е можна подати таким рядом  .
. (10.3)
(10.3) називається сумою ряду, а число
називається сумою ряду, а число — (10.4)
— (10.4)
 . Знайти загальний член ряду і дослідити ряд на збіжність.
. Знайти загальний член ряду і дослідити ряд на збіжність. . Тоді, беручи n послідовно таким, що дорівнює 1, 2, 3,..., дістаємо члени ряду
. Тоді, беручи n послідовно таким, що дорівнює 1, 2, 3,..., дістаємо члени ряду  ;
;  , чим упевнюємося, що загальний член ряду
, чим упевнюємося, що загальний член ряду  побудований правильно.
побудований правильно. .
.
 . Отже, ряд збігається, його сума
. Отже, ряд збігається, його сума  .
. . Для переважної більшості рядів обчислити
. Для переважної більшості рядів обчислити 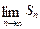 неможливо, тому далі буде наведено такі методи й ознаки, за допомогою яких можна встановити збіжність ряду, не обчислюючи
неможливо, тому далі буде наведено такі методи й ознаки, за допомогою яких можна встановити збіжність ряду, не обчислюючи  .
. і
і  можна почленно додавати або віднімати, при цьому ряд
можна почленно додавати або віднімати, при цьому ряд 
 також збігається, а його сума буде
також збігається, а його сума буде  .
. .
. , тобто необхідна умова збіжності ряду не виконується, то ряд розбігається.
, тобто необхідна умова збіжності ряду не виконується, то ряд розбігається. . Загальний член ряду
. Загальний член ряду  . Розглянемо
. Розглянемо 
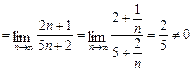 . Необхідна умова збіжності ряду не виконується. Ряд розбігається.
. Необхідна умова збіжності ряду не виконується. Ряд розбігається. з додатними членами
з додатними членами 
 . Частинні суми ряду (9.2) утворюють при цьому монотонно зростаючу послідовність
. Частинні суми ряду (9.2) утворюють при цьому монотонно зростаючу послідовність  .
.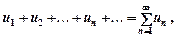 (10.6)
(10.6) (10.7)
(10.7)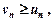 то:
то: , то ряд (10.7) називається мажорантним відносно ряду (10.6), а ряд (10.6) — мінорантним відносно ряду (10.7).
, то ряд (10.7) називається мажорантним відносно ряду (10.6), а ряд (10.6) — мінорантним відносно ряду (10.7). .
. . Зауважимо, що
. Зауважимо, що .
. збігається як ряд геометричної прогресії із
збігається як ряд геометричної прогресії із  . Значить, за ознакою порівняння (теорема 10.7) ряд
. Значить, за ознакою порівняння (теорема 10.7) ряд 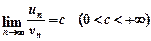 , то ряди (10.6) і (10.7) збігаються або розбігаються разом.
, то ряди (10.6) і (10.7) збігаються або розбігаються разом. .
. являє собою алгебраїчний вираз. Для того щоб цілеспрямовано вибрати ряд порівняння, побудуємо величину, еквівалентну
являє собою алгебраїчний вираз. Для того щоб цілеспрямовано вибрати ряд порівняння, побудуємо величину, еквівалентну  при
при 
 . Вибираємо ряд порівняння
. Вибираємо ряд порівняння  — гармонічний ряд, він є розбіжним. Обчислюємо
— гармонічний ряд, він є розбіжним. Обчислюємо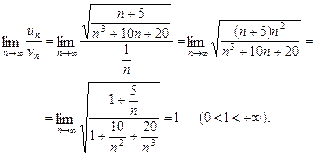
 з додатними членами
з додатними членами  існує границя
існує границя  тоді:
тоді: ряд збігається;
ряд збігається; ряд розбігається;
ряд розбігається; питання про збіжність ряду ознака не вирішує.
питання про збіжність ряду ознака не вирішує.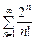 .
. . Побудуємо
. Побудуємо 
 і розглянемо
і розглянемо  . За ознакою Даламбера ряд
. За ознакою Даламбера ряд  з додатними членами
з додатними членами  існує границя
існує границя  , тоді:
, тоді: ряд збігається;
ряд збігається;
 .
.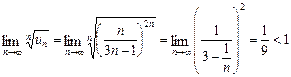 .
. неперервна, додатна і монотонно спадає при
неперервна, додатна і монотонно спадає при 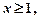 то ряд
то ряд  і невластивий інтеграл
і невластивий інтеграл  збігаються або розбігаються разом.
збігаються або розбігаються разом. (10.8)
(10.8) . Побудуємо функцію
. Побудуємо функцію  :
: .
. встановлено в 7.3.1, таким чином, за теоремою 10.11
встановлено в 7.3.1, таким чином, за теоремою 10.11 .
.
 який, як тепер встановлено, буде розбіжним.
який, як тепер встановлено, буде розбіжним. легко інтегрується.
легко інтегрується. .
. ряд знакододатний.
ряд знакододатний.
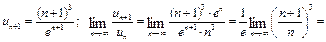
 ряд
ряд 
 .
. залежно від n може бути як додатним, так і від’ємним. Отже, ряд
залежно від n може бути як додатним, так і від’ємним. Отже, ряд  . Цей ряд буде знакододатним
. Цей ряд буде знакододатним  , так що для дослідження його на збіжність можна використати ознаки збіжності знакододатних рядів. Скористаємось ознакою порівняння рядів:
, так що для дослідження його на збіжність можна використати ознаки збіжності знакододатних рядів. Скористаємось ознакою порівняння рядів:  — ряд порівняння, він збігається, як ряд Діріхле, з p = 2 > 1. Отже, за ознакою порівняння (теорема 10.7) ряд
— ряд порівняння, він збігається, як ряд Діріхле, з p = 2 > 1. Отже, за ознакою порівняння (теорема 10.7) ряд 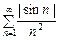 збігається, а це означає, що за теоремою Коші збігається і ряд
збігається, а це означає, що за теоремою Коші збігається і ряд  , причому збігається абсолютно.
, причому збігається абсолютно. (10.9)
(10.9) де
де  .
.
 ).
).
 (на рис. 9.1) 0< S < a 1).
(на рис. 9.1) 0< S < a 1). .
. , то ряд розбігається (не виконується необхідна умова збіжності).
, то ряд розбігається (не виконується необхідна умова збіжності).
 почергово змінює знак, отже, ряд Лейбніца — знакопочерговий. Обидві умови теореми Лейбніца для цього ряду виконуються:
почергово змінює знак, отже, ряд Лейбніца — знакопочерговий. Обидві умови теореми Лейбніца для цього ряду виконуються: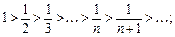
 .
.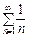 — гармонічний ряд, що розбігається.
— гармонічний ряд, що розбігається.


