Итоговые контрольные задания № 2
К каждому заданию дано несколько ответов. Укажите верный ответ, сопроводив задание кратким решением.
1. Упростите выражение: а. б. в. г.
2. Решите уравнение: а. б. в. г.
3. Найдите производную функции а. б. в. г.
4. а. б. в. г.
5. Решите неравенство а. б. в. г.
6. Найдите промежутки убывания функции а. б. в. г.
7. Найдите диагональ правильной четырехугольной призмы, если сторона основания а. б. в. г.
8. Найдите объем конуса, полученного в результате вращения прямоугольного треугольника с гипотенузой а. б. в. г.
9. Из данных выражений выберите то, которое имеет смысл. а. б. в. г.
10. Укажите, график какой функции схематично изображен на рисунке. а. б. в. г.
11. Найдите функцию, для которой функция а. б. в. г.
12. Решите уравнение а. б. в. г.
Приложение 1 Разноуровневые задания по алгебре1 Для закрепления основных умений и выработке навыков. Предлагаемые задания могут быть использованы как в качестве дополнительных упражнений на занятиях, так и для самостоятельной работы, в частности, при подготовке к контрольным работам. Как правило, выделяются три уровня возрастающей сложности от 1 к 3. Арифметические преобразования Вычислите: 1. а) б) в) г) д) е) ж) з) и) к) л) м)
1 Могут использоваться также преподавателями для составления индивидуальных заданий-карточек с целью дифференциации обучения.
2. а) б) в)
г) д) е) ж) з) и) к)
3. а) б) в) г)
Дробно-рациональные неравенства Решите неравенства: 1. а) б) в) г) д) е) ж) з) и) к) л) м) н)
2. а) б) в) г) д) е) ж) 3. а) б) в) г) д) е) ж)
Уравнения и неравенства с модулем Решите уравнения и неравенства: 1. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) 2. а) б) в) г) д) е) ж) з) и) к) л) м) н) о)
п) р) с) т) у) ф) Определение и свойства тригонометрических функций Вычислите: 1. а)sinα и tgα, если cosα= б)cosα и tgα, если sinα=0,6 и в)sinα и tgα, если cosα= г)sinα и tgα, если cosα=- д)cos2α, если tgα= е)3tg2α, если tgα=0,5; ж)cosα, если tg з)sin2 и)sin к) л) м) н) о) 2. а) б) в) г) д) е) ж)
3. а) б) в) г) д) е) ж) з) и)
Тригонометрические уравнения Решите уравнения: 1. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) 2. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) у) ф)
3. а) б) в) г) д) е) ж) з) и) к) л) м)
Иррациональные уравнения и неравенства Решите уравнения и неравенства: 1. а) б) в) г) д) е) ж) з) и) к) 2. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) у)
3. а) б) в) г) д) е) ж) з) и) к) л)
Показательные уравнения и неравенства Решите уравнения и неравенства: 1. а) б) в) г)
д) е) ж) з) и) к) л) м) 2. а) б) в) г) д) е) ж) з) и) к) 3. а) б) в) г) д) е) ж)
Определение и свойства логарифма Вычислите: 1. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с)
2. а) б) в) г) д) е) ж) з) и)
3. а) б) в) г) д) е) ж) з) Логарифмические уравнения и неравенства Решите уравнения и неравенства: 1. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) у) ф)
2. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р) 3. а) б) в) г) д) е) ж) з)
|

 .
. ;
; ;
; ;
; .
. .
. ;
; ;
; ;
; .
. .
. ;
; ;
; ;
; .
. Ребро куба
Ребро куба  равно 4. Найдите расстояние от вершины
равно 4. Найдите расстояние от вершины  до прямой
до прямой  .
. ;
; ;
; ;
; .
. .
. ;
; ;
; ;
; .
. .
. ;
; ;
; ;
; .
. , высота
, высота  .
. ;
; ;
; .
. и острым углом
и острым углом  вокруг меньшего катета.
вокруг меньшего катета. ;
; ;
; ;
; .
. ;
; ;
; ;
; .
.
 ;
; ;
; ;
; .
. является первообразной.
является первообразной. ;
;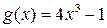 ;
; ;
; .
. .
. ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;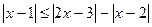 ;
; ;
; ;
; ;
; ;
; .
. и 0<α<π;
и 0<α<π; ;
; и
и  ;
; и
и  ;
; ;
; ;
; -cos2
-cos2  cos
cos  ;
; ;
;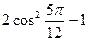 ;
; ;
; ;
; .
. , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; ;
; ;
; .
. ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  ;
; , если
, если  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;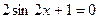 ;
; ;
; .
.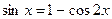 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;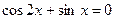 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;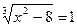 ;
; .
. ;
;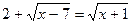 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;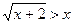 ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;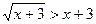 ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.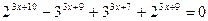 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
;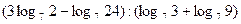 ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; ;
;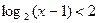 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;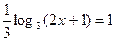 ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;



