ТЕСТОВЫЕ ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ
а) это синоним подсудности в том смысле, что обвиняемый в ходе процесса должен отвечать на вопросы судьи о каких-либо своих действиях или их последствиях; б) это необходимость расплачиваться за предвидимые последствия своих действий; в) это синоним добросовестного исполнения профессионального долга; г) всё перечисленное. 12. Ответственность становится нормативным требованием к современной инженерной компетентности: а) в связи с появлением информационно-коммуникационных способов воздействия на сознание; б) в связи с появлением ядерной энергетики; в) в связи с появлением других современных глобальных технологий; г) все вышеперечисленное.
13. В современном мире применительно к инженерной деятельности под ответственностью понимают: а) синонимом подсудности; б) необходимость отвечать за предвидимые последствия своих действий; в) добросовестное исполнение профессионального долга; г) все вышеперечисленное. 14. Оценка техники представляет собой: а) особую модель разделения и делегирования ответственности за предупреждения отдалённых и непредвидимых последствий технической деятельности; б) экономический анализ эффективности внедрения той или иной технической новинки; в) научную поддержку политических решений применительно к техническому развитию; г) все вышеперечисленное. 15. К системному кризису инженерии, выражающемуся, в осознании отрицательных последствий инженерной деятельности привело: а) разрушение и изменение природы (экологический кризис); б) неконтролируемые изменения второй и третьей природы: деятельности, организаций, социальных инфраструктур (кризис развития); в) изменение и разрушение человека (антропологический кризис); г) всё перечисленное. 16. Под оценкой техники можно понимать: а) механизм реализации индивидуальной или групповой ответственности; б) делегирование части социальной ответственности; в) некий социокультурный институт, обеспечивающий социальную коммуникацию, включенность в который представляется элементом социокультурной компетентности; г) специальные рекомендации относительно предписания ответственности субъектам технической деятельности.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ТЕСТОВЫЕ ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ $$$ 1. Вычислить
A) –1; B) 0; C) 1; D) 2; E) 3.
$$$ 2. Вычислить:
A) B) C) D) 2; E) –2.
$$$ 3.
A) –11; B) –10; C) –9; D) –6; E) –3.
$$$ 4.
A) B) C) D) E) E)
$$$ 5. Какому из пределов равна частная производная по у от функции z = f(x,y)?
A) B) C) D) E)
$$$ 6. Дана функция z(x,y) = 4x – 4y – x2 – y2. Найти стационарную точку.
A) (2,–2) B)(1, 2) C) (–2, 0) D) (–2, 2) E) (0, 2)
$$$ 7. Дана функция z = ln (x + y2). Вычислить A) B) C) D) E)
$$$ 8. Найдите определение неопределенного интеграла.
A) B) D) C) E)
$$$ 9. Какое условие должно выполняться для a в табличном интеграле
A) a ¹ 1 B) a ¹ –1 C) a ¹ 0 D) a > 0 E) a< 0
$$$ 10. Чему равен интеграл
A) 5 cos(–5x) + C B) – C). D). E)
$$$ 11. Сколько раз применяется интегрирование по частям при нахождении интеграла
A) 1 B) не применяется C) 5 D) 3 E) 2
$$$ 12. Каков геометрический смысл определенного интеграла
A) Длина дуги кривой y =f(x) между прямыми х=а и х=b. B) Длина отрезка [a,b]. C) Площадь криволинейной трапеции, ограниченной кривой y =f(x), осью Ох и прямыми x=a, x=b. D) Площадь криволинейной трапеции, ограниченной осями Ох и Оу, кривой y=f(x) и прямой x=b. E) Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной кривой y=f(x), прямыми x=а и х=b.
$$$ 13. Вычислите интеграл A) B) C) D) E) 0
$$$ 14. Найти площадь фигуры, ограниченной параболой y=4–x2 и осью Ох, с помощью определенного интеграла
A) B) C). D) E)
$$$ 15. Найти необходимый признак сходимости ряда A) B) C) D) E)
$$$ 16. Что называется порядком дифференциального уравнения?
A) наибольшая степень переменной х B) наибольшая степень у(х) C) порядок старшей производной D) порядок наименьшей производной E) наименьшая степень у(х)
$$$ 17. Решить дифференциальное уравнение xdx + ydy = 0.
A) 2x + 2y = C B) x + y2 + C = 0 C) x2 + 2y – C = 0 D) E) x2 – y2 = C
$$$ 18. Найти предел: A) B) 0 C) D) 5 E) ПОН
$$$ 19. Найти предел: A) B) 0 C) D) E) ПОН
$$$ 20. Найти производную функции A) B) C) D) E)
$$$ 21. Дана функция A) B) C) 1 D) 4 E)
$$$ 22. Дано уравнение y” + 4y = 0. Найти корни его характеристического уравнения.
A) k1 = 2i, k2 = –2i B) k1 = 2, k2 = –2 C) k1 = k2 = 2 D) k1 = k2 = 2i E) k1 = 4, k2 = 0
$$$ 23. Проинтегрировать следующее дифференциальное уравнение (1 + y2)dx + (1 + x2)dy = 0.
A) (1 + y2)(1 + x2) = C B) arctgx + arctgy + C C) ln(1 + y2)(1 + x2) = C D) 1 + y = x + C E)
$$$ 24. Вычислить A) B) C) 1; D) 4; E) 0.
$$$ 25. Вычислить: A) B) 0; C) D) –3; E) 1.
$$$ 26.
A) –11; B) –13; C) 5; D) 4; E) –9.
$$$ 27.
A) B) C) D) E)
$$$ 28. Полное приращение функции
A) Dz = (x + Dx)y – xy B) Dz = (x + Dx)(y + D y) – (x + Dx)y C) Dz = (x, y + Dy) – (x + Dx, y) D) Dz = (x + Dx)(y + D y) – xy E) Dz = (x + Dx + D y) xy.
$$$ 29. Дана функция z = 4x3 – 3x2y – 3xy + y. Найти A) 10 B) 6 C) 12 D) 0 E)–12
$$$ 30. Найти полный дифференциал функции A) B) C) D) xdx + ydy; E)
$$$ 31. Первообразной для функции f(x) = х3 будет функция
A) F(x) = 3х2; B) F(x) = 4х3; C) D) F(x) = 4x5; E) $$$ 32.
A) B) C) D) E)
$$$ 33.
A) arctg 3x + C; B) C) ln|x2+9| + C; D) E)
$$$ 34. Интеграл
A) B) C) D) E) –
$$$ 35. Укажите формулу интегрирования по частям A) B) C) D) E)
$$$ 36. Чему равен интеграл A) 4 B) 2. 1 C) 3 D) 0 E) e
$$$ 37. Указать формулу для вычисления площади заштрихованной фигуры
y=x2
0 x
x=y2 A) B) C) D) E)
$$$ 38. Дан ряд A) B) C) 1 D) E) 5.
$$$ 39. Общим решением дифференциального уравнения F(x, y(x), y’(x), y”(x)) = 0 является A) любая функция у = j(х), удовлетворяющая этому уравнению B) кривая, проходящая через заданную точку М0(х0, у0) C) функция, содержащая производную постоянную С D) функция у = j(х, С1, С2,…,Сn), удовлетворяющая этому уравнению E) функция, содержащая две независимые произвольные постоянные С1 и С2
$$$ 40. Найти общее решение уравнения A) y = 5x2 + C; B) y = 5x + C; C) D) E)
$$$ 41. По характеристическому уравнению 3k 2 + 5k = 0 написать искомое дифференциальное уравнение.
A) 3y’ + 5y = 0; B) 3y” + 5 = 0; C) 3y + 5 = 0; D) 3y’ + 5 = 0; E) 3y” + 5y’ = 0.
$$$ 42. Найти общее решение уравнения A) y = x2 + C; B) y = x + C; C) D) E)
$$$ 43. Вычислить A) 1; B) C) D) E)
$$$ 44. Вычислить: A) –2,5; B) –1; C) D) 2,5; E) 5.
$$$ 45.
A) 6; B) 4; C) 3; D) 2; E) 0.
$$$ 46.
A) –11; B) 13; C) 1; D) –1; E)
$$$ 47. Найти формулу полного дифференциала функции z = f(x,y). A) B) C) D) E)
$$$ 48. Найти предел: A) B) 0 C) D) 6 E) ПОН
$$$ 49. Найти предел: A) 0 B) C) D) E) ПОН
$$$ 50. Найти производную функции A) B) C) D) E)
$$$ 51. Дана функция z = xy – siny. Найти A) 1 – cos y; B) x – cos y; C) – cos y; D) cos y; E) sin y.
$$$ 52. Найти стационарную точку функции z = x2 + xy + y2 + x – y + 1. A) (1, 2); B) (0, 1); C) (1, 0); D) (–1, 1); E) (1, 1).
$$$ 53. Первообразная для функции f(x) есть A) B) C) D) E)
$$$ 54.
A) 5tg x + C; B) C) –5sin2x + C; D) ctg x + C; E) –5cos2x + C.
$$$ 55. Укажите верное значение интеграла A) B) C) D) E)
$$$ 56. Укажите интеграл, к решению которого применяется метод замены переменной. A) B) C) D) E)
$$$ 57. Укажите верное равенство. A) B) C) D) E)
$$$ 58. Вычислите интеграл A) ln 3; B) ln 2; C) ln (4–e); D) ln (2+e); E) 2.
$$$ 59. Найти площадь фигуры, образованной осями Ох, Оу и прямой х+у–4=0
A) 16 B) 2 C) 10 D) 4 E) 8
$$$ 60. Дан гармонический ряд A) B) 1 C) D) E)
$$$ 61. Дифференциальное уравнение M(x,y)dx + N(x,y)dy = 0 называется однородным, если A) М(х, у), N(x,y) – произвольные функции B) M(x,y) = m(x)n(y), N(x,y) = m1(x)n1(y) C) D) М(х, у), N(x,y) – однородные функции одного и того же порядка E) М(х, у), N(x,y) – непрерывные функции
$$$ 62. Дифференциальное уравнение A) y = 3 sinx + C; B) C) y = sinx; D) y = 3 sinx; E)
$$$ 63. Укажите корни характеристического уравнения для дифференциального уравнения A) k1 = 4, k2 = 1; B) k1 = 4, k2 = 4; C) k1 = –4, k2 = 1; D) k1 = 4, k2 = –1; 5)k1 = 0, k2 = 2.
$$$ 64. Найти общее решение уравнения y2dx – x2dy = 0 A) B) y = C – 2x; C) 2x2y = C; D) y2 + x2 = C; E)
$$$ 65. Вычислить A) –5; B) 0; C) 1; D) 3,5; E) 7.
$$$ 66. Вычислить: A) –3; B) C) 3; D) 0; E)
$$$ 67.
A) 5; B) 6; C) 7; D) 8; E) 9.
$$$ 68.
A) –0,5; B) 0,5; C) 0,28; D) 0,2; E) –0,2.
$$$ 69. Дана функция z = f(x,y). Как называется выражение вида Dz = f(x + Dx, y + Dy) – f(x,y)?
A) частное приращение по х; B) полное приращение; C) частная производная по у; D) смешанная производная; E) полный дифференциал.
$$$ 70. Найти A) 3y2x; B) 6xy; C) 6y3x; D) 6xy2; E)2xy3.
$$$ 71. Найти частную производную
A) 12х + 6ху; B) 12х + 6у; C) 12ху; D) 12х2у; E) 6х2у + 5.
$$$ 72. Чему равно
A) f(x); B) f(x)dx; C) F(x) + C; D) F(x)dx; E) f’(x).
$$$ 73.
A) ln|2x–3| + C; B) C) D) ln(2x–3)2 + C; E)
$$$ 74. Как называется функция вида
A) рациональная B) иррациональная C) степенная D) показательная E) степенной ряд.
$$$ 75. Чему равен интеграл
A) –cos x; B) 1; C) sin x + C; D) cos x + C; E) sin x.
$$$ 76. Вычислите интеграл A) 16 B) 8 C) 4 D) 0 E) ¥
$$$ 77. Чему равен интеграл A) 5 B). 52 C) 10 D 0 E) 1
$$$ 78. Найти предел:
A) 0 B) C) D) E) ПОН
$$$ 79. Найти предел:
A) 3 B) 0 C) 1 D) E) ПОН
$$$ 80. Найти производную функции
A) B) C) D) E)
$$$ 81. Дана функция
A) 5,5 B) 6,5 C) 11,5 D) E)
$$$ 82. Чему равна площадь заштрихованной фигуры?
y =sin x
0 p/2 p x
A) 2 B) 1 C) D) p E) 0
$$$ 83. Для какого из рядов выполняется необходимое условие сходимости? A) B) C) D) E)
$$$ 84. Процесс нахождения решения дифференциального уравнения называется
A) логарифмированием B) дифференцированием C) преобразованием D) заменой переменной E) интегрированием.
$$$ 85. Написать характеристическое уравнение для дифференциального уравнения A) B) 5k2 + 4k = 0; C) 5k2 – 4k = 0; D) 5k2 + 4 = 0; E) 5k2 – 4 = 0.
$$$ 86. Написать дифференциальное уравнение, характеристическое уравнение которого записывается в виде к2 – 2к – 5 = 0.
A) y” – 5y – 2 = 0; B) y’ – 2y – 5 = 0; C) y” – 2y’ – 5 = 0; D) y” – 2y’ – 5y = 0; E)y” – 5y’ – 2 = 0.
$$$ 87. Дано уравнение с разделяющимися переменными xy’ – y = 0. Решить его. A) y = Cx; B) C) x – y = C; D) y = ex + C; E)y = Cx2.
$$$ 88. Вычислить A) B) C) –2; D) –1,5; E)
$$$ 89. Вычислить: A) B) 1; C) 2; D) E) 0.
$$$ 90.
A) –1; B) 1; C) D) E)
$$$ 91.
A) B) 0,5; C) –0,5; D) 0,2; E) –0,2.
$$$ 92. Укажите формулу для нахождения частного приращения A) Dxz = f(x +Dx, y + Dy) – f(x,y); B) Dxz = f(x +Dx, y) – f(Dx,y); C) Dxz = f(x, y) – f(Dx,y); D) Dxz = f(x +Dx, y + Dy) – f(x + Dx,y); E) Dxz = f(x +Dx, y) – f(x,y).
$$$ 93. Найти необходимые условия экстремума функции двух переменных.
A) B) C) D) E)
$$$ 94. Пусть М0(х0, у0) – стационарная точка функции z = f(x,y). Обозначим A) D < 0, А > 0; B) D > 0, В > 0; C) D = 0, А > 0; D) D > 0, А > 0; E) D < 0, А > 0.
$$$ 95.
A) arctg 3x + C; B) C) ln|x2+9| + C; D) E)
$$$ 96. Найти интеграл A) B) C) D) E)
$$$ 97. При решении интеграла применяется A) замена переменной B) интегрирование тригонометрических функций C) интегрирование рациональных функций D) интегрирование по частям C) интегрирование иррациональных функций
$$$ 98. Для нахождения интеграла A) B) C) D) E)
$$$ 99. Укажите формулу Ньютона–Лейбница.
A) B) C) D) C)
$$$ 100. Для любых трех чисел a, b, c, удовлетворяющих условию a<c <b, справедливо равенство:
A) B) C) D) E)
$$$ 101. Укажите точки разрыва подынтегральной функции в определенном интеграле A) х =2; B) х = 1, х = 5; C) х = 2, х = 0; D) х = 4; C) х = 0, х = 4.
$$$ 102. По виду общего члена A) B) C) D) E)
$$$ 103.
Общим интегралом уравнения y’ = f(x,y) называется решение, записанное в виде
A) у = Сх; B) у = j(х, С); C) у = С + х; D) Ф(х, у, С) = 0; E) х = j(у, С).
$$$ 104. Каков порядок дифференциального уравнения F(x, y, y’, y”, y(IV)) = 0?
A) 4 B) 3 C) 1 D) 0 E) 2
$$$ 105. Линейное дифференциальное уравнение 1–го порядка имеет вид A) B) C) D) E)
$$$ 106. Найти характеристическое уравнение для уравнения A) B) k2 + 2 = 0; C) k2 – 3k + 2 = 0; D) k2 – 3k = 0; E) k – 3k + 2 = 0.
$$$ 107. Найдите производную функции A) B) C) D) E)
$$$ 108. Найдите производную функции A) B) C) D) E)
$$$ 109. Найти предел
A) B) 2 C) D) E) 0
$$$ 110. Найти предел
A) B) 2 C) D) E) ¥
$$$ 111. .Найти производную функции
A) B) C) D) E) 12 х + 4
$$$ 112. Дана функция
A) B) C) D) E) 0
$$$ 113. Найдите производную функции y = 14 A) B) C)
D) E)
$$$ 114. Найдите производную функции y = 6 A) B) C) D) E) 4
$$$ 115. Найдите производную функции y = 6
A) B) C) D)
|

 .
. .
. ;
; ;
; ;
; . Вычислить
. Вычислить  .
.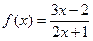 . Вычислить
. Вычислить  .
. ;
; ;
;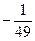 ;
; ;
; .
.





 в точке М0(–1,3).
в точке М0(–1,3).




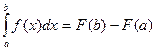





 ?
?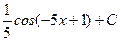


 ?
? ?
? .
.

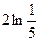



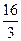










 .
.




 , вычислить
, вычислить  .
.

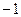

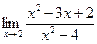 .
. ;
; ;
; .
. ;
; . Вычислить
. Вычислить 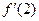 .
. ;
; ;
; ;
; вычисляется по формуле
вычисляется по формуле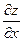 в точке М0 (0,–2).
в точке М0 (0,–2).
 ;
; ;
; ;
; .
. ;
; .
. равен
равен ;
; ;
; ;
; ;
; .
. равен
равен ;
; ;
; .
. равен
равен ;
; ;
; ;
;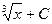 ;
;



 .
. ?
?

 y
y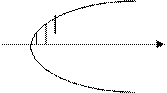
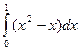 ;
; ;
; ;
; ;
;
 Найти S3 – S2.
Найти S3 – S2.


 .
.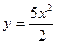 ;
; ;
; .
. .
. ;
; ;
; .
.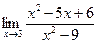 .
.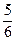 ;
; ;
; .
.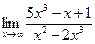 .
. . Вычислить
. Вычислить  . Вычислить
. Вычислить 








 .
. ;
;



 .
. . Чему равна функция f(x)?
. Чему равна функция f(x)? ;
; ;
; ;
; ;
; .
. равен
равен ;
;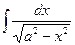 .
. ;
; ;
;
 ;
; .
. ;
; ;
; ;
; ;
; .
.
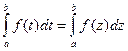


 .
.
 . Найти сумму S1 + S2 частичных сумм S1 и S2.
. Найти сумму S1 + S2 частичных сумм S1 и S2.


 имеет общее решение вида
имеет общее решение вида ;
; .
.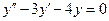 .
. ;
; .
. .
.
 . Вычислить
. Вычислить  . Вычислить
. Вычислить  .
. для функции z = x2y3.
для функции z = x2y3. для функции z = 2х3 + 3х2у2 + 5у – 3.
для функции z = 2х3 + 3х2у2 + 5у – 3. ¢?
¢? равен
равен ;
; ;
; .
. ?
? ?
? .
. ?
?




 .
.




 , вычислить
, вычислить  .
.

 y
y

 ;
; ;
; ;
;
 .
. .
. ;
; ;
; .
. ;
; ;
; .
. .
. . Вычислить
. Вычислить  .
. .
. . Вычислить
. Вычислить  ;
; функции
функции 
 ;
;
 ;
; ;
; ;
;
 .
. ,
,  ,
,  и D = АС – В2. Тогда в точке М0 функция имеет минимум, если в этой точке:
и D = АС – В2. Тогда в точке М0 функция имеет минимум, если в этой точке: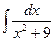 равен
равен ;
; ;
; .
. .
. ;
; ;
; ;
; ;
;
 подынтегральную функцию разлагаем на дроби
подынтегральную функцию разлагаем на дроби  . Найти неопределенные коэффициенты.
. Найти неопределенные коэффициенты.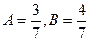 ;
; ;
; ;
; ;
; .
.
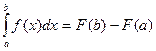

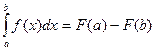
 .
.



 .
. .
. найти искомый ряд.
найти искомый ряд. ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
; .
. .
. ;
;
 ;
; ;
; ;
; ;
; .
.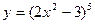
 ;
; ;
; ;
; ;
; .
.



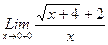



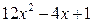

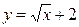 найти
найти 



 .
. ;
; ;
; ;
; ;
; .
.