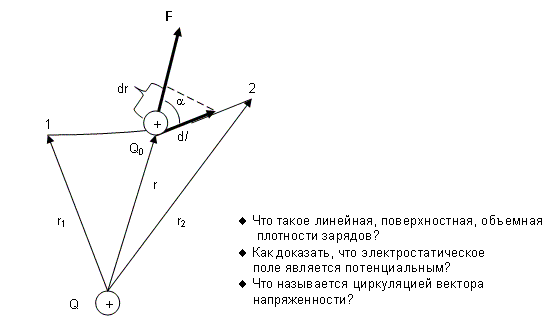
Электростатического поля. Если в электростатическом поле точечного заряда Qиз точки 1 в точку 2вдоль произвольное траектории (рис
Если в электростатическом поле точечного заряда Qиз точки 1 в точку 2вдоль произвольное траектории (рис. 132) перемещается другой точечный заряд Q0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении d l равна
Рис. 132
Так как d/cosa = dr, то
Работа при перемещении заряда Q0 из точки 1в точку 2
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными (см. § 12). Из формулы (83.1) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работ а сил поля на пути dl равна Edl = E l d l, где E l = Ecosa - проекция вектора Е на направление элементарного перемещения. Тогда формулу (83.2) можно записать в виде
Интеграл Формула (83.3) справедлива только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов условие (83.3) не выполняется (для него циркуляция вектора напряженности отлична от нуля).
|



 (83.1)
(83.1) . (83.2)
. (83.2)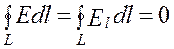 (83.3)
(83.3) называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.


