Средние значения
Необходимо знать виды средних величин и технику их вычисления (средняя арифметическая, средняя арифметическая взвешенная, средняя геометрическая, среднее квадратическое отклонение, мода, медиана, коэффициент вариации). Средняя величина - это обобщающий показатель, который характеризует качественно однородную совокупность по определенному количественному признаку. Например, средний возраст лиц, осужденных за кражу. Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи, с чем каждый вариант приходится умножать на соответствующую численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту называют статистическим весом. Средняя арифметическая простая – самый распространенный вид средней. Она равна сумме отдельных значений признака, деленной на общее число этих значений:
где x1,x2, …,xN – индивидуальные значения варьирующего признака (варианты), а N – число единиц совокупности. Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов:
где xi – значение i–й варианты признака; fi – частота i–й варианты. Таким образом, каждое значение варианты взвешивается по своей частоте, поэтому частоты иногда называют статистическими весами. Замечание. Если вычисление средней величины производят по данным, сгруппированным в виде интервальных рядов распределения, то сначала надо определить серединные значения каждого интервала х'i, после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, где вместо xi используется х'i. Вариация – это различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Показатели вариации используются для установления типичности средней величины, т. е. насколько точно характеризует средняя данную совокупность по определенному признаку. К основным показателям вариации относятся следующие: 1) Дисперсия дисперсия; 2) среднее квадратическое отклонение; коэффициент вариации определяется как средняя из отклонений, возведенных в квадрат. Простая дисперсия для не сгруппированных данных:
Взвешенная дисперсия для вариационного ряда:
Замечание. На практике для вычисления дисперсии лучше использовать следующие формулы: Для простой дисперсии
Для взвешенной дисперсии Среднее квадратическое отклонение - это корень квадратный из дисперсии:
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем, однороднее совокупность и тем лучше средняя арифметическая отражает собой всю совокупность. Коэффициент вариации – выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
Коэффициент вариации используют не только для сравнительной оценки вариации разных признаков или одного и того же признака в различных совокупностях, но и для характеристики однородности совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному распределению). Необходимо также хорошо усвоить графический метод представления статистических данных. Познакомиться с видами графиков, типами диаграмм и примерами их использования для анализа судебнойстатистики (точечные, линейные, столбиковые, полосковые, секторные).
|

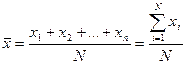 ,
,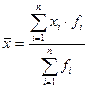 ,
, .
.
 .
.





