Э Л Е К Т Р О М А Г Н И Т Н Ы Е Я В Л Е Н И Я 7 страница
Угол дает разность фаз между напряжением U и силой тока I. По векторной диаграмме (см. также выражение (7.7)) находим:
где
Таким образом, резонансная частота для тока в контуре не зависит от активного сопротивления R и совпадает с собственной частотой контура:
Так как UR и ток в цепи изменяется синфазно, то ясно, что амплитуда URm будет максимальной при ω = ωр. При этом URm = Um. Для Ucm и ULm с учетом выражений (7.5) и (7.10) имеем:
При
Величину называют добротностью контура. Таким образом, добротность контура показывает, во сколько раз амплитуда Ucm и ULm превышает амплитуду Um, приложенного к цепи напряжения при ω=ωp. На рис. 7.3.б показана зависимость Ucm от частоты ω при разных R, максимальные амплитуды Ucm и ULm (Um считаем постоянной) и со- ответствующие резонансные частоты ωcр и ωcL найдем, дифференцируя по w выражения для Ucm и ULm (7.12) и решая уравнения
В результате получим следующие значения для резонансных частот:
На рис.7.4 показана зависимость URm, ULm и UCm от частоты w. При w = wр URm = Um, а ULm = UCm = QUm. UCm имеет максимум при wcр<wр, а ULm при wLр>wр.
(Im/Imрез)2 = 0,5 при (ωL - 1/ωC)2 = R2. Это уравнение имеет два корня w1 и w2 (см.рис.7.3.а). Проведя необходимые выкладки, можно убедиться, что при больших добротностях
Соотношение (7.18) дает возможность экспериментального определения добротности Q по резонансной кривой силы тока в контуре.
7.2. Описание установки
Принципиальная схема установки показана на рис.7.5. Для возбуждения колебаний в контуре, образованном сопротивлением R, емкостью С и индуктивностью L (величины даны на установке), со звукового генератора (ЗГ) подается переменное напряжение.
значения тока и напряжения, которые связаны с амплитудными значениями следующими соотношениями:
Осциллограф (ОС) используется для визуального наблюдения изменения частоты вынужденных колебаний и амплитуды напряжения на емкости и индуктивности. Исследуемый контур подключается к ЗГ, mА, ЦВ и ОС с помощью шнуров, имеющих на конце по два штекера.
7.3. Задание и отчетность
1) Собрать схему согласно рис.7.5. Начальное положение ручек приборов указано на рабочем месте. Там же приведены все необходимые данные. 2) При заданных значениях L и С рассчитать резонансную частоту. 3) Снять резонансные кривые Im = Im(n), Ucm = Ucm(n), ULm = ULm(n) для двух значений R при постоянном выходном напряжении ЗГ. При этом следует учитывать сопротивление амперметра и активное сопротивление катушки. Отсчет частоты по шкале ЗГ следует делать через 5 Гц вблизи резонансной частоты и через 10 Гц вдали от нее. 4) Построить кривые Im= Im(n) для обоих значений R на одном графике, определить по графикам nр и сравнить ее с расчетной. Убедиться, что nр зависит только от L и С. 5) Построить аналогичные кривые для Ucm и ULm также на одном рисунке. Определить по графикам ncр, nLр и nр. Убедиться, что ncр и nLр зависят от величины R при фиксированных L и C. 6) Определить добротность контура Q1 и Q2 при значениях R1 и R2 согласно соотношению (7.14). 7) Дополнительное задание. Определить добротность контура Q1 и Q2 при R1 и R2 из графиков I = I(n) по формуле (7.18). Сравнить полученные значения с результатами, полученными в п.6.
7.4. Контрольные вопросы
1. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и решите его. 2. От чего зависит амплитуда вынужденных колебаний? Что называется резонансом? Какова его роль? 3. Как определяются резонансные частоты nр, ncр и nLр? 4. Нарисуйте и объясните векторную диаграмму для цепи с последовательным включенным резистором, катушкой индуктивности и конденсатором. 5. Чему равно полное сопротивление контура? От чего зависит индуктивное сопротивление, емкостное сопротивление? 6. Что показывает добротность контура и как ее определяют?
Литература. [1, §§ 22.1, 22.2; 2, §§ 51; 3, §§ 91]
8. ИССЛЕДОВАНИЕ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ РЕЗОНАНСА
Цель работы: изучение колебаний струны с закрепленными концами; исследование зависимости скорости распространения поперечных колебаний в струне от ее натяжения. Приборы и принадлежности: закрепленная на штативе струна, чашка для грузов, набор разновесов, генератор ГЗ-33, постоянный магнит, линейка, микрометр.
8.1. Теоретические сведения
Рассмотрим струну, закрепленную с одного конца (рис.8.1). Если свободный конец струны (х = 0) смещать вдоль оси y по гармоническому закону у = Аsinwt, где А - амплитуда колебаний, w = 2p/T - циклическая частота (Т - период колебаний), то вследствие взаимодействия между частицами струны колебания начнут распространяться вдоль струны с некоторой скоростью u. При этом частицы струны в точках x будут совершать поперечные колебания по закону y1(x,t) = A sin [ t - (x / u) ],
где отношение x/u дает время, на которое колебания в точке х запаздывают относительно колебаний частиц в точке x = О.
Процесс распространения колебаний называют волной. Расстояние l, которое волна проходит за период Т, называют длиной волны: l = u Т. На рис.8.2.а показана струна в момент, когда возмущение (в данном случае оно имеет вид полуволны) дошло до закрепленного конца. Если бы струна продолжалась дальше, то "горбик" продолжал бы двигаться вправо, оставаясь при этом сверху. На рис. 8.2.б показана струна (ее конфигурация) еще через 1/2 Т. После отражения "горбик" бежит в обратном направлении, находясь уже снизу. Последнее означает изменение фазы колебания (аргумента синуса) на p Уравнение отраженной волны имеет вид y2(x,t) = Asin{w[t -(2L - x)/u -p]} = - Asinw[t-(2L - x)/u]. Отношение (2L - x)/u равно времени, которое требуется волне, чтобы пройти от свободного конца до точки закрепления и вернуться в точку x. В соответствии с принципом суперпозиции результирующие колебания частиц струны в точке x найдем, сложив y1 и y2. Используя тождество
и учитывая, что w/u= 2p/l, получим
Этот колебательный процесс называется стоячей волной. Формула (8.1) показывает, что множитель
(к узлам падающая волна и отраженная приходят в противофазе). В частности, при n = 0 х = L, т.е. точка закрепления струны является узлом, как и должно быть. Посередине между узлами амплитуда колебаний максимальная и равна 2 А. Эти точки - их называют пучностями - определяются из условия
(к этим точкам колебания приходят в фазе). Таким образом, узлы, также как и пучности - находятся друг от друга на расстоянии полуволн. Все частицы струны между двумя соседними узлами колеблются синфазно, а колебания частиц по разные стороны от узла совершаются в противофазе.
закрепления расположены узлы. Поэтому в струне с заметной интенсивностью возбуждаются колебания только таких частот, при которых на длине струны L укладывается целое число полуволн, т.е. когда
Учитывая связь l с частотой n и скоростью распространения волны u, можно записать:
Частоты nn называют собственными частотами колебаний струны. Самая низкая собственная частота n1= Скорость распространения поперечных колебаний вдоль струны зависит от натяжения струны и определяется формулой
где Т - натяжение струны (в равновесном состоянии), r - плотность материалы струны, S - поперечное сечение струны, или
где d - диаметр струны. Для возбуждения колебаний в струне в данной работе используется явление резонанса, которое заключается в следующем: если частота вынуждающей силы, приложенной к малому участку струны, совпадает с одной из собственных частот струны, а место приложения - с одной из пучностей, то в струне устанавливается колебательный процесс (стоячая волна) с максимальной амплитудой колебаний. Вынуждающей силой Ампера
где I - сила тока в струне, Таким образом (вспомните определение векторного произведения), DF = I Dl В sina,
8.2. Описание установки
В установке, схематически показанной на рис.8.5, струна натягивается между стойками подставки, причем один конец ее закреплен неподвижно, а к другому прикреплена чашка с грузами, создающими натяжение в струне.
положение магнита - с пучностью стоячей волны, то наблюдается явление резонанса Ручки управления звуковым генератором расположены на его передней панели. Частота колебаний устанавливается поворотом ручки переключателя "Множитель" (ступенчатая регулировка) и поворотом лимба (плавная регулировка). Для определения частоты ЗГ в герцах нужно отсчет по шкале лимба умножить на показание переключателя "Множитель". Напряжение на выходе ЗГ регулируется "Рег.вых.напр." (плавная регулировка) и ступенями, при помощи переключения аттенюатора (делителя), имеющего гравировку "Пределы шкалы" - "Ослабление дБ". Основная погрешность прибора по частоте ∆ν = ± (0,02 ∙ F + 1) Гц, где F - показание шкалы лимба.
8.3. Порядок выполнения работы
1) Включить генератор. 2) Создать натяжение в струне, поместив на чашку для грузов разновески так, чтобы суммарная масса была равна примерно 50 г. 3) С помощью линейки измерить длину рабочей части струны, то есть расстояние от одной стойки до другой. Измерить микрометром диаметр струны в различных точках рабочего участка 5 раз и в качестве диаметра взять среднее из этих измерений. 4) По формуле (8.7) вычислить теоретическое значение скорости распространения колебаний в струне для данного натяжения Т. Результаты занести в таблицу 3 (в графу 5) После прогрева генератора ручкой "Множитель" и поворотом лимба звукового генератора установить частоту основного тона ν1. Установив магнит посредине струны и плавно изменяя частоту вращением лимба генератора, добиться устойчивых колебаний основного тона. Соответствующее значение ν1эксп, определенное по шкале генератора, занести в таблицу 3 (в графу νэксп). Аналогично найти ν2эксп и ν3эксп. Для этого, передвигая магнит и меняя частоту ЗГ вблизи рассчитанных предварительно ν2 и ν3, добиться устойчивых колебаний второго и третьего обертонов. Определенные по шкале ЗГ частоты ν2эксп и ν3эксп занести в таблицу 3. Если амплитуда колебаний окажется малой, следует увеличить выходное напряжение генератора. Таблица 3
6) Провести аналогичные измерения при других натяжениях нити еще 4 раза (пункты 4 и 5), увеличивая массу разновесок каждый раз на 30 г. 7) По экспериментальным данным найти скорости распространения поперечных колебаний для каждого натяжения струны по формуле
8) Построить (на одном рисунке) графики зависимости
8.4. Контрольные вопросы
1. Что такое волна? Какие волны называют поперечными? 2. Как определяется длина волны? 3. Как получаются стоячие волны? Что такое узлы? пучности? 4. Какую частоту называют основной? Обертоном? 5. От чего зависит скорость распространения поперечных колебаний вдоль струны? 6. Как используется явление резонанса в данной работе? 7. Как определяется сила Ампера в данной работе? 8. Каково назначение постоянного магнита и ЗГ в установке? 9. Как выглядит закрепленная с обоих концов струна, если в ней установились колебания основного тона? 1-го, 2-го обертонов? 10. Объясните вывод уравнения стоячей волны.
Литература. [1, §§ 14.2; 2, §§ 54; 3, §§ 44, 93, 99, 100] ЛИТЕРАТУРА
1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики: Учебное пособие для втузов. В 3-х т. - Изд. 4-е, перераб. - М.: Высшая школа, 1977. Т.2: Электричество и магнетизм. 375 с. 2. Зисман Т.А., Тодес О.М. Курс общей физики.Т.2. М.: Наука, 1972. 366 с. 3. Савельев И.В. Курс общей физики: Для втузов. В 3-х т. М.: Наука, 1978. Т.2: Электричество и магнетизм. Волны. Оптика. 480 с. 4. Трофимова Т.Н, Курс физики: Учебное пособие для вузов. 4-е изд., испр. М.: Высшая школа, 1997. 542 с.
СОДЕРЖАНИЕ
|

 . (7.9)
. (7.9) , (7.10)
, (7.10) - полное сопротивление цепи, а ωL-(1/ωC) - реактивное сопротивление. ХL = ωL и Хc = 1/ωC называют индуктивным и емкостным сопротивлением соответственно. Смысл названия "полное сопротивление" в том, что амплитудные значения Um и Im связаны между собой соотношением, подобным закону Ома: Im = Um/Z. Из соотношения (7.10) видно, что при
- полное сопротивление цепи, а ωL-(1/ωC) - реактивное сопротивление. ХL = ωL и Хc = 1/ωC называют индуктивным и емкостным сопротивлением соответственно. Смысл названия "полное сопротивление" в том, что амплитудные значения Um и Im связаны между собой соотношением, подобным закону Ома: Im = Um/Z. Из соотношения (7.10) видно, что при  амплитуда тока Im достигает максимального значения Im max = Um/R, а угол φ = O. Кривую зависимости Im от ωназывают резонансной кривой, а частоту
амплитуда тока Im достигает максимального значения Im max = Um/R, а угол φ = O. Кривую зависимости Im от ωназывают резонансной кривой, а частоту  , при которой Im=Im max, резонансной частотой. Чем меньше R, тем больше Im при резонансе и тем острее резонансная кривая (рис.7.3.а).
, при которой Im=Im max, резонансной частотой. Чем меньше R, тем больше Im при резонансе и тем острее резонансная кривая (рис.7.3.а). а)
а)
 б)
б)
 . (7.11)
. (7.11)
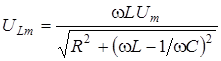 . (7.12)
. (7.12) получаем:
получаем: и
и  (7.13)
(7.13) (7.14)
(7.14) ,
,  . (7.15)
. (7.15)

 , (7.16)
, (7.16)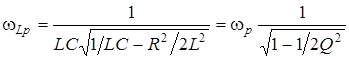

 Рис.7.4
Рис.7.4
 (7.18)
(7.18)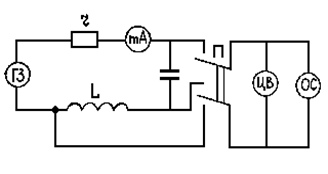 Рис.7.5
Рис.7.5
 ,
, 

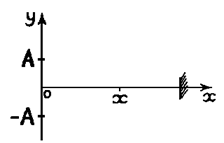 Рис.8.1
Рис.8.1
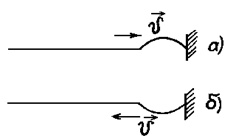 Рис.8.2
Рис.8.2
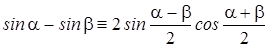
 . (8.1)
. (8.1) , выражающий периодическое изменение во времени, не зависит от координаты, а амплитуда колебаний
, выражающий периодическое изменение во времени, не зависит от координаты, а амплитуда колебаний  различна для разных точек струны. Из выражения (8.1) следует, что на струне имеется ряд точек, которым соответствует амплитуда, равная нулю. Эти точки (их называют узлами) определяются из условия:
различна для разных точек струны. Из выражения (8.1) следует, что на струне имеется ряд точек, которым соответствует амплитуда, равная нулю. Эти точки (их называют узлами) определяются из условия: или
или  , n = 0, 1, 2, … (8.2)
, n = 0, 1, 2, … (8.2) или
или  , n = 0,1,2,… (8.3)
, n = 0,1,2,… (8.3) Рис.8.3
Рис.8.3
 или
или  , n = 1, 2, … (8.4)
, n = 1, 2, … (8.4) , n = 1, 2,... (8.5)
, n = 1, 2,... (8.5) /2L называется основной частотой или основным тоном (n=1). Более высокие частоты, кратные n1, называютсяn1 - первой, n2 - второй, n3 - третьей и т.д. гармониками.
/2L называется основной частотой или основным тоном (n=1). Более высокие частоты, кратные n1, называютсяn1 - первой, n2 - второй, n3 - третьей и т.д. гармониками. , (8.6)
, (8.6)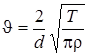 , (8.7)
, (8.7) , действующая на отрезок струны Dl, расположенный между полюсами постоянного магнита. По закону Ампера
, действующая на отрезок струны Dl, расположенный между полюсами постоянного магнита. По закону Ампера , (8.8)
, (8.8) - вектор, его направление совпадает с направлением тока,
- вектор, его направление совпадает с направлением тока,  - индукция магнитного поля.
- индукция магнитного поля. Рис.8.4
Рис.8.4
 Рис.8.5
Рис.8.5
 ). Используя вычисленное значение скорости
). Используя вычисленное значение скорости  рассчитать частоту основного тока ν1. Значение ν1 вписать в таблицу 3 (в графу νтеор). Туда же занести найденные по формуле (84) значения следующих обертонов ν2 и ν3 (при n = 2 и n = 3).
рассчитать частоту основного тока ν1. Значение ν1 вписать в таблицу 3 (в графу νтеор). Туда же занести найденные по формуле (84) значения следующих обертонов ν2 и ν3 (при n = 2 и n = 3).

 натяжение струны Т = Р = mg, m - масса груза) и сделать выводы.
натяжение струны Т = Р = mg, m - масса груза) и сделать выводы.


