Нахождение области определения функции.
Сначала строим асимптоты, наносим точки локальных максимумов и минимумов функции, точки перегиба и промежуточные точки. Для удобства построения графика можно нанести и схематическое обозначение промежутков возрастания, убывания, выпуклости и вогнутости, не зря же мы проводили исследование функции =).
Осталось провести линии графика через отмеченные точки, приближая к асимптотам и следуя стрелочкам.
Домашнее задание: Провести полное исследование функций и построить их график: 1) 2) Частотные критерии устойчивости Михайлова, Найквиста, D-разбиения по одному параметру.
Лекция___. Полное исследование функции и построение ее графика Задача: провести полное исследование функции и построить ее график
Алгоритм исследования функции Нахождение области определения функции. Определение 1. Область определения функции - множество, на котором задаётся функция. Определение 2. Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения. Определение 3. Пусть задано отображение f, которое отображает множество X в Y, то есть: множество X называется областью определения функции f и обозначается D(f), или dom f (от англ. domain «область»). Правила нахождения области определения функции: Пусть y=f(x) и y=g(x) - основные элементарные функции или их комбинации. Для степенных функций вида
Для логарифмических функций вида
Для дробей вида
Для функций тангенса или котангенса вида tg(f(x)) или ctg(f(x)) область определения находится из систем соответственно:
Для функций арксинус или арккосинус вида arcsin(f(x)) или arccos(f(x)) область определения находится из системы (т.к. областью определения арксинуса и арккосинуса является отрезок от -1 до 1):
Для показательно степенных функций вида вида
Область определения суммы (разности) функций вида
Область определения комбинации рассмотренных выше функций вида
|








 .
. ; тогда
; тогда , где n - четное, область определения находится из системы:
, где n - четное, область определения находится из системы:
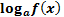 область определения находится из системы:
область определения находится из системы:
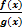 область определения находится из системы:
область определения находится из системы:
 или
или 



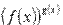 область определения находится из системы:
область определения находится из системы:
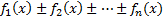 находится из системы:
находится из системы:
 находится из системы:
находится из системы:





