Промежутки вогнутости и выпуклости функции находятся при решениями неравенств  и
и 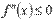 соответственно. Иногда вогнутость называют выпуклостью вниз, а выпуклость – выпуклостью вверх.
соответственно. Иногда вогнутость называют выпуклостью вниз, а выпуклость – выпуклостью вверх.
Таким образом, чтобы определить промежутки вогнутости и выпуклости функции:
1) находим вторую производную;
2) находим нули числителя и знаменателя второй производной;
3) разбиваем область определения полученными точками на интервалы;
4) определяем знак второй производной на каждом из промежутков. Знак «+» будет соответствовать промежутку вогнутости, знак «-» - промежутку выпуклости.
Определение 11. Точка 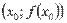 называется точкой перегиба, если в данной точке существует касательная к графику функции и вторая производная функции меняет знак при прохождении через
называется точкой перегиба, если в данной точке существует касательная к графику функции и вторая производная функции меняет знак при прохождении через 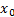 . Т.е. точками перегиба могут являться точки, проходя через которые вторая производная меняет знак, в самих точках либо равна нулю, либо не существует, но эти точки входят в область определения функции.
. Т.е. точками перегиба могут являться точки, проходя через которые вторая производная меняет знак, в самих точках либо равна нулю, либо не существует, но эти точки входят в область определения функции.
Находим вторую производную на области определения.
 Далее ищем нули числителя и знаменателя.
В нашем примере нулей числителя нет, нули знаменателя
Далее ищем нули числителя и знаменателя.
В нашем примере нулей числителя нет, нули знаменателя  .
Наносим эти точки на числовую ось и определяем знак второй производной внутри каждого полученного промежутка. .
Наносим эти точки на числовую ось и определяем знак второй производной внутри каждого полученного промежутка.
 Делаем вывод:
- функция выпуклая на промежутке
Делаем вывод:
- функция выпуклая на промежутке  .
- функция вогнутая на промежутке .
- функция вогнутая на промежутке 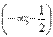 и на промежутке и на промежутке 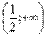 .
В нашем примере точек перегиба нет, так как вторая производная меняет знак, проходя через точки .
В нашем примере точек перегиба нет, так как вторая производная меняет знак, проходя через точки  ., а они не входят в область определения функции. ., а они не входят в область определения функции.
|

 и
и 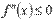 соответственно. Иногда вогнутость называют выпуклостью вниз, а выпуклость – выпуклостью вверх.
соответственно. Иногда вогнутость называют выпуклостью вниз, а выпуклость – выпуклостью вверх.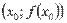 называется точкой перегиба, если в данной точке существует касательная к графику функции и вторая производная функции меняет знак при прохождении через
называется точкой перегиба, если в данной точке существует касательная к графику функции и вторая производная функции меняет знак при прохождении через 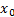 . Т.е. точками перегиба могут являться точки, проходя через которые вторая производная меняет знак, в самих точках либо равна нулю, либо не существует, но эти точки входят в область определения функции.
. Т.е. точками перегиба могут являться точки, проходя через которые вторая производная меняет знак, в самих точках либо равна нулю, либо не существует, но эти точки входят в область определения функции. Далее ищем нули числителя и знаменателя.
В нашем примере нулей числителя нет, нули знаменателя
Далее ищем нули числителя и знаменателя.
В нашем примере нулей числителя нет, нули знаменателя  .
Наносим эти точки на числовую ось и определяем знак второй производной внутри каждого полученного промежутка.
.
Наносим эти точки на числовую ось и определяем знак второй производной внутри каждого полученного промежутка.
 Делаем вывод:
- функция выпуклая на промежутке
Делаем вывод:
- функция выпуклая на промежутке  .
- функция вогнутая на промежутке
.
- функция вогнутая на промежутке 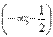 и на промежутке
и на промежутке 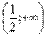 .
В нашем примере точек перегиба нет, так как вторая производная меняет знак, проходя через точки
.
В нашем примере точек перегиба нет, так как вторая производная меняет знак, проходя через точки 


