Простейшие свойства определителя.

. Определитель треугольной матрицы равен произведению диагональных элементов.

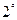. При транспонировании квадратной матрицы значение определителя не меняется, т.е. .

. При перестановке двух столбцов (строк) в матрице ее детерминант меняет знак.

. Определитель, имеющий два одинаковых столбца(строки), равен нулю.

. Если одна из строк(столбцов) матрицы полностью состоит из нулей, то ее определитель равен нулю.

. Общий множитель у всех элементов столбца (строки) можно вынести за знак определителя, т.е. при умножении строки (столбца) матрицы на число ее определитель умножается на это число.

. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то определитель матрицы равен нулю.

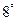. Если к какой-либо строке (столбцу) матрицы прибавить линейную комбинацию других ее строк (столбцов), то ее определитель не изменится.

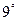. Если элементы -го столбца матрицы представляют собой линейную комбинацию вида , то , где матрицы 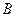и получаются из матрицы путем замены -го столбца на элементы и .

. Если в определителе выбрать какую-либо строку (столбец), то определитель равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения, т.е.

-

разложение по i -й строке,

-

разложение по j -му столбцу.

. Сумма произведений какой либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.

. Определитель произведения матриц равен произведению их определителей, т.е. .