1.1. Перестановки. Упорядоченная совокупность чисел  , в которой
, в которой
1)  ,
,  ;
;
2) 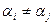 при
при  ,
,
называется перестановкой из чисел 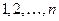 .
.
Перестановка 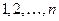 называется натуральной. Преобразование перестановки, при котором два ее числа
называется натуральной. Преобразование перестановки, при котором два ее числа  и
и  с номерами
с номерами  меняются местами, называется транспозицией.
меняются местами, называется транспозицией.
1.2. Говорят, что два числа  и
и  в перестановке
в перестановке  образуют инверсию (беспорядок), если большее из них предшествует меньшему, т.е. если
образуют инверсию (беспорядок), если большее из них предшествует меньшему, т.е. если 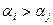 при
при  , и порядок – в противном случае, т.е. если
, и порядок – в противном случае, т.е. если  при
при  . Перестановка называется четной, если общее число инверсий в ней четно, и нечетной – в противном случае. Общее число инверсий в перестановке
. Перестановка называется четной, если общее число инверсий в ней четно, и нечетной – в противном случае. Общее число инверсий в перестановке  обозначается символами
обозначается символами  или
или  .
.
1.3.Теорема. Число всевозможных перестановок из 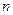 чисел равно
чисел равно 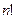 .
.
1.4. Теорема. Каждая транспозиция меняет четность перестановки.
1.5. Рассмотрим систему величин  (или
(или  ), которые по определению раны нулю, если содержат два или большее число равных индексов, и равны +1 или -1, в зависимости от того, четная или нечетная перестановка
), которые по определению раны нулю, если содержат два или большее число равных индексов, и равны +1 или -1, в зависимости от того, четная или нечетная перестановка  . Данные символы называются символами Леви-Чивитта. Можно сказать, что
. Данные символы называются символами Леви-Чивитта. Можно сказать, что
 ,
,
и при одинаковых значениях индексов  равен нулю.
равен нулю.
Символ 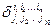 =
= 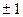 , если
, если 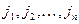 есть некоторая перестановка значений индексов
есть некоторая перестановка значений индексов  , считая, что все эти значения различны; при этом берется +1, если перестановка четная и -1, если нечетная. Во всех остальных случаях
, считая, что все эти значения различны; при этом берется +1, если перестановка четная и -1, если нечетная. Во всех остальных случаях 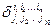 =0 (т. е. если среди значений
=0 (т. е. если среди значений  или среди значений
или среди значений 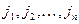 есть одинаковые, а также среди значений
есть одинаковые, а также среди значений  есть такие, каких нет среди
есть такие, каких нет среди 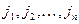 и наоборот). Данный символ называется обобщенным символом Кронекера(альтернатором). Имеем
и наоборот). Данный символ называется обобщенным символом Кронекера(альтернатором). Имеем
 =
= 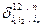 ,
,
 =
= 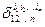 .
.
1.6. Пусть А – квадратная матрица  - го порядка. Рассмотрим произведение элементов этой матрицы, взятых по одному из каждой строки и каждого столбца
- го порядка. Рассмотрим произведение элементов этой матрицы, взятых по одному из каждой строки и каждого столбца  .
.
Заметим, что в этом произведении сомножители упорядочены в порядке возрастания номеров строк, при этом номера столбцов  образуют перестановку из чисел
образуют перестановку из чисел 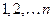 , так как
, так как 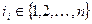 и
и 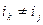 при
при  . Произведений такого вида в матрице
. Произведений такого вида в матрице  столько, сколько существует перестановок
столько, сколько существует перестановок  из
из 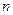 чисел, т.е.
чисел, т.е. 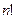 .
.
Определителем (детерминантом) квадратной матрицы 
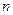 -го порядка называется сумма
-го порядка называется сумма 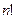 произведений элементов матрицы, выбранных по одному из каждого столбца и каждой строки, причем если сомножители в этом произведении упорядочены в порядке возрастания номеров строк, то оно берется со знаком плюс в случае четной перестановки номеров столбцов и со знаком минус в случае нечетной перестановки.
произведений элементов матрицы, выбранных по одному из каждого столбца и каждой строки, причем если сомножители в этом произведении упорядочены в порядке возрастания номеров строк, то оно берется со знаком плюс в случае четной перестановки номеров столбцов и со знаком минус в случае нечетной перестановки.
Обозначение: 
Итак,
 ,
,
где суммирование ведется по всевозможным перестановкам  .
.
С помощью введенного обобщенного символа Кронекера, определитель может быть записан в одном из двух видов:
 или
или
 .
.
1.7. Вычислим определитель второго порядка
 .
.
По определению альтернатора 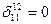 ,
, 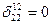 ,
,  ,
,  . Поэтому для определителя второго порядка имеем
. Поэтому для определителя второго порядка имеем
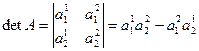 ,
,
или в другой записи
 .
.
1.8. Для определителя третьего порядка:


 =
=

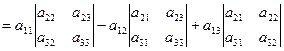 .
.
1.9. Если в квадратной матрице 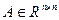 зачеркнуть
зачеркнуть 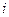 -строку и
-строку и  -столбец, то получим матрицу
-столбец, то получим матрицу  -го порядка. Определитель этой матрицы называется минором элемента
-го порядка. Определитель этой матрицы называется минором элемента  определителя матрицы
определителя матрицы  и обозначается через
и обозначается через  .
.
1.10. Алгебраическим дополнением элемента  определителя матрицы
определителя матрицы  называется величина
называется величина  .
.

 , в которой
, в которой ,
,  ;
;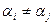 при
при  ,
,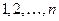 .
. и
и  с номерами
с номерами 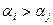 при
при  , и порядок – в противном случае, т.е. если
, и порядок – в противном случае, т.е. если  при
при  или
или  .
.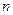 чисел равно
чисел равно 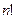 .
. (или
(или  ), которые по определению раны нулю, если содержат два или большее число равных индексов, и равны +1 или -1, в зависимости от того, четная или нечетная перестановка
), которые по определению раны нулю, если содержат два или большее число равных индексов, и равны +1 или -1, в зависимости от того, четная или нечетная перестановка  . Данные символы называются символами Леви-Чивитта. Можно сказать, что
. Данные символы называются символами Леви-Чивитта. Можно сказать, что ,
,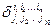 =
= 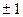 , если
, если 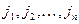 есть некоторая перестановка значений индексов
есть некоторая перестановка значений индексов 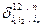 ,
,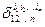 .
. - го порядка. Рассмотрим произведение элементов этой матрицы, взятых по одному из каждой строки и каждого столбца
- го порядка. Рассмотрим произведение элементов этой матрицы, взятых по одному из каждой строки и каждого столбца  .
.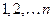 , так как
, так как 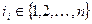 и
и 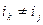 при
при  . Произведений такого вида в матрице
. Произведений такого вида в матрице  столько, сколько существует перестановок
столько, сколько существует перестановок 

 ,
, или
или .
. .
.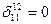 ,
, 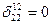 ,
,  ,
,  . Поэтому для определителя второго порядка имеем
. Поэтому для определителя второго порядка имеем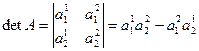 ,
, .
.

 =
=
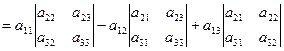 .
.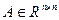 зачеркнуть
зачеркнуть 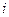 -строку и
-строку и  -столбец, то получим матрицу
-столбец, то получим матрицу  -го порядка. Определитель этой матрицы называется минором элемента
-го порядка. Определитель этой матрицы называется минором элемента  определителя матрицы
определителя матрицы  .
.  .
.


