Методические указания. Модуляция в радиотехнике – изменение какого-либо одного или нескольких параметров колебания высокой частоты в соответствии с законом передаваемого сообщения
Модуляция в радиотехнике – изменение какого-либо одного или нескольких параметров колебания высокой частоты в соответствии с законом передаваемого сообщения (в соответствии с передаваемым сигналом). Передаваемый сигнал при этом называется модулирующим или управляющим, а высокочастотный сигнал, подвергающийся модуляции, называется несущим, так как он как бы на себе "несет" передаваемый сигнал. Результатом модуляции является модулированный сигнал. При амплитудной модуляции (АМ) по закону передаваемого сообщения изменяется амплитуда высокочастотного сигнала. При гармоническом управляющем сигнале полное выражение для АМ-колебания имеет вид:
Величина
Раскрывая квадратные скобки в выражении (4), после преобразования получим
Амплитудная спектральная диаграмма этого сигнала приведена на рисунке 1. Если модулирующий сигнал многочастотный, то аналогичные преобразования позволяют строить амплитудную спектральную диаграмму для этого случая. Следует обратить внимание на то, что уровни составляющих спектра на частотах
Рисунок 1
При частотной модуляции (ЧМ) по закону передаваемого сообщения изменяется частота высокочастотного сигнала. Если модулирующий сигнал гармонический с частотой
Величина
Используя известное из математики соотношение
из выражения (6) получим
где Как видно из полученного выражения, спектр ЧМ-сигнала состоит из бесконечно большого числа составляющих, расположенных на шкале частот по обе стороны от частоты При Для определения состава спектра существенно следующее свойство функций Бесселя: значения функций при Указанное свойство определяет ширину спектра, так как позволяет ограничить спектр
В справочниках по высшей математике даны значения функций Бесселя только для положительных значений
Однако необходимо помнить, что амплитуда – величина положительная, поэтому амплитудная спектральная диаграмма должна строиться для абсолютных значений, т.е. для Общая практическая ширина спектра
Очевидно, что число гармонических составляющих в пределах ширины спектра равно Пример амплитудной спектральной диаграммы ЧМ - сигнала для
Рисунок 2
Из рассмотрения примера видно, что при частотной модуляции уровни боковых составляющих могут превышать уровень несущего сигнала. Ширина спектра равна, очевидно,
Несущим сигналом при АИМ является периодическая последовательность прямоугольных импульсов электрического тока. В качестве информационного параметра этой последовательности используется амплитуда импульсов. АИМ широко используется в многоканальных системах передачи информации с временным разделением каналов как промежуточная операция преобразования аналоговых (непрерывных) сигналов в цифровые. Модулирующие сигналы в этом случае, как правило, являются аналоговыми. Операция, которая осуществляется с помощью АИМ, является операцией дискретизации по времени первичного сигнала. Поэтому для того, чтобы модулированный сигнал на выходе амплитудно-импульсного модулятора содержал всю информацию, находящуюся в модулирующем сигнале, и эту информацию можно было выделить при демодуляции, исходная импульсная последовательность должна удовлетворять требованиям теоремы Котельникова, т.е. частота следования импульсов
Последовательность импульсов имеющих амплитуду
Подставив (11) в (3), получим
где
Каждый член суммы в (12) представляет собой сумму трех спектральных составляющих: составляющую на частоте дискретизации или ее гармоники и составляющие на суммарной и разностной частотах:
Таким образом из выражений 12 и 14 следует, что амплитудный спектр АИМ состоит из: - составляющей на нулевой частоте (постоянной составляющей), - составляющих модулирующего сигнала (второе слагаемое в выражении (12)), - составляющих на частоте дискретизации - боковых составляющих около каждой гармоники частоты дискретизации на частотах При построение амплитудной спектральной диаграммы АИМ при вычислении
Например, задан модулирующий сигнал
Рисунок 3 – Амплитудная спектральная диаграмма АИМ
|


 . (4)
. (4) называется коэффициентом модуляции. Для неискаженного приема должно выполняться условие
называется коэффициентом модуляции. Для неискаженного приема должно выполняться условие  .
.
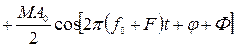 (5)
(5) и
и  (боковых составляющих) не могут превышать половины уровня несущего колебания.
(боковых составляющих) не могут превышать половины уровня несущего колебания.
 , то выражение для частотно-модулированного колебания имеет вид:
, то выражение для частотно-модулированного колебания имеет вид: . (6)
. (6) называется индексом модуляции. Индекс модуляции
называется индексом модуляции. Индекс модуляции  аналогичен коэффициенту амплитудной модуляции
аналогичен коэффициенту амплитудной модуляции  , но в отличие от него обычно много больше единицы, но может быть и малым (до нуля). Индекс модуляции
, но в отличие от него обычно много больше единицы, но может быть и малым (до нуля). Индекс модуляции  (максимальным отклонением частоты от своего среднего значения
(максимальным отклонением частоты от своего среднего значения  ) следующим выражением
) следующим выражением .
.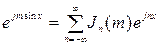 ,
, , (7)
, (7) - функции Бесселя первого рода
- функции Бесселя первого рода  -го порядка от аргумента
-го порядка от аргумента  :
:  при
при  (Необходимо обратить внимание на то, что спектр АМ-сигнала содержит только три составляющих, если модулирующий сигнал гармонический).
(Необходимо обратить внимание на то, что спектр АМ-сигнала содержит только три составляющих, если модулирующий сигнал гармонический).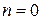 получается колебание несущей частоты
получается колебание несущей частоты  определяются произведениями амплитуды несущего колебания
определяются произведениями амплитуды несущего колебания  на соответствующие функции Бесселя. Они зависят от номера составляющей
на соответствующие функции Бесселя. Они зависят от номера составляющей  .
. настолько малы, что ими можно пренебречь.
настолько малы, что ими можно пренебречь. -й составляющей в обе стороны от несущей. Например, для
-й составляющей в обе стороны от несущей. Например, для  выражение (7) примет вид
выражение (7) примет вид . (8)
. (8) при
при  при
при  .
. равна произведению расстояния между составляющими на число таких расстояний, т.е.
равна произведению расстояния между составляющими на число таких расстояний, т.е. . (9)
. (9) .
. приведена на рисунке 2.
приведена на рисунке 2.
 .
. (частота дискретизации) должна быть, по крайней мере в 2 раза больше, чем верхняя частота в спектре первичного сигнала
(частота дискретизации) должна быть, по крайней мере в 2 раза больше, чем верхняя частота в спектре первичного сигнала  . Обычно эту частоту выбирают из соотношения
. Обычно эту частоту выбирают из соотношения (10)
(10) , длительность
, длительность  , следующих друг за другом с периодам повторения
, следующих друг за другом с периодам повторения  , может быть представлена рядом Фурье
, может быть представлена рядом Фурье . (11)
. (11) , (12)
, (12) . (13)
. (13) . (14)
. (14) и ее гармоник
и ее гармоник  ,
, и
и  .
. в выражении (13) для
в выражении (13) для  и
и  можно приближенно положить
можно приближенно положить



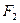 . В этом случае выбираем частоту дискретизации
. В этом случае выбираем частоту дискретизации  . Амплитудная спектральная диаграмма АИМ показана на рисунке 3.
. Амплитудная спектральная диаграмма АИМ показана на рисунке 3.



