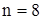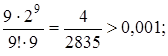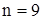ТИПЫ ФУНКЦИЙ
Продолжение табл.1.7
Разложим каждое слагаемое в ряд
Определим, сколько слагаемых надо взять в каждом разложении, чтобы достигнуть заданной точности. Ряд (2.1) – знакочередующийся ряд лейбницевского типа, поэтому воспользуемся оценкой Лейбница для остатка ряда: |Rn| £ a n+1. Первый отброшенный член не должен превосходить 0,001 n = 3 Значит, нам достаточно взять первые два слагаемых. Ln 1,1» 0,1 – 0,5×10-2 = 0,1 – 0,005 = 0,095. Ряды (2.2) – (2.4) являются знакоотрицательными рядами, поэтому оценкой Лейбница воспользоваться нельзя. Оценим Ln(1 + x) сверху геометрической прогрессией Тогда
Воспользуемся оценкой (2.5) для рядов (2.2) – (2.4). Для ряда (2.2)
Это верно для n = 10. Следовательно, надо в разложении взять 10 слагаемых для достижения заданной точности 0,001.
Для ряда (2.3) Неравенство верно для n = 6. Значит, надо взять лишь 6 слагаемых разложения
Для ряда (2.4)
Это верно для n = 8. Следовательно,
Итак,
Таким образом, 1,703 < Ln 5,5 < 1,705.
2.2. Пример 2
Вычислить значение определенного интеграла Интеграл J является несобственным. Так как Разложим подынтегральную функцию в ряд и почленно проинтегрируем
Определим, сколько слагаемых надо взять, чтобы погрешность вычислений не превышала 0,001. Для этого применим метод мажорирования.
Для n = 5
-0,5817 < J < -0,5797.
2.3. Пример 3 Вычислить значение определенного интеграла Интеграл y является несобственным. Так как Обозначим
где
Так как
Значит,
где Оценим
Теперь подберем n так, чтобы
Для этого n будем иметь
Необходимо взять в сумме 9 слагаемых, и необходимая точность будет достигнута. 3. Контрольные вопросы
1. Что называется функциональным рядом? 2. Область сходимости функционального ряда. 3. Ряд Тейлора для функции f (x) по степеням х – а. 4. Что называется степенным рядом? 5. Область сходимости степенного ряда. Теорема Абеля. 6. Оценка остатка функционального ряда. 7. Применение степенных рядов к приближенным вычислениям. 8. Теорема о непрерывности суммы функционального ряда. 9. Теорема о почленном интегрировании и почленном дифференцировании функционального ряда. 10. Равномерная сходимость степенного ряда. Теорема Вейерштрасса. 11. Разложение в ряд основных функций: ex, Cos x, Sin x, Ln(1+x), (1+x)m. 12. Условия разложимости функций в ряд Тейлора.
Библиографический список
1. Пискунов Н.И. Дифференциальное и интегральное исчисления для втузов. Т.2. М.: Наука, 1970-1976. 2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисления. М.: Наука, 1980. 3. Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1971. 4. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. Ч. 2. М.: Высш., шк., 1971. 5. Задачи и упражнения по математическому анализу для втузов. / Под ред. Б.П. Демидовича. М.: Наука, 1978. 6. Запорожец Г.И. Руководство к решению задач по математическому анализу. М. Высш. шк., 1966. 7. Сборник задач по математике для втузов. Специальные разделы. / Под ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1981. 8. Шмелев П.А. Теория рядов в задачах и упражнениях. М.: Высш. шк., 1983.
|


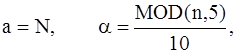
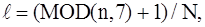

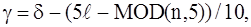

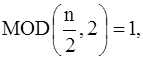 то продолжаем четным образом.
Если
то продолжаем четным образом.
Если  то продолжаем нечетным образом.
то продолжаем нечетным образом.
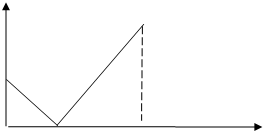

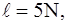
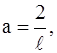

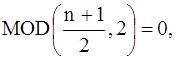 то продолжаем четным образом.
Если
то продолжаем четным образом.
Если 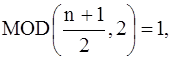 то продолжаем нечетным образом.
то продолжаем нечетным образом.

 1
1

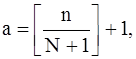

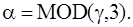
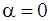 , функция продолжается четным образом.
, функция продолжается четным образом.
 , функция продолжается нечетным образом.
, функция продолжается нечетным образом.
 период функции.
период функции.
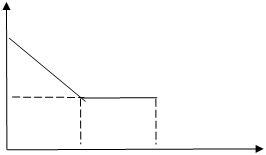
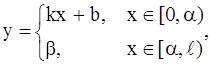

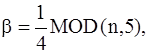
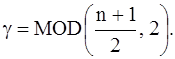
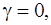 следовательно,
следовательно, 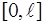 - период.
- период.
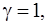 функция продолжается четным образом.
функция продолжается четным образом.
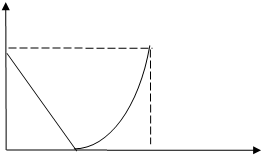



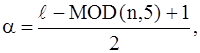
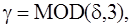


 функция продолжается четным образом.
функция продолжается четным образом.
 промежуток,
промежуток, 

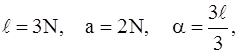
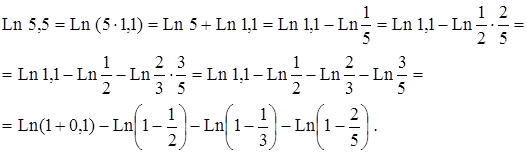
 , (2.1)
, (2.1)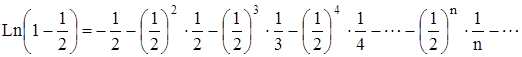 , (2.2)
, (2.2) , (2.3)
, (2.3)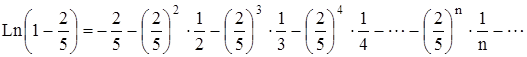 . (2.4)
. (2.4)
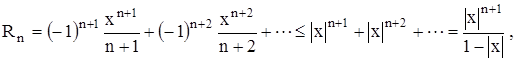
 (2.5)
(2.5)
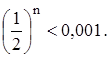





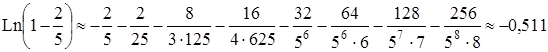 .
.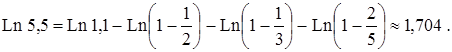
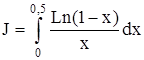 с точностью до 0,001.
с точностью до 0,001. то положим f(0) = -1.
то положим f(0) = -1.
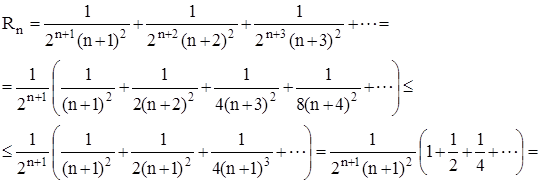
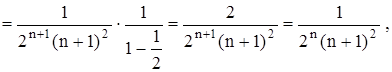
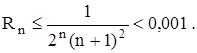
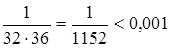 . Поэтому берем 5 слагаемых в разложении
. Поэтому берем 5 слагаемых в разложении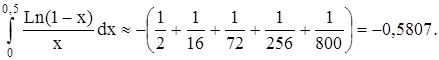
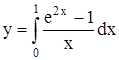 с точностью до 0,001.
с точностью до 0,001.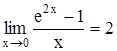 , то положим F(0) = 2.
, то положим F(0) = 2.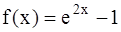 . Разложим f(x) в степенной ряд
. Разложим f(x) в степенной ряд
 - n-ый остаток, допускающий оценку Лагранжа.
- n-ый остаток, допускающий оценку Лагранжа. где
где 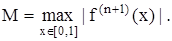
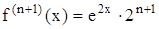 и экспонента достигает максимального значения на правом конце отрезка, то
и экспонента достигает максимального значения на правом конце отрезка, то  . Следовательно,
. Следовательно,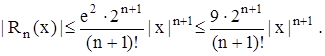
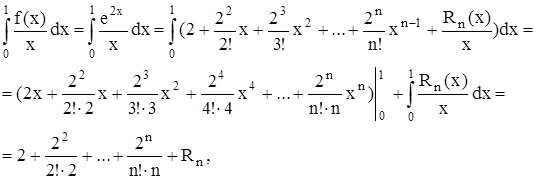
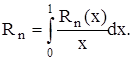
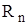 сверху:
сверху:
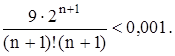
 и требуемая точность
и требуемая точность