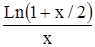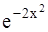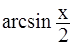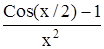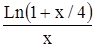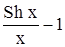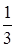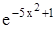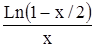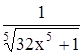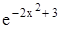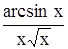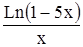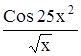Методические указания и индивидуальные задания
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
к модулю 12
Курск 2001
Составитель Е.В. Журавлева
УДК 517.1
Функциональные ряды: Метод. указания и индивидуальные задания к модулю 12 системы РИТМО /Курск. гос. техн. ун-т; Сост. Е.В. Журавлева. Курск. 2001. 30с.
Излагаются методические рекомендации по выполнению модуля 12, в том числе и с использованием программного продукта MATHCAD, приведены индивидуальные задания для студентов.
Предназначены для студентов технических специальностей.
Табл. 7. Библиогр.: 8 назв.
Рецензент зав. кафедрой высшей математики, к. т. н. Дроздов В.И.
Текст печатается в авторской редакции
ЛР № 020280 от 09.12.96. ПДЛ № 50 – 25 от 01.04.97. Подписано в печать................ Формат 60 х 84 1/16. Печать офсетная. Усл. печ. л. Уч.-изд.л. Тираж 100 экз. Заказ. Бесплатно. Курский государственный технический университет. Подразделение оперативной полиграфии Курского государственного технического университета. Адрес университета и подразделения оперативной полиграфии: 305040 Курск, ул. 50 лет Октября, 94.
Содержание
Введение ……………………………………..…………………………………… 4 1. Индивидуальные задания ………………………….………….…………….…4 1.1. Теоретические упражнения. …………………………….…………….. 4 1.2. Практические задания ……………………………………………….…..6 1.2.1. Задание 1 ………………………………………………………………6 1.2.2. Задание 2 ……………………………………………..………………..9 1.2.3. Задание 3 ……………………………………………………………..13 1.2.4. Задание 4 ……………………………………………………………..16 1.2.5. Задание 5. ………………………………………………...………….17 1.2.6. Задание 6. …………………………………………………………....19 1.2.7. Задание 7 …………………………………………………...………...22 2. Примеры выполнения заданий. ………………………………………….……26 2.1. Пример 1 ………………………………………...……………………….26 2.2. Пример 2. ………………………………………………...……………...28 2.3. Пример 3. …………………………………………………………...…...29 3. Контрольные вопросы. ………………………………………………..……….30 Библиографический список. ……………………………………………………...31
Введение
Данная работа предназначена для студентов, изучающих высшую математику и работающих в системе РИТМО, содержит теоретические упражнения, контрольные вопросы, расчетные задания и примеры выполнения заданий к модулю 12 «Функциональные ряды». Теоретический материал, необходимый для выполнения заданий, можно найти в книгах, указанных в библиографическом списке. При выполнении модуля каждый студент получает свой номер варианта n у преподавателя. Кроме параметра n в задании 7 используется параметр N – порядковый номер группы в потоке, а также используется функция MOD(n, q) – остаток от деления номера варианта n на заданное число q. При комплектации индивидуальных заданий для каждого варианта используется трехуровневая система. Каждый уровень предлагает студенту свой набор задач. Их решение требует удовлетворительного, хорошего и отличного знания материала соответственно. Каждый студент, в зависимости от степени своей подготовленности, должен: 1) выбрать определенный уровень; 2) выполнить задания этого уровня. Что необходимо сделать? Выполнить теоретическое упражнение и следующие практические задания: для первого уровня – решить задания 1,3,4,6; для второго уровня – решить задания 1,2,3,5,6; для третьего уровня – решить задания 1-7.
1. Индивидуальные задания
1.1. Теоретические упражнения
1. Дайте определение функционального ряда. Сформулируйте и докажите теорему об интегрировании функционального ряда. 2. Дайте определение функционального ряда. Сформулируйте и докажите теорему о дифференцировании функционального ряда. 3. Дайте определение степенного ряда. Сформулируйте теорему Абеля об области сходимости степенного ряда. 4. Докажите теорему Абеля об области сходимости степенного ряда. 5. Сформулируйте и докажите теорему об интервале сходимости степенного ряда. 6. Дайте определение радиуса сходимости степенного ряда. Укажите способ определения радиуса сходимости. Приведите формулу для вычисления радиуса сходимости с использованием признака Даламбера. 7. Дайте определение радиуса сходимости степенного ряда. Укажите способ определения радиуса сходимости. Приведите формулу для вычисления радиуса сходимости с использованием признака Коши. 8. Приведите формулу для ряда Тейлора. Сформулируйте и докажите условие, при котором этот ряд сходится и равен самой функции. 9. Сформулируйте и докажите теорему о дифференцировании степенного ряда. 10. Вывести формулу разложения в ряд функции y = ex. 11. Вывести формулу разложения в ряд функции y = sin x. 12. Вывести формулу разложения в ряд функции y = cos x. 13. Вывести формулу разложения в ряд (1 + x)m. 14. Вывести формулу разложения в ряд функции y = ln(1 + x). 15. Дайте определение тригонометрического ряда, ряда Фурье для функции f(x) на [-p, p], для функции f(x) на 16. Дайте определение тригонометрического ряда. Вывести коэффициенты Фурье для функции f(x) на [-p, p]. 17. Дайте определение тригонометрического ряда. Вывести коэффициенты Фурье для функции f(x) на 18. Дайте определение кусочно монотонной функции. Сформулируйте теорему о разложимости кусочно монотонной функции в ряд Фурье. 19. Дайте определение тригонометрического ряда. Приведите коэффициенты Фурье для четной и нечетной функции. 20. Сформулируйте и докажите теорему о сходимости ряда Фурье в данной точке. 21. Сформулируйте и докажите достаточное условие сходимости ряда Фурье.
1.2. Практические задания
1.2.1. Задание 1
Найти область сходимости функционального ряда Таблица 1.1 Индивидуальные задачи к заданию 1
Продолжение табл.1.1
Продолжение табл.1.1
Продолжение табл.1.1
Продолжение табл.1.1
1.2.2. Задание 2
Найти область сходимости функционального ряда Таблица 2.1 Индивидуальные задачи к заданию 2
Продолжение табл.1.2
Продолжение табл.1.2
Продолжение табл.1.2
Задание 3
Разложить функцию f(x) в ряд по степеням x – x0.
Таблица 1.3 Индивидуальные задачи к заданию 3
Продолжение табл.1.3
Продолжение табл.1.3
1.2.4. Задание 4
Вычислить значение функции f(x) в заданной точке x0 (f(x0)) с точностью до 0,001. Таблица 1.4 Индивидуальные задачи к заданию 4
Продолжение табл.1.4
1.2.5. Задание 5
Вычислить определенный интеграл Таблица 1.5 Индивидуальные задачи к заданию 5
Продолжение табл.1.5
Продолжение табл.1.5
|


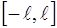 .
. .
.





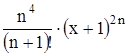
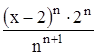

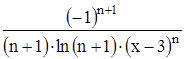



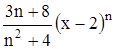




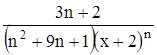
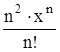



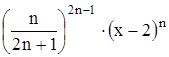



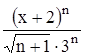








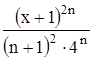


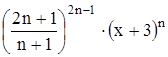













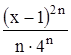

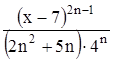


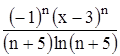


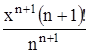









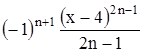
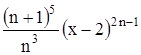

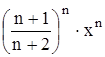
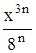



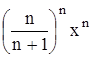








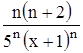










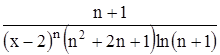
 .
.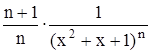



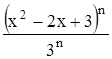
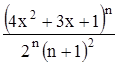











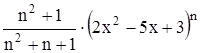

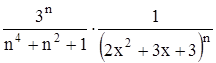
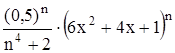


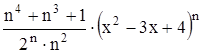
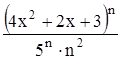

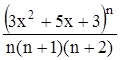

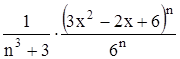






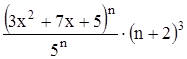







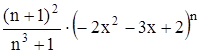
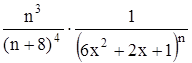







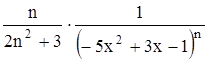
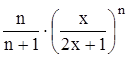

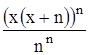


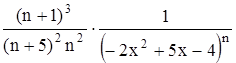


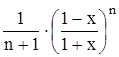






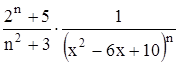



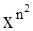




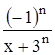




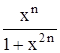



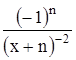
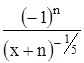
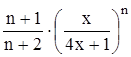






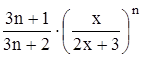

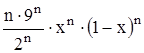
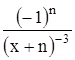







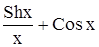



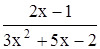




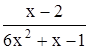
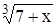

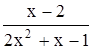




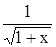








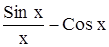














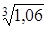
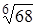

























 с точностью до 0,001.
с точностью до 0,001.