 В’язкість, або внутрішнє тертя, у газах зумовлена переміщенням молекул, що мають різні імпульси, між шарами газу, які рухаються з різними швидкостями. Наприклад, якщо потік газу контактує з безмеж-ною нерухомою площиною і рухаєть-ся паралельно до неї (рис. 7.2) то шари газу поблизу площини матимуть найменшу швидкість. З віддаленням від площини швидкість шарів зростатиме.
В’язкість, або внутрішнє тертя, у газах зумовлена переміщенням молекул, що мають різні імпульси, між шарами газу, які рухаються з різними швидкостями. Наприклад, якщо потік газу контактує з безмеж-ною нерухомою площиною і рухаєть-ся паралельно до неї (рис. 7.2) то шари газу поблизу площини матимуть найменшу швидкість. З віддаленням від площини швидкість шарів зростатиме.
Отже, між шарами виникає градієнт швидкості, спрямований перпендикулярно до напряму потоку. Обмін молекулами між шарами спричинює гальмування швидшого шару і пришвидшення повільного. В цьому полягає механізм виникнення внутрішнього тертя у газі. Величиною, що переноситься у цьому випадку, є імпульс молекули А=mv. За таких умов рівняння перенесення (7.5) набуває вигляду
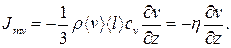 (7.12)
(7.12)
Це рівняння Ньютона для внутрішнього тертя. Тут  – коефіцієнт динамічної в’язкості газу.
– коефіцієнт динамічної в’язкості газу.
Подібно до коефіцієнта теплопровідності c коефіцієнт в’язкості газів h не залежить від тиску і збільшується з підвищенням температури (h ~  ). Поряд з коефіцієнтом динамічної в’язкості h на практиці використовують і коефіцієнт кінематичної в’язкості
). Поряд з коефіцієнтом динамічної в’язкості h на практиці використовують і коефіцієнт кінематичної в’язкості
 . (7.13)
. (7.13)
Подібність законів перенесення у газах (7.6), (7.11), (7.12) зумовлена спільним для цих явищ механізмом перемішування молекул газу внаслідок їхнього хаотичного руху і взаємодії. Якщо порівняти отримані вирази для коефіцієнтів перенесення, то неважко виявити взаємозв’язок між ними:
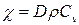 ,
, 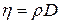 ,
,  . (7.14)
. (7.14)
Ми розглянули явища перенесення, коли градієнт величини А є сталим. Однак часто потрібно описати ці явища за умови, коли  . Наприклад, якщо ізольовану термодинамічну систему, що перебуває у нерівноважному стані, залишити саму на себе, то з часом вона перейде до рівноважного стану. За цих умов у середовищі відбувається вирівнювання температур або концентрацій газу в усіх просторових точках об’єму, в якому міститься газ. Це нестаціонарні явища перенесення, які описують дещо іншими співвідношеннями, ніж (7.6), (7.11), (7.12). Зокрема, рівняння нестаціонарної теплопровідності в ізотропному однорідному середовищі
. Наприклад, якщо ізольовану термодинамічну систему, що перебуває у нерівноважному стані, залишити саму на себе, то з часом вона перейде до рівноважного стану. За цих умов у середовищі відбувається вирівнювання температур або концентрацій газу в усіх просторових точках об’єму, в якому міститься газ. Це нестаціонарні явища перенесення, які описують дещо іншими співвідношеннями, ніж (7.6), (7.11), (7.12). Зокрема, рівняння нестаціонарної теплопровідності в ізотропному однорідному середовищі
 , (7.15)
, (7.15)
де 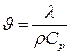 – температуропроводність середовища;
– температуропроводність середовища;  – оператор Лапласа.
– оператор Лапласа.
Рівняння нестаціонарної дифузії в ізотропному однорідному середовищі
 , (7.16)
, (7.16)
де Cp – питома теплоємність середовища за сталого тиску;  – оператор Лапласа.
– оператор Лапласа.

 В’язкість, або внутрішнє тертя, у газах зумовлена переміщенням молекул, що мають різні імпульси, між шарами газу, які рухаються з різними швидкостями. Наприклад, якщо потік газу контактує з безмеж-ною нерухомою площиною і рухаєть-ся паралельно до неї (рис. 7.2) то шари газу поблизу площини матимуть найменшу швидкість. З віддаленням від площини швидкість шарів зростатиме.
В’язкість, або внутрішнє тертя, у газах зумовлена переміщенням молекул, що мають різні імпульси, між шарами газу, які рухаються з різними швидкостями. Наприклад, якщо потік газу контактує з безмеж-ною нерухомою площиною і рухаєть-ся паралельно до неї (рис. 7.2) то шари газу поблизу площини матимуть найменшу швидкість. З віддаленням від площини швидкість шарів зростатиме.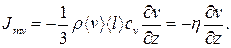 (7.12)
(7.12) – коефіцієнт динамічної в’язкості газу.
– коефіцієнт динамічної в’язкості газу. ). Поряд з коефіцієнтом динамічної в’язкості h на практиці використовують і коефіцієнт кінематичної в’язкості
). Поряд з коефіцієнтом динамічної в’язкості h на практиці використовують і коефіцієнт кінематичної в’язкості . (7.13)
. (7.13)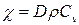 ,
, 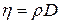 ,
,  . (7.14)
. (7.14) . Наприклад, якщо ізольовану термодинамічну систему, що перебуває у нерівноважному стані, залишити саму на себе, то з часом вона перейде до рівноважного стану. За цих умов у середовищі відбувається вирівнювання температур або концентрацій газу в усіх просторових точках об’єму, в якому міститься газ. Це нестаціонарні явища перенесення, які описують дещо іншими співвідношеннями, ніж (7.6), (7.11), (7.12). Зокрема, рівняння нестаціонарної теплопровідності в ізотропному однорідному середовищі
. Наприклад, якщо ізольовану термодинамічну систему, що перебуває у нерівноважному стані, залишити саму на себе, то з часом вона перейде до рівноважного стану. За цих умов у середовищі відбувається вирівнювання температур або концентрацій газу в усіх просторових точках об’єму, в якому міститься газ. Це нестаціонарні явища перенесення, які описують дещо іншими співвідношеннями, ніж (7.6), (7.11), (7.12). Зокрема, рівняння нестаціонарної теплопровідності в ізотропному однорідному середовищі , (7.15)
, (7.15)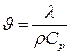 – температуропроводність середовища;
– температуропроводність середовища;  – оператор Лапласа.
– оператор Лапласа. , (7.16)
, (7.16)


