Процесс переноса энергии
Это процесс лежит в основе явления теплопроводности. Если в некоторой среде возникает градиент температуры, то возникает поток тепла. В этом случае переносимой вели-чиной будет средняя кинетическая энергия теплового дви-жения одной молекулы
Переносимую величину представим в виде:
где
Умножив и разделив на массу молекулы, и учтя, что
где
– коэффициент теплопроводности. Окончательно,
Полученное соотношение называется законом Фурье. Теплопроводность не зависит от давления и пропорцио-нальна Коэффициент теплопроводности может быть получен из коэффициентов диффузии и вязкости:
Коэффициент теплопроводности имеет размерность Общими свойствами всех трёх коэффициентов является то, что эмпирически определив
|

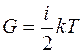 . Плотность потока тепла составит
. Плотность потока тепла составит . (2.14)
. (2.14) (2.15)
(2.15)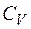 – молярная теплоемкость при постоянном объеме. Отсюда получаем
– молярная теплоемкость при постоянном объеме. Отсюда получаем . (2.16)
. (2.16)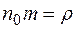 – плотность вещества и
– плотность вещества и  – удельная теплоемкость вещества, получаем выражение для теплового потока через единичную площадь:
– удельная теплоемкость вещества, получаем выражение для теплового потока через единичную площадь: (2.17)
(2.17) (2.18)
(2.18)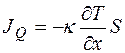 . (2.19)
. (2.19)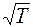 .
. . (2.20)
. (2.20) и численно равен энергии, переносимой в виде теплоты за 1 секунду через плоскую поверхность площадью
и численно равен энергии, переносимой в виде теплоты за 1 секунду через плоскую поверхность площадью 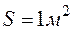 при градиенте температуры, равном единице.
при градиенте температуры, равном единице.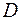 ,
, 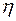 и
и  , мы можем вы-числить длину свободного пробега
, мы можем вы-числить длину свободного пробега 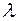 и эффективный диа-метр молекул
и эффективный диа-метр молекул  .
.


