ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ. Измерение коэффициента теплопроводности воздуха методом НАГРЕТОЙ НИТИ
Измерение коэффициента теплопроводности воздуха методом НАГРЕТОЙ НИТИ ЦЕЛЬ РАБОТЫ
Экспериментальное определение коэффициента тепло-проводности воздуха, находящегося вокруг нагретой элек-трическим током нити. В работе определяется электричес-кая мощность, выделяемая в нити и температура нити.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Тела, находящиеся при различных температурах, могут обмениваться внутренней энергией. Перенос энергии, теп-лообмен – это самопроизвольный, необратимый процесс распространения тепла в пространстве, обусловленный раз-ностью температур. Различаются три основных способа переноса тепла. 1. Теплопроводность – перенос, обусловленный взаимо-действием микрочастиц соприкасающихся тел, имеющих равную температуру. 2. Конвекция – перенос вследствие пространственного перемещения вещества. 3. Теплововое излучение – перенос посредством электро-магнитного поля с двойным взаимным превращением теп-лоты в энергию поля и наоборот. В реальных тепловых процессах, как правило, перенос тепла осуществляется одновременно тремя способами. В данной работе изучается первый из них. При отсутствии конвекции (макроскопического пере-мешивания теплых и холодных масс воздуха) перенос тепла происходит благодаря теплопроводности, связанной с теп-ловым движением молекул. Молекулы при этом обме-ниваются энергией, поэтому в основе теплопроводности ле-жит процесс переноса энергии. Поток тепла при этом оп-ределяется градиентом температуры:
где
При нагревании нити вдоль ра-диуса трубки создается градиент температуры. Площадь, через кото-рую передается тепло, равна пло-щади поверхности цилиндра, ко-аксиального с нагретой нитью. При этом поток тепла
где
Из (2.4.2) получим выражение для мощности теплого по-тока через внутреннюю цилиндрическую поверхность труб-ки радиуса
Полученное дифференциальное уравнение решим мето-дом разделения переменных:
Поскольку
Опыт проводится при постоянной температуре трубки, равной
Так как вблизи нити теплопроводность воздуха опреде-ляется температурой нити, то в (2.4.4) величина
Для определения производной необходимо знать зависи-мость Мощность теплового потока
где
Формула (2.4.5) позволяет по найденной эксперимен-тальной зависимости
|

 , (2.4.1)
, (2.4.1) – мощность, пересекающая воображаемую площадку
– мощность, пересекающая воображаемую площадку  , установленную перпендикулярно тепловому потоку;
, установленную перпендикулярно тепловому потоку; – координата, вдоль которой направлен градиент тем-пературы
– координата, вдоль которой направлен градиент тем-пературы 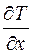 ;
; – коэффициент теплопроводности.
– коэффициент теплопроводности. Рассмотрим случай, когда поток тепла направлен от нагретой нити к стенкам внешней цилиндрической оболоч-ки (рис. 2.4.1)
Рассмотрим случай, когда поток тепла направлен от нагретой нити к стенкам внешней цилиндрической оболоч-ки (рис. 2.4.1) через любую промежуточную цилиндри-ческую оболочку радиуса
через любую промежуточную цилиндри-ческую оболочку радиуса  (
(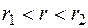 ) и площадью
) и площадью 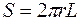 можно определить, пренебрегая утечками тепла через тор-цы цилиндра:
можно определить, пренебрегая утечками тепла через тор-цы цилиндра: , (2.4.2)
, (2.4.2)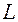 – длина цилиндра радиуса
– длина цилиндра радиуса 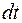 – интервал времени
– интервал времени . По определению, мощность теплого потока:
. По определению, мощность теплого потока: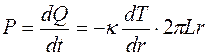 .
.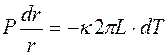 .
. , проинтегрируем левую часть от ра-диуса нити
, проинтегрируем левую часть от ра-диуса нити 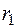 до радиуса трубки
до радиуса трубки 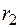 , а правую – от темпе-ратуры нити
, а правую – от темпе-ратуры нити 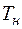 до температуры стенок трубки
до температуры стенок трубки  . С учетом знаков получим:
. С учетом знаков получим: ,
,  ,
, . (2.4.3)
. (2.4.3) . При этом увеличение электрической мощности, выделяемой в нити, на величину
. При этом увеличение электрической мощности, выделяемой в нити, на величину 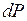 приводит к воз-растанию ее температуры на
приводит к воз-растанию ее температуры на  . Поэтому из (2.4.3) сле-дует
. Поэтому из (2.4.3) сле-дует . (2.4.4)
. (2.4.4) относится к температуре
относится к температуре  . При возрастании температуры нити на
. При возрастании температуры нити на  дополнительный перенос мощности на
дополнительный перенос мощности на 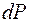 от нити к стенки трубки определяется только теплопровод-ностью слоя воздуха в близи нити. Из соотношения (2.4.4) получим
от нити к стенки трубки определяется только теплопровод-ностью слоя воздуха в близи нити. Из соотношения (2.4.4) получим (2.4.5)
(2.4.5) , которую находят по экспериментальным данным.
, которую находят по экспериментальным данным. находится по нап-ряжению
находится по нап-ряжению 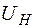 , измеренному на нити, и току
, измеренному на нити, и току 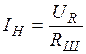 , теку-щему через образцовое сопротивление
, теку-щему через образцовое сопротивление 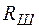 и нить. Для оп-ределения тока измеряется напряжение на образцовом со-противлении
и нить. Для оп-ределения тока измеряется напряжение на образцовом со-противлении 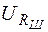 . Температура нити определяется из отно-шения
. Температура нити определяется из отно-шения
 , (2.4.6)
, (2.4.6) – сопротивление нити при
– сопротивление нити при 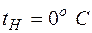 , Ом;
, Ом; – сопротивление нити при температуре опыта, Ом;
– сопротивление нити при температуре опыта, Ом;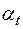 – температурный коэффициент сопротивления мате-риала нити,
– температурный коэффициент сопротивления мате-риала нити,  .
.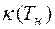 .
.


