Первый закон термодинамики и его применение к различным процессам
Эквивалентность количества теплоты и механической работы была установлена в середине XIX в. английским ученым Джоулем и немецким ученым Майером. Это привело к открытию одного из самых фундаментальных законов физики — закона сохранения энергии: энергия не возникает из ничего и не исчезает; в различных процессах она только превращается из одного вида в другой в эквивалентных количествах. Закон сохранения энергии в применении к тепловым процессам принято называть первым законом (или первым началом) термодинамики: внутренняя энергия системы может изменяться при совершении работы внешними силами над системой или в результате теплообмена:
1. Изобарный процесс. Работа газа.
При изобарном процессе количество теплоты, сообщаемое газу, расходуется как на его нагревание (т. е. на увеличение внутренней энергии), так и на работу расширения, которую газ совершает против сил внешнего давления. Поэтому первый закон термодинамики для изобарного процесса записывают в виде Q=A+DU. При изобарном нагревании газа на DT его объем увеличивается на DV. Работа газа при изобарном расширении может быть найдена как В результате для изобарного процесса можно записать:
Из этой записи следует, что молярная теплоемкость газа при постоянном давлении:
2. Изохорный процесс. Теорема Майера Так как в данном процессе объем газа не изменяется, то DV= 0, т.е. А = 0 - в изохорном процессе газ не совершает работы. Первый закон термодинамики принимает вид: Q = DU - в изохорном процессе вся сообщаемая газу теплота идет на увеличение его внутренней энергии. Для изохорного процесса можно записать:
Из этой записи следует, что молярная теплоемкость газа при постоянном объеме:
Теплоемкость газа зависит от вида процесса Молярная теплоемкость идеального газа при постоянном давлении или при постоянном объеме не зависит от его химического состава и температуры, а зависит только от числа степеней свободы молекул, которое в свою очередь зависит от числа атомов в этих молекулах. 3. Изотермический процесс Внутренняя энергия идеального газа зависит только от температуры, в данном же процессе температура не изменяется, следовательно, в изотермическом процессе U = const, т.е. DU = 0. Q = A, т е вся сообщенная газу теплота идет на совершение работы расширения газа. Изотермический процесс является наиболее энергетически выгодным для превращения внутренней энергии газа в механическую работу. 4. Адиабатный процесс Адиабатным называют процесс, происходящий без теплообмена системы с окружающей средой, т. е. при этом процессе Q = 0. Идеальным случаем осуществления адиабатного процесса явилась бы полная тепловая изоляция системы от окружающих тел (приблизительно такую теплоизоляцию создает сосуд Дюара или термос). В реальных условиях адиабатным можно считать быстропротекающий процесс, поскольку в данном случае теплообмен не успевает произойти.
Работа при адиабатном изменении объема газа может быть определена графическим способом. При одинаковом изменении объема газа в изотермическом процессе совершается работа большая, чем в адиабатном. Происходит это потому, что в адиабатном процессе давление зависит и от объема и от температуры газа, а в изотермическом — только от его объема (это приводит к тому, что при одинаковом изменении объема газа давление в адиабатном процессе изменяется быстрее, чем в изотермическом).
|

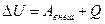 или количество теплоты, полученное системой, в общем случае расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил:
или количество теплоты, полученное системой, в общем случае расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил: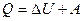 .
. Пусть в цилиндре с незакрепленным невесомым поршнем находится идеальный газ (рис.). Нагреем его, сообщив газу количество теплоты Q. Поскольку поршень не закреплен, давление газа р постоянно и равно атмосферному. При нагревании на DT происходит изобарное расширение газа и его объем увеличивается на DV = SDh (где S - площадь поршня, Dh - высота поднятия поршня). Работа расширения газа А = FDh = pSDh = рDV.
Пусть в цилиндре с незакрепленным невесомым поршнем находится идеальный газ (рис.). Нагреем его, сообщив газу количество теплоты Q. Поскольку поршень не закреплен, давление газа р постоянно и равно атмосферному. При нагревании на DT происходит изобарное расширение газа и его объем увеличивается на DV = SDh (где S - площадь поршня, Dh - высота поднятия поршня). Работа расширения газа А = FDh = pSDh = рDV.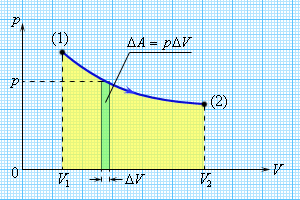 Эта формула для работы газа справедлива не только для изобарного процесса, но и для любого процесса, в котором объем газа изменяется на сколь угодно малую величину DV.
Эта формула для работы газа справедлива не только для изобарного процесса, но и для любого процесса, в котором объем газа изменяется на сколь угодно малую величину DV.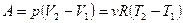 . В любом другом процессе работа газа может быть найдена как площадь под графиком процесса в р, V координатах. Из формулы для работы газа следует, что газовая постоянная численно равна работе которую совершает 1 моль идеального газа при изобарном нагревании на 1 К.
. В любом другом процессе работа газа может быть найдена как площадь под графиком процесса в р, V координатах. Из формулы для работы газа следует, что газовая постоянная численно равна работе которую совершает 1 моль идеального газа при изобарном нагревании на 1 К. .
.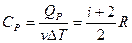 .
.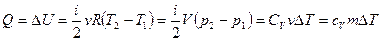 .
.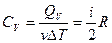 .
.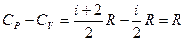 - теорема Майера (в честь немецкого врача, который одним из первых сформулировал закон сохранения и превращения энергии применительно к тепловым процессам): молярная теплоемкость идеального газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной.
- теорема Майера (в честь немецкого врача, который одним из первых сформулировал закон сохранения и превращения энергии применительно к тепловым процессам): молярная теплоемкость идеального газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной. Поскольку в адиабатном процессе Q = 0, то А = -DU, т. е. работа изменения объема газа происходит в адиабатном процессе за счет изменения внутренней энергии системы. При адиабатном расширении газ охлаждается, а при адиабатном сжатии — нагревается.
Поскольку в адиабатном процессе Q = 0, то А = -DU, т. е. работа изменения объема газа происходит в адиабатном процессе за счет изменения внутренней энергии системы. При адиабатном расширении газ охлаждается, а при адиабатном сжатии — нагревается.


