Практическое занятие по теме «Анализ интенсивности
экономического развития, его тенденции, закономерности»
Исследование интенсивности динамических процессов производится путем анализа уровней ряда динамики. Ряд динамики – ряд числовых значений определенного статистического показателя в последовательные моменты времени или периоды времени. Составляющими ряда динамики являются признак времени t (момент или интервал) и числовые значения показателя – уровни Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться относительными, абсолютными или средними величинами. Существуют различные виды рядов динамики. Их можно классифицировать по следующим признакам. 1) В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. 2) В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину за определенные интервалы времени (например, за сутки, месяц; год и т. п.), различают соответственно моментные и интервальные ряды динамики. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени (число рабочих на начало месяца, поставки сырья по периоду). Особенностью моментного ряда динамики является то, что, как правило, он отражает состояние фактического производства. Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Посредством таких рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды. Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов. Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, и поэтому их можно суммировать как не содержащие повторного счета. Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета 3) В зависимости от расстояния между уровнями ряды динамики подразделяются на ряды динамики с равноотстоящими уровнями и неравноотстоящими уровнями во времени. Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими. 4) В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные. Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. Для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют абсолютные и относительные показатели изменения ряда динамики: абсолютные приросты, абсолютное значение одного процента прироста, темпы роста и прироста. Рассматривая данные показатели, необходимо правильно выбирать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня с предыдущим получают цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) - базовые показатели. Абсолютный прирост (
где
Темп роста (
Темп прироста (
Темп прироста может быть вычислен также путем вычитания из темпов роста 100 %: Показатель абсолютного значения одного процента прироста (/%/) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах:
Расчет этого показателя имеет смысл только на цепной основе. Средние показатели рядов динамики являются обобщающей характеристикой их абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста. Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных. В интервальном ряду динамики с равноотстоящими уровнями во времени расчет среднего уровня ряда (
Для интервального ряда динамики с неравноотстоящими уровнями средний уровень ряда вычисляется по формуле:
где t - число периодов времени, в течение которых уровень не изменяется. Для моментного ряда с равноотстоящими уровнями средний уровень ряда рассчитывается по формуле средней хронологической:
где n – число уровней ряда. Средний уровень моментного ряда с разноотстоящими (неравноотстоящими) уровнями вычисляется по следующей формуле:
Средний абсолютный прирост – показатель, характеризующий среднюю абсолютную скорость роста (снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.д.). Определение среднего абсолютного прироста производится по формуле:
Средний темп роста – относительный показатель, выраженный в форме коэффициента и показывающий, во сколько раз увеличился уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежеквартально и т.п.). Среднегодовой темп роста вычисляется по формуле средней геометрической:
где m – число коэффициентов роста. Средний темп прироста – относительный показатель, выраженный в процентах и показывающий, на сколько увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.). Среднегодовой темп прироста получаем, вычтя из среднего темпа роста 100 %:
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития. Основная тенденция (тренд) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. Для определения основной тенденции развития ряда динамики применяется метод аналитического выравнивания. Суть его состоит в том, что основную тенденцию развития можно представить в виде математической функции: уравнение прямой, параболы второго порядка, степенной функции, гиперболы и др. Параметры уравнения определяются методом наименьших квадратов. Для уравнения прямой
Параметры уравнения определяются путем решения системы нормальных уравнений или по формулам: a 1= a 0 Для определения параметров уравнения прямой строится расчетная таблица:
Таблица – Расчет показателей для определения уравнения прямой линии
Если нумерация лет производится так, чтобы
Кроме того, для изучения тенденции развития возможно исследование цепных абсолютных приростов и коэффициентов роста. При этом расчетные формулы имеют следующий вид:
Иногда для уравнения тренда подходит одновременно несколько функций. Отбор наилучшей функции производится по величине остаточной дисперсии (отклонения теоретических уровней от эмпирических), которая вычисляется по формуле:
Построенные трендовые модели можно использовать для прогнозирования. Осуществляя прогноз, важно давать не только точечную оценку, но и интервальную с учетом погрешности прогноза. Погрешность может быть представлена в виде доверительного интервала.
где
t – значение статистики Стьюдента (р =0,05; р =0,01). Если t – период упреждения (прогноза) будет равен t = i + 1, то доверительный интервал прогноза будет иметь вид:
где Среднее квадратическое отклонение прогноза вычисляется по формуле:
где n – число наблюдений; t 1 – период времени, для которого производится прогноз (период упреждения), t 1 = n + 1;
Так как время нумеруется (t = 1, 2,... n), то
|

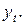
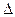 ) измеряет абсолютную скорость роста (или снижения) уровня ряда за единицу времени (месяц, квартал, год и т.д.). Он показывает, на сколько единиц увеличивается или уменьшается уровень по сравнению с базисным, т.е. за тот или иной промежуток времени. Его величина определяется как разность двух сравниваемых уровней:
) измеряет абсолютную скорость роста (или снижения) уровня ряда за единицу времени (месяц, квартал, год и т.д.). Он показывает, на сколько единиц увеличивается или уменьшается уровень по сравнению с базисным, т.е. за тот или иной промежуток времени. Его величина определяется как разность двух сравниваемых уровней: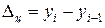 или
или  ,
,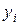 - уровень i -го года;
- уровень i -го года;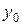 - уровень базисного года.
- уровень базисного года. ) – относительный показатель, характеризующий интенсивность процесса роста (снижения). Он показывает, сколько процентов составляет уровень данного периода по сравнению с базисным или предыдущим уровнем, т.е. характеризует относительную скорость изменения уровня ряда в единицу времени. Он вычисляется по формуле:
) – относительный показатель, характеризующий интенсивность процесса роста (снижения). Он показывает, сколько процентов составляет уровень данного периода по сравнению с базисным или предыдущим уровнем, т.е. характеризует относительную скорость изменения уровня ряда в единицу времени. Он вычисляется по формуле: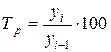 или
или  .
.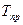 ) – относительный показатель, характеризующий величину прироста (снижения) и рассчитываемый как отношение абсолютного прироста к предыдущему или базисному уровню:
) – относительный показатель, характеризующий величину прироста (снижения) и рассчитываемый как отношение абсолютного прироста к предыдущему или базисному уровню: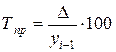 или
или 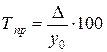 .
.
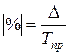 или
или 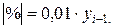
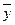 ) производится по формуле средней арифметической простой:
) производится по формуле средней арифметической простой: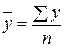 .
.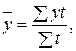
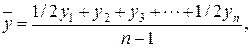
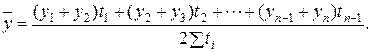
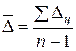 или
или 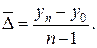
 , или
, или 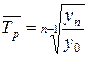 ,
,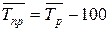 .
.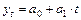 система нормальных уравнений имеет вид:
система нормальных уравнений имеет вид: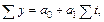
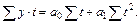
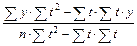 ;
;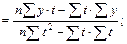
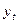
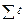 =0, то параметры уравнения определяются по формулам:
=0, то параметры уравнения определяются по формулам: ;
;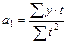 .
.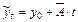 ;
; .
.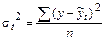 .
.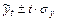 ,
, – среднее квадратическое отклонение ошибки тренда;
– среднее квадратическое отклонение ошибки тренда;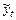 – теоретические значения уровней ряда;
– теоретические значения уровней ряда; ,
,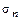 – среднее квадратическое отклонение прогноза.
– среднее квадратическое отклонение прогноза.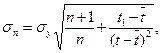
 – значение порядкового номера уровня, стоящего в середине ряда динамики.
– значение порядкового номера уровня, стоящего в середине ряда динамики.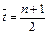 .
.


