Будем раскрашивать вершины графа. Раскраска графа называется правильной, если смежные вершины окрашены в разные цвета.
Минимальное количество цветов, при котором получается. правильная раскраска  называется хроматическим числом графа
называется хроматическим числом графа  и обозначается
и обозначается  . Через
. Через 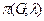 будет обозначаться число всех различных правильных раскрасок
будет обозначаться число всех различных правильных раскрасок  с помощью
с помощью  красок. Очевидно, хроматическое число равно минимальному из тех
красок. Очевидно, хроматическое число равно минимальному из тех  , для которых
, для которых 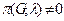 .
.
Напомним, что суграфом или остовом графа называется часть графа, включающая все его  вершин. Следующая формула для вычисления
вершин. Следующая формула для вычисления 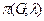 доказывается непростыми комбинаторными рассуждениями.
доказывается непростыми комбинаторными рассуждениями.
Теорема. Справедлива формула 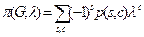 , где
, где 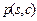 — число суграфов,
— число суграфов,  — ребер и
— ребер и  — компонент связности (если для
— компонент связности (если для  и
и  таких суграфов нет, полагаем
таких суграфов нет, полагаем 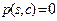 ).
).
Будем рассматривать 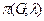 как функцию переменной
как функцию переменной  . Очевидны следующие свойства
. Очевидны следующие свойства 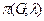 :
:
1) 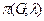 - многочлен степени
- многочлен степени  со старшим коэффициентом, равным 1 (так как наибольшее число компонент связности имеет суграф, состоящий из одних вершин графа; для этого суграфа
со старшим коэффициентом, равным 1 (так как наибольшее число компонент связности имеет суграф, состоящий из одних вершин графа; для этого суграфа  ).
).
2) свободный член у 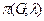 равен 0.
равен 0.
Данную формулу можно использовать для непосредственного вычисления 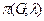 в простых случаях.
в простых случаях.
 Пример. Вычислим
Пример. Вычислим  для «треугольника»
для «треугольника» 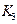 :
:
Ясно, что у 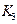 имеется:
имеется:
a) один суграф без ребер ( );
);
b) три суграфа с одним ребром ( );
);
c) три суграфа с двумя ребрами ( );
);
d) один суграф с тремя ребрами ( ).
).
Поэтому числа 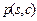 для этого графа таковы:
для этого графа таковы:
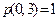 ,
,  ,
,  ,
,  .
.
Согласно формуле для 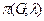
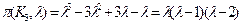 .
.
Из последней формулы следует, что хроматическое число 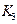 равно 3, что, конечно, легко доказать непосредственно.
равно 3, что, конечно, легко доказать непосредственно.
Следующие леммы позволяют свести подсчет функции 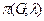 к подсчету ее для более простых графов.
к подсчету ее для более простых графов.
 Лемма 1. Если граф
Лемма 1. Если граф  состоит из двух несвязных частей
состоит из двух несвязных частей 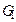 и
и  , то справедлива формула
, то справедлива формула
 .
.
Доказательство следует из очевидного факта, что раскраски  и
и  можно выбирать независимо.
можно выбирать независимо.
 Лемма 2. Если граф
Лемма 2. Если граф  получен из двух графов
получен из двух графов  и
и  склеиванием по одной вершине, то
склеиванием по одной вершине, то
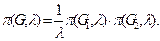
Доказательство.  Зафиксировав раскраску
Зафиксировав раскраску  (одну из возможных
(одну из возможных 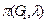 ), получим, что
), получим, что  допускает раскраску, при которой вершина
допускает раскраску, при которой вершина 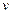 имеет определенный цвет. Такие раскраски
имеет определенный цвет. Такие раскраски  составляют
составляют 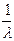 часть всех раскрасок из
часть всех раскрасок из 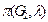 возможных. Как следствие получаем требуемый результат.
возможных. Как следствие получаем требуемый результат. 
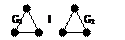 Лемма 3. Если граф
Лемма 3. Если граф  получен из двух графов
получен из двух графов 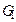 и
и  с помощью ребра
с помощью ребра  , то
, то

 .
.
Доказательство аналогично доказательству леммы 2.  Зафиксировав одну из
Зафиксировав одну из 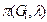 раскрасок
раскрасок 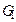 , получим, что
, получим, что  допускает те раскраски, при которых вершина
допускает те раскраски, при которых вершина 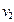 окрашена в любой цвет; кроме цвета вершины
окрашена в любой цвет; кроме цвета вершины  . Таких цветов
. Таких цветов  , а раскрасок
, а раскрасок  .
. 
Лемма 4. (Предложена студентом группы ФММ 01 М. Бузуверовым). Если граф  получен из двух графов
получен из двух графов 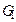 и
и  склеиванием по ребру
склеиванием по ребру  , то
, то
 .
.
Доказательство.  Зафиксировав раскраску
Зафиксировав раскраску 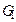 (одну из возможных
(одну из возможных 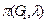 ), получим, что
), получим, что  допускает раскраску, при которой вершины
допускает раскраску, при которой вершины  и
и 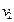 имеют определенный цвет. Такие раскраски
имеют определенный цвет. Такие раскраски  составляют
составляют  часть всех раскрасок из
часть всех раскрасок из 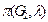 возможных. Как следствие получаем требуемый результат.
возможных. Как следствие получаем требуемый результат. 
Лемма 5. Пусть граф  получен из графа
получен из графа 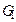 добавлением ребра
добавлением ребра  без изменения числа вершин. Обозначим через
без изменения числа вершин. Обозначим через 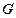 граф, полученный из
граф, полученный из  склеиванием вершин, инцидентных ребру
склеиванием вершин, инцидентных ребру  , и последующим отождествлением кратных ребер. Тогда
, и последующим отождествлением кратных ребер. Тогда
 .
.

Доказательство.  Очевидно, что
Очевидно, что 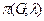 равно
равно 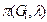 минус число раскрасок
минус число раскрасок  , в которых концы ребра
, в которых концы ребра  одинаково раскрашены. Но последнее и есть
одинаково раскрашены. Но последнее и есть  .
. 
Примеры.
1).  — полный граф с
— полный граф с  вершинами (случай
вершинами (случай 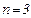 уже был рассмотрен). Выражение для
уже был рассмотрен). Выражение для 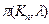 можно получить из общих свойств многочлена
можно получить из общих свойств многочлена 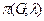 . Так как в
. Так как в  каждая вершина соединена со всеми остальными вершинами ребрами,
каждая вершина соединена со всеми остальными вершинами ребрами,  нельзя раскрасить менее, чем
нельзя раскрасить менее, чем  красками. Значит,
красками. Значит, 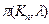 - многочлен
- многочлен  -й степени со свободным членом, равным 0, обращающийся в 0 при
-й степени со свободным членом, равным 0, обращающийся в 0 при  , и со старшим коэффициентом 1. Отсюда следует, что
, и со старшим коэффициентом 1. Отсюда следует, что
 .
.
2).  — дерево с
— дерево с  вершинами. Удалим из дерева какое-нибудь концевое ребро. При применении леммы 5 заметим, что граф
вершинами. Удалим из дерева какое-нибудь концевое ребро. При применении леммы 5 заметим, что граф  в этом случае есть дерево с
в этом случае есть дерево с  вершиной
вершиной  , а
, а 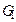 состоит из
состоит из  и изолированной вершины. Тогда по лемме 5 с учетом леммы 1 получим:
и изолированной вершины. Тогда по лемме 5 с учетом леммы 1 получим:
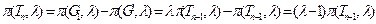 .
.
Заметив, что 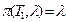 (так как
(так как 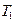 — изолированная вершина), получим по индукции:
— изолированная вершина), получим по индукции:
 .
.
3).  — цикл с
— цикл с  вершинами. Для вычисления
вершинами. Для вычисления 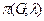 применим лемму 5. Удалив из
применим лемму 5. Удалив из  одно ребро, получим
одно ребро, получим 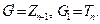 Тогда
Тогда
 .
.
Аналогично получим цепочку равенств:
 ,
,
..............
 ,
,
Умножив каждое равенство для 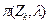 на
на  и сложив их, получим после сокращения
и сложив их, получим после сокращения 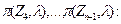
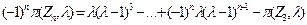
Воспользовавшись формулой для суммы геометрической прогрессии и тем, что
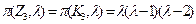 ,
,
получим:
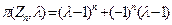 .
.
Итак, для  — полного графа с
— полного графа с  вершинами
вершинами
 ; (1)
; (1)
для  — дерева с
— дерева с  вершинами
вершинами
 ; (2)
; (2)
для  — цикла с
— цикла с  вершинами
вершинами
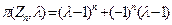 . (3)
. (3)
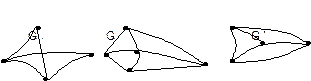
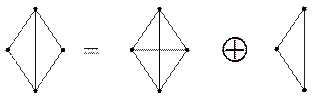
При нахождении хроматического полинома удобно использовать символическое графическое изображение. Например, вместо записи  , где графы имеют вид
, где графы имеют вид
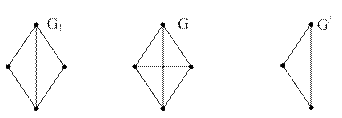
удобно представить это уравнение рисунком.
Задачи
Пример 1. Дан граф  .
.
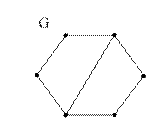
Постройте хроматический полином  графа
графа  и определите его хроматическое число
и определите его хроматическое число  .
.
Решение.
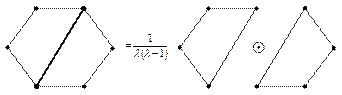

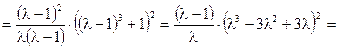
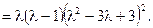
Так как  , а
, а  , то
, то  .
.
Ответ. 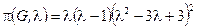 ,
,  .
.
Обратите внимание, что окончательная запись хроматического полинома должна иметь вид
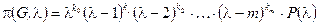 , где
, где  не имеет действительных корней. В этом случае
не имеет действительных корней. В этом случае  .
.
Пример 2. Дан граф  .
.
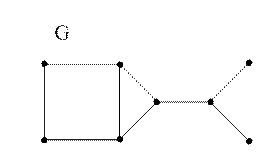
Постройте хроматический полином  графа
графа  и определите его хроматическое число
и определите его хроматическое число  .
.
Решение. 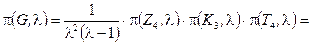
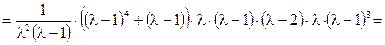
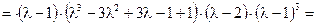
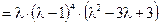 . См. рисунок.
. См. рисунок.
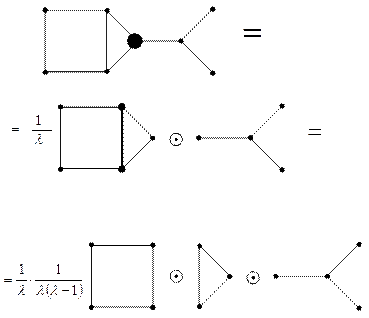
Так как  , а
, а 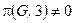 , то
, то 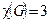 .
.
Ответ.  ,
,  .
.

 называется хроматическим числом графа
называется хроматическим числом графа  . Через
. Через 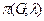 будет обозначаться число всех различных правильных раскрасок
будет обозначаться число всех различных правильных раскрасок  красок. Очевидно, хроматическое число равно минимальному из тех
красок. Очевидно, хроматическое число равно минимальному из тех 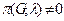 .
. вершин. Следующая формула для вычисления
вершин. Следующая формула для вычисления 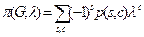 , где
, где 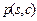 — число суграфов,
— число суграфов,  — ребер и
— ребер и  — компонент связности (если для
— компонент связности (если для 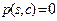 ).
). ).
). Пример. Вычислим
Пример. Вычислим  для «треугольника»
для «треугольника» 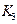 :
: );
); );
); );
); ).
).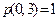 ,
,  ,
,  ,
,  .
.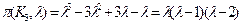 .
. Лемма 1. Если граф
Лемма 1. Если граф 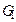 и
и  , то справедлива формула
, то справедлива формула .
. Лемма 2. Если граф
Лемма 2. Если граф 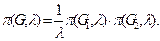
 Зафиксировав раскраску
Зафиксировав раскраску 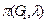 ), получим, что
), получим, что 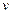 имеет определенный цвет. Такие раскраски
имеет определенный цвет. Такие раскраски 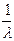 часть всех раскрасок из
часть всех раскрасок из 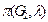 возможных. Как следствие получаем требуемый результат.
возможных. Как следствие получаем требуемый результат. 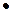
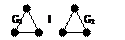 Лемма 3. Если граф
Лемма 3. Если граф  , то
, то
 .
.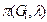 раскрасок
раскрасок 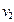 окрашена в любой цвет; кроме цвета вершины
окрашена в любой цвет; кроме цвета вершины  . Таких цветов
. Таких цветов  , а раскрасок
, а раскрасок  .
.  .
.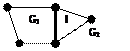
 и
и 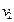 имеют определенный цвет. Такие раскраски
имеют определенный цвет. Такие раскраски  часть всех раскрасок из
часть всех раскрасок из 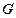 граф, полученный из
граф, полученный из  .
.

 .
.  — полный граф с
— полный граф с  уже был рассмотрен). Выражение для
уже был рассмотрен). Выражение для 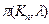 можно получить из общих свойств многочлена
можно получить из общих свойств многочлена  каждая вершина соединена со всеми остальными вершинами ребрами,
каждая вершина соединена со всеми остальными вершинами ребрами,  , и со старшим коэффициентом 1. Отсюда следует, что
, и со старшим коэффициентом 1. Отсюда следует, что .
. — дерево с
— дерево с  в этом случае есть дерево с
в этом случае есть дерево с  вершиной
вершиной  , а
, а 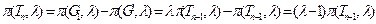 .
.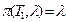 (так как
(так как 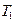 — изолированная вершина), получим по индукции:
— изолированная вершина), получим по индукции: .
. — цикл с
— цикл с 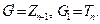 Тогда
Тогда .
. ,
, ,
,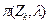 на
на  и сложив их, получим после сокращения
и сложив их, получим после сокращения 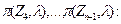
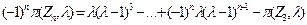
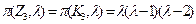 ,
,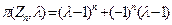 .
. — полного графа с
— полного графа с  — дерева с
— дерева с  — цикла с
— цикла с  , где графы имеют вид
, где графы имеют вид

 .
.
 графа
графа 

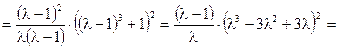
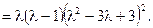
 , а
, а  , то
, то  .
.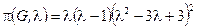 ,
, 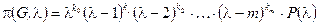 , где
, где  не имеет действительных корней. В этом случае
не имеет действительных корней. В этом случае  .
.
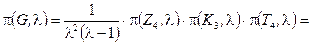
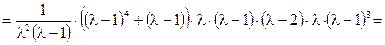
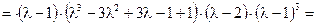
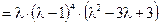 . См. рисунок.
. См. рисунок.
 , а
, а 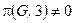 , то
, то 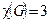 .
. ,
, 


