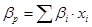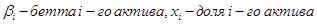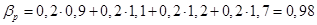Задача 5. Акция АА имеет ожидаемую доходность 12% и среднее квадратическое отклонение (риск) 7%
Акция АА имеет ожидаемую доходность 12% и среднее квадратическое отклонение (риск) 7%. Соответствующие значения этих показателей для акции ВВ – 18 и 30%. Коэффициент корреляции между ожидаемыми доходностями акций составляет 0,7. 1. Рассчитайте ожидаемую доходность и среднее квадратическое отклонение портфеля, состоящего на 35% из АА и на 65% из ВВ. 2. Влияет ли изменение структуры портфеля на его характеристики? 3. Не делая вычислений, ответьте на вопрос, как изменятся характеристики портфеля если: а) повысится доля акций АА. Б) повысится доля акций ВВ. 4. Сделайте соответствующие расчеты для двух случаев: а) доля акций АА увеличена на 10 процентных пунктов. Б) доля акций ВВ увеличена на 15 процентных пунктов. 5. Влияет ли знак коэффициента корреляции на характеристики а) отдельных бумаг б) портфеля 6. Не делая вычислений, ответьте на вопрос, изменятся ли характеристики портфеля, если в условиях задачи коэффициент корреляции отрицателен? 7. Рассчитайте значения характеристик портфеля, если коэффициент корреляции равен а) 0, б) -0,6.
1) По аналоги с прошлой задачей:
Так как сигмы, и коэффициент корреляции уже даны, находим риск портфеля сразу, а не через ту жопа, как в предыдущей задаче:
2) Для проверки достаточно изменить соотношение долей акций. Предположим изменение до наоборот: 65% - акций АА и 35% ВВ.
3) Если повысится доля акций АА, то доходность портфеля упадет, и рисковость снизится. Если же увеличится доля ВВ, все произойдет наоборот. 4) А)
5) Что за н….уй? Конечно влияет. Правда влияет он только на риск. И только на риск портфеля. Отрицательный знак понижает рисковость портфеля. Следовательно – в портфеле с двумя типами акций, изменяющих свою доходность разнонаправленно риск меньше! 6) ДААА! Рисковость портфеля упадет! Так как произойдет диверсификация активом, когда при падении доходности одного, доходность другого возрастает – это нам как раз сообщает отрицательный знак. 7) Все и так понятно. Подсавим в формулу 1) и будет счастье.
Задача 6 Портфель инвестора состоит из ценных бумаг со следующими характеристиками:
Доходность без рисковых ценных бумаг равна 7%. Доходность на рынке в среднем 14% Рассчитайте: а) бетта портфеля. Б) доходность портфеля.
Решение: Будем считать, что структура капитала предполагает распределение всех активов в равных долях. Найдем бетта портфеля:
где
Доходность портфеля определяется по следующей формуле:
|

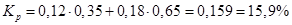 - ДОХОДНОСТЬ ПОРТФЕЛЯ.
- ДОХОДНОСТЬ ПОРТФЕЛЯ.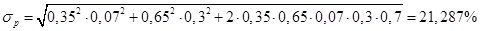 - РИСК ПОРТФЕЛЯ
- РИСК ПОРТФЕЛЯ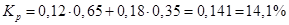 - таким образом и ежу понято, что изменение в структуре портфеля приведет и к изменению его характеристик.
- таким образом и ежу понято, что изменение в структуре портфеля приведет и к изменению его характеристик.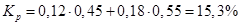 - снизилась
- снизилась риск также снизился. В случае б произойдет увеличение обоих параметров.
риск также снизился. В случае б произойдет увеличение обоих параметров.