Спектральный анализ сигналов на линиях связи.
Любая периодическая функция f(t) может быть представлена в виде суммы синусов (так называемый тригонометрический ряд Фурье):
По существу говоря, члены ряда Фурье - это гармоники или, с геометрической точки зрения, различные синусоиды, суммируя которые, можно с любой степенью точности представить любую периодическую функцию, а значит и любой периодический сигнал. Значит любой сигнал можно представить как сумму синусоид с разными частотами и амплитудами. Каждая составляющая синусоида называется также гармоникой, а набор всех гармоник называют спектральным разложением исходного сигнала или просто спектром сигнала. Практически в любом справочнике по высшей математике можно найти таблицы с разложениями в тригонометрические ряды Фурье простых сигналов. Число гармоник в разложении бесконечно большое, однако часто их можно ограничить конечным числом. Рассмотрим в качестве примера сигнал прямоугольной формы и его представление в виде суммы первых трех гармоник (рис ….). Эта функция раскладывается в ряд:
Как видно, ряд Фурье для этой функции состоит лишь из нечетных гармоник. На рисунке показано представление прямоугольных импульсов в виде суммы 1-й, 3-й и 5-й гармоник. Первая гармоника соответствует синусу с частотой w, третья 3w и т.д.
Полученные гармоники можно для наглядности представить в виде графика. (Необходимо обратить внимание, что по оси Х откладывается не время, а частота –F.)
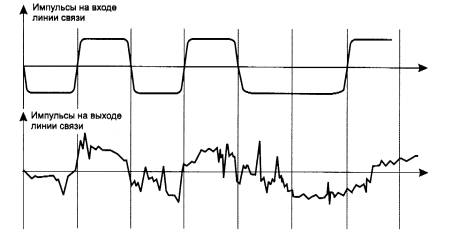
Дальнейшее рассмотрение будем проводить, принимая во внимание, что гармонические составляющие сигнала (гармоники) будут искажаться передающим каналом по-разному, т.е. спектр сигнала на входе в канал будет отличаться от спектра на его выходе. Искажение передающим каналом синусоиды какой-либо частоты приводит в конечном счете к искажению передаваемого сигнала любой формы, особенно если синусоиды различных частот искажаются неодинаково. Если это аналоговый сигнал, передающий речь, то изменяется тембр голоса за счет искажения обертонов – боковых частот. При передаче импульсных сигналов, характерных для компьютерных сетей, искажаются низкочастотные и высокочастотные гармоники, в результате фронты импульсов теряют свою прямоугольную форму (рис. ….). Вследствие этого на приемном конце линии сигналы могут плохо распознаваться
Рисунок 3‑1 Искажение импульсов в линии связи Линия связи искажает передаваемые сигналы из-за того, что ее физические параметры отличаются от идеальных. Так, например, медные провода всегда представляют собой некоторую распределенную по длине комбинацию активного сопротивления, емкостной и индуктивной нагрузки (рис. …). В результате для синусоид различных частот линия будет обладать различным полным сопротивлением, а значит, и передаваться они будут по-разному. Волоконно-оптический кабель также имеет отклонения, мешающие идеальному распространению света. Если линия связи включает промежуточную аппаратуру, то она также может вносить дополнительные искажения, так как невозможно создать устройства, которые бы одинаково хорошо передавали весь спектр синусоид, от нуля до бесконечности.
Рисунок 3‑2 Представление линии как распределенной индуктивно-емкостной нагрузки Кроме искажений сигналов, вносимых внутренними физическими параметрами линии связи, существуют и внешние помехи, которые вносят свой вклад в искажение формы сигналов на выходе линии. Поэтому сигналы на выходе линии связи обычно имеют сложную форму, как это и показано на рис. ….
|


 Ansin(wnt)
Ansin(wnt)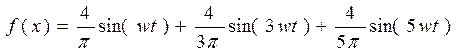 + …
+ …