Понятие и измерители риска финансовых активов
Тема 5. Риск и доходность портфеля финансовых активов
1. Понятие и измерители риска финансовых активов. 2. Бета - коэффициент как измеритель рыночного риска ценных бумаг. 3. Модельоценки доходности финансовых активов (CAPM).
Понятие и измерители риска финансовых активов
Диверсификация может осуществляться не только в отношении продуктов или направлений деятельности предприятия. Большое значение в финансовом менеджменте имеет диверсификация вложений в финансовые активы. Обычно инвесторы работают не с отдельными активами, а с некоторым набором активов, получившим название инвестиционного портфеля или портфеля ценных бумаг. Объединение акций в портфель приводит к снижению риска, поскольку цены различных акций изменяются неодинаково и потери по одним акциям могут компенсироваться получением дохода по другим. Если инвестор владеет портфелем, состоящим из множества различных акций, на первый план выдвигается проблема агрегированного риска портфеля акций. Таким образом, при анализе финансовых активов важно учитывать не только колебания доходности конкретного актива, но и то, как включение этого актива в портфель отразится на изменчивости доходности портфеля. Риск, связанный с изменчивостью доходности отдельно взятого актива, называется общим риском. Общий риск распадается на две части (рис. 3.3). Доля общего риска, которую можно устранить путем формирования хорошо диверсифицированного портфеля, называется диверсифицируемым (несистематическим) риском. Этот риск может быть вызван событиями, специфическими для фирмы. Поскольку события, относящиеся только к отдельной фирме, носят случайный характер, их воздействие на инвестиционный портфель можно устранить с помощью диверсификации.
Рис. 3.3. Общий, диверсифицируемый и рыночный риск портфеля
Вторая часть общего риска – это рыночный риск, который представляет собой релевантный (эффективный) риск актива, если данный актив является частью хорошо диверсифицированного портфеля ценных бумаг, т.е. это воздействие данной акции на риск портфеля. Рассматриваемая в отдельности акция может быть высокорисковой, но если большую часть ее риска можно устранить с помощью диверсификации, то релевантный риск этой акции может оказаться низким. Чем больше воздействие акции на общий риск портфеля, тем выше рыночный риск акции. При этом увеличение количества акций одного вида в портфеле увеличивает риск портфеля. Рыночный риск является недиверсифицируемым (систематическим), т.е. его избежать невозможно. Он обусловлен возможностью глобальных событий, которые затрагивают всех участников рынка и последствия которых не могут быть устранены через диверсификацию. К таким событиям относятся война, инфляция, экономический спад, увеличение процентных ставок и т.п. Риск и доходность портфеля ценных бумаг можно измерить также при помощи ожидаемой доходности и вариации (СКО) доходности. Ожидаемая доходность портфеля представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных ценных бумаг, входящих в данный портфель:
где xi – доля портфеля, инвестируемая в i -й актив; Мерой риска портфеля может служить показатель среднего квадратического отклонения распределения доходности, совпадающий с формулой расчета СКО доходности отдельного актива. В этом случае необходимо знание доходности портфеля при разных состояниях экономики:
где rpi – доходность портфеля, соответствующая i -му состоянию экономики; Риск портфеля можно рассчитать и через показатели риска входящих в него активов. Однако эта связь не может быть выражена формулой средней арифметической – она носит более сложный характер. Для анализа этой связи используются ковариация и коэффициент корреляции. Ковариация – это мера, учитывающая дисперсию (разброс) индивидуальных значений доходности акции и силу связи между изменением доходности данной акции и всех других акций:
Cov (A, B) =
где Cov (A, B) – ковариация доходностей активов А и В; rАi (rВi) – доходность актива А (В), соответствующая i -му состоянию экономики; Ковариация также учитывает степень колеблемости доходности каждого из активов. Если доходность какого-либо из активов имеет большое СКО, то при наличии зависимости между активами значение Cov(А, В) будет большим. Однако при случайном характере колебаний Cov(А, В) будет все равно низкой. Аналогично, Cov(А, В) невелика, если мала колеблемость доходности одного из активов. При этом, если СКО доходности одного из активов равно нулю, то и Cov(А, В) равна нулю. Коэффициент корреляции позволяет стандартизировать ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и, значит, привести величины к сопоставимому виду. Он показывает силу и направление прямой связи между двумя переменными. Коэффициент корреляции доходности активов А и В (r А,В) рассчитывается по формуле
Следовательно, Cov(A, B) = r A,B s A s B. Стандартизация приводит к тому, что коэффициент корреляции лежит в пределах от –1,0 до +1,0. Знак коэффициента корреляции совпадает со знаком ковариации, поэтому при однонаправленном изменении переменных он положителен, при противоположном – отрицателен, а при слабой связи между переменными – близок к нулю. Если предположить, что распределения доходности отдельных ценных бумаг нормальны, то для определения риска портфеля из двух активов может использоваться следующая формула:
где s р, s А, s В – СКО портфеля, актива А и актива В соответственно; х – доля портфеля, инвестируемого в ценную бумагу А, и, следовательно, (1- х) – доля портфеля, инвестируемого в В. По мере увеличения числа акций в портфеле его риск будет уменьшаться, но не станет равным нулю. Сформировать портфель с нулевым риском можно было бы, если бы имелось достаточное число акций с нулевым или отрицательным коэффициентом корреляции. Однако обычно коэффициенты корреляции между отдельными акциями положительны, поэтому можно только снизить риск портфеля, но не устранить его полностью. Таким образом, изменяя состав и структуру портфеля финансовых активов, можно изменять его ожидаемую доходность и риск. Все портфели, которые при этом можно сформировать, образуют множество допустимых портфелей. Инвестора при этом интересуют только эффективные портфели. Эффективными называются портфели, обеспечивающие максимальную ожидаемую доходность при данном уровне риска или минимальный уровень риска для данной ожидаемой доходности. П р и м е р. Ожидаемая доходность актива А ( Допустимое множество в данном случае включает как портфели, состоящие только из актива А или только из актива В, так и портфели со всеми промежуточными комбинациями этих активов. Ограничимся рассмотрением пяти вариантов портфеля:
Как видим, портфель, состоящий только из актива А, неэффективен. Портфели, содержащие 25 и 50% актива В, генерируют большую ожидаемую доходность при меньшем риске, чем портфель из одного только актива А. Оставшиеся четыре портфеля являются эффективными, поскольку для каждого из них нельзя найти альтернативный портфель, характеризующийся меньшим риском при такой же доходности или большей доходностью при таком же риске. На рис. 3.4 множество допустимых портфелей обозначено как АВCDEG. Графическое изображение допустимого множества портфелей, состоящих из двух активов, представляет собой линию. При увеличении числа активов линия трансформируется в некоторую область (на рис. 3.4 пунктир означает условную границу; реально допустимое множество простирается за него). Граница ВCD определяет эффективное множество портфелей и называется границей эффективности. Портфели, лежащие слева и выше от нее, недоступны. Портфели справа от границы эффективности (внутренние портфели и портфели на линии АВ) неэффективны, поскольку при сохранении соответствующего уровня риска можно найти портфель с более высокой ожидаемой доходностью.
Рис. 3.4. Допустимое и эффективное множество портфелей
Портфель, оптимальный с точки зрения конкретного инвестора, зависит от его отношения к риску, проявляющегося в выборе параметров функции, описывающей взаимосвязь между риском и доходностью. Эта функция называется кривой безразличия. Она объединяет множество точек, которые представляют собой равнозначные (с одним уровнем полезности) с точки зрения инвестора комбинации риска и доходности. Множество кривых безразличия, представленных на графике (кривые I1, I2, I3; рис. 3.5), образует карту безразличия. Чем выше расположена кривая, тем более высокому уровню полезности для инвестора она соответствует.
Рис. 3.5. Оптимальный портфель инвестора
Оптимальный портфель с позиции отдельного инвестора – это точка касания границы эффективности допустимого множества портфелей и одной из кривых безразличия инвестора (Е на рис. 3.5). Эта точка соответствует наиболее высокому уровню удовлетворенности, которого может достичь инвестор при составлении портфеля из данных финансовых активов.
|


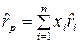 ,
, - ожидаемая доходность i -го актива; n – число активов в портфеле.
- ожидаемая доходность i -го актива; n – число активов в портфеле.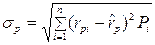 ,
, - ожидаемая доходность портфеля; Pi – вероятность того, что экономика будет находиться в i -м состоянии.
- ожидаемая доходность портфеля; Pi – вероятность того, что экономика будет находиться в i -м состоянии.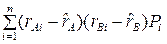 ,
,
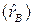 - ожидаемая доходность актива А (В); Pi – вероятность того, что экономика будет находиться в i -м состоянии. Если значения доходностей А и В изменяются в одинаковом направлении, то при любом состоянии экономики разности в скобках будут иметь одинаковый знак (либо обе положительные, либо обе отрицательные) и их произведение будет всегда положительным. Следовательно, Cov(А, В) также будет положительной. При изменении доходностей А и В в противоположных направлениях значение Cov(А, В) будет отрицательным. Если колебания доходностей двух активов носят случайных характер, произведение разностей в скобках будет то положительным, то отрицательным, а сумма произведений и, следовательно, значение Cov(А, В) будут стремиться к нулю. Это позволяет использовать ковариацию для оценки силы связи между доходностями активов.
- ожидаемая доходность актива А (В); Pi – вероятность того, что экономика будет находиться в i -м состоянии. Если значения доходностей А и В изменяются в одинаковом направлении, то при любом состоянии экономики разности в скобках будут иметь одинаковый знак (либо обе положительные, либо обе отрицательные) и их произведение будет всегда положительным. Следовательно, Cov(А, В) также будет положительной. При изменении доходностей А и В в противоположных направлениях значение Cov(А, В) будет отрицательным. Если колебания доходностей двух активов носят случайных характер, произведение разностей в скобках будет то положительным, то отрицательным, а сумма произведений и, следовательно, значение Cov(А, В) будут стремиться к нулю. Это позволяет использовать ковариацию для оценки силы связи между доходностями активов. .
. ,
,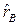 = 12% и s В = 10%. Коэффициент корреляции доходностей активов А и Вравен -1,0. Нам нужно определить множество допустимых портфелей и выделить из допустимого множества эффективное подмножество.
= 12% и s В = 10%. Коэффициент корреляции доходностей активов А и Вравен -1,0. Нам нужно определить множество допустимых портфелей и выделить из допустимого множества эффективное подмножество.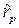 , %
, %





