Модель оценки доходности финансовых активов (CAPM)
Обращающиеся на рынке ценные бумаги имеют разный риск. Например, в Соединенных Штатах векселя Казначейства США считаются безрисковыми, так как доход по ним фиксирован и не подвержен влиянию рыночных событий. Их b -коэффициент равен 0. Рыночный портфель обыкновенных акций имеет b -коэффициент, равный 1,0, т.е. его риск выше безрисковых ценных бумаг. Однако инвесторы никогда не возьмут на себя риск без соответствующей компенсации. Поэтому они требуют от рыночного портфеля большей доходности, чем от безрисковых активов. Разница между доходностью рыночного портфеля и процентной ставкой по безрисковым бумагам представляет собой премию за рыночный риск. Соответственно за риск по финансовым активам, превышающий риск рыночного портфеля, инвесторы требуют и более высокой, чем рыночная, премии. Зависимость доходности финансовых активов от их риска рассматривается в модели оценки доходности финансовых активов (Capital Asset Pricing Model, или CAРМ). САРМ утверждает, что на конкурентном рынке ожидаемая премия за риск изменяется прямо пропорционально b -коэффициенту, т.е.:
Рассмотрим CAРM подробнее. В ее основу положены следующие допущения: 1. Основной целью каждого инвестора является максимизация возможного прироста своего достояния на конец планируемого периода. Решения принимаются на основе оценки ожидаемых значений доходности и средних квадратических отклонений альтернативных инвестиционных портфелей; 2. Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке rRF; ограничений на «короткие продажи» любых активов не существует; 3. Все инвесторы одинаково оценивают величину ожидаемых значений дисперсии и ковариации доходности всех активов, т.е. инвесторы обладают симметричной информацией; 4. Все активы абсолютно делимы и совершенно ликвидны, т.е. всегда могут быть проданы на рынке по существующей цене; 5. Не существует трансакционных затрат; 6. Не принимаются во внимание налоги; 7. Все инвесторы принимают цену как экзогенно заданную величину, т.е. все инвесторы предполагают, что их деятельность по покупке и продаже ценных бумаг не оказывает влияния на уровень их цен; 8. Количество всех финансовых активов заранее определено и фиксировано. На рис. 3.6 изображено множество эффективных рисковых портфелей (АВ) и кривых безразличия (I1, I2, I3), отображающих выбор между риском и ожидаемой доходностью для отдельного инвестора. Точка N отражает выбор оптимального портфеля из данного множества АВ. Однако инвестор может сделать лучший выбор, чем портфель N, если к возможному множеству рисковых портфелей подключить безрисковый актив с нулевым s и гарантированной доходностью rRF. Тогда инвесторы могут составить новые портфели и достичь любой комбинации риска и доходности на прямой линии, соединяющей rRF с М (где М – это точка касания прямой линии и границы эффективного множества портфелей акций). Портфели на этой линии будут предпочтительнее любого рискового портфеля на границе эффективности, поскольку позволяют достичь более высокой кривой безразличия, и поэтому представляют собой наилучшие достижимые комбинации риска и доходности.
Рис. 3.6. График САРМ
Имея новое множество возможностей, инвестор перейдет из точки N в точку R, которая лежит на более высокой кривой безразличия. Возможность перехода в точку R, соответствующую более высокому уровню удовлетворения, как раз и обуславливается комбинированием безрисковой ценной бумаги и рискового портфеля М. При условии соблюдения предпосылок САРМ все инвесторы должны иметь портфели, лежащие на линии rRF MZ и являющиеся комбинацией безрисковой ценной бумаги и рискового портфеля М. Таким образом, добавление безрискового актива ведет к изменению эффективного множества: теперь оно лежит на линии rRF MZ. Точное расположение портфеля инвестора определяется точкой касания кривой безразличия инвестора с линией rRF MZ. Линия rRF MZ называется линией рынка капитала (CML). Она пересекает ось доходности в точке, равной доходности безрискового актива rRF. Уравнение линии рынка капитала выглядит следующим образом:
Это уравнение показывает, что ожидаемая доходность эффективного портфеля равна сумме безрисковой ставки и премии за риск, исчисляемой умножением Следующий шаг в модели САРМ – переход от риска и доходности эффективных портфелей к риску и доходности отдельных ценных бумаг. Уравнение, устанавливающее связь между риском акции, измеряемым b, и доходностью акции, называется уравнением линии рынка ценных бумаг (SML):
ri = rRF + (rm-rRF)b,
где ri – требуемая доходность i -й акции (в условиях равновесия на рынке требуемые значения доходности должны равняться ожидаемым); rm – требуемая доходность рыночного портфеля («средней» акции портфеля); rm-rRF – рыночная премия за риск или цена риска для средней акции; b (rm-rRF) – премия за риск владения i -й акцией. При этом все инвестиции должны располагаться вдоль линии рынка ценных бумаг. На рис. 3.7 показано, что для безрисковых активов b -коэффициент равен 0 и премия за риск равна 0, а для рыночного портфеля b -коэффициент равен 1 и премия за риск равна (rm-rRF). Ожидаемая премия за риск инвестиций с b -коэффициентом, например равным 0,5, составляет половину ожидаемой премии за рыночный риск.
Рис. 3.7. График SML
Таким образом, требуемая доходность зависит от рыночного риска, измеряемого b, от безрисковой ставки и премии за рыночный риск. С изменением этих переменных меняется и SML. Основными факторами, вызывающими такие изменения, выступают инфляция, отношение к риску и b -коэффициент. Влияние инфляции проявляется прежде всего через безрисковую доходность. Эта доходность представляет собой номинальную ставку, состоящую из двух элементов: 1) реальной, безынфляционной доходности r* и 2) инфляционной премии IP, равной ожидаемому темпу инфляции. Следовательно, rRF = r*+IP. Если ожидаемый темп инфляции растет, то увеличивается и rRF. При этом SML сдвигается параллельно. Отношение инвесторов к риску отражается в крутизне SML: чем круче наклон, тем больше они избегают риска. При нейтральном отношении инвесторов к риску рисковые активы имели бы такую же ожидаемую доходность, как и безрисковые. При изменении степени неприятия риска инвесторами изменяется угол наклона SML (требуемая доходность при данном уровне риска). Варьируя структурой своих активов, а также используя внешние источники финансирования, фирма может изменять рисковость своих ценных бумаг, т.е. значение b -коэффициента. Бета-коэффициент может меняться и в результате роста конкуренции в отрасли, истечения срока действия основных патентов и т.п. При этом меняется и требуемая доходность.
|


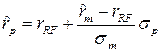 .
.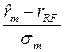 на среднее квадратическое отклонение портфеля. Следовательно, CML устанавливает линейную зависимость между ожидаемой доходностью и риском портфеля активов. При этом наклон CML, определяемый делением премии за рыночный риск на СКО рыночного портфеля, отражает совокупное отношение инвесторов к риску.
на среднее квадратическое отклонение портфеля. Следовательно, CML устанавливает линейную зависимость между ожидаемой доходностью и риском портфеля активов. При этом наклон CML, определяемый делением премии за рыночный риск на СКО рыночного портфеля, отражает совокупное отношение инвесторов к риску.



