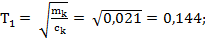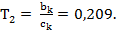ЛАБОРАТОРНАЯ РАБОТА № 2
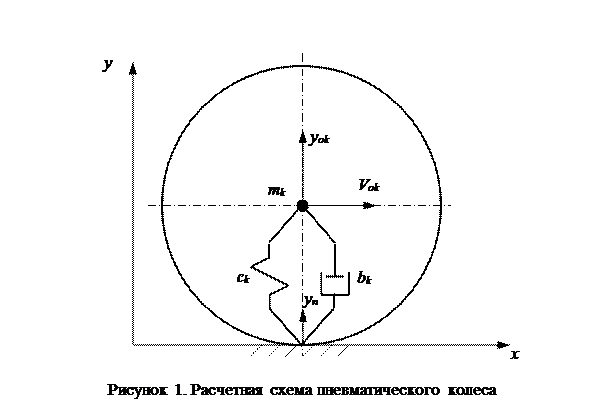
Цель работы: исследование динамических свойств упруго-вязкого пневматического колеса. Колесный пневматический движитель – одна из самых распространенных ходовых систем, как автомобильного транспорта, так и строительно-дорожной техники. Пневмоколесный движитель сглаживает кинематические возмущения, передаваемые от неровностей опорной поверхности к подвеске рамы машины, обеспечивая ей поступательное движение. Для исследования динамических свойств пневматического колеса необходимо составить его математическое описание, основанное на допущениях, расчетной схеме и аналитических зависимостях. Основные допущения при составлении расчетной схемы пневматического колеса: · поступательная скорость оси колеса Vоk постоянна; · упруго-вязкие свойства колеса представлены телом Фохта, представляющего собой соединение упругого и вязкого элемента; · силы сухого трения в пневматическом колесе отсутствуют. На основе принятых допущений составлена динамическая расчетная схема пневматического колеса (рисунок 1).
Основываясь на принципе Лагранжа-Даламбера можно утверждать, что при равномерном и прямолинейном движении оси колеса вертикальная сила, действующая на ось колеса, равна сумме сил образованных деформацией упругого и вязкого элементов тела Фохта. Сила, действующая на ось колеса равна:
где mк – масса приведенная к оси колеса, yок – координата оси колеса.
Сила, действующая от упругого элемента тела Фохта:
где ск – коэффициент жесткости упругого элемента, Δ y – деформация тела Фохта. Сила, действующая от вязкого элемента тела Фохта:
где bк – коэффициент вязкости вязкого элемента. Деформация тела Фохта определится разностью координат оси колеса yок и опорной поверхности yn:
Из уравнений (1 – 4) составим дифференциальное уравнение, отражающее динамику перемещения оси пневматического колеса:
Преобразовав (5), получим:
Заменив производную d/dt на оператор Лапласа р, получим передаточную функцию пневматического колеса:
где постоянные времени передаточной функции:
Для реализации передаточной функции пневматического колеса в среде MATLAB – Simulink воспользуемся блоком «Transfer Fcn» раздела Continuous, подставив в его числитель (Numerator) и знаменатель (Denomenator) соответствующие постоянные времени T (рисунок 2).
Рис. 1. Схема модели в MatLab Simulink
Расчетные данные: Полученные данные:
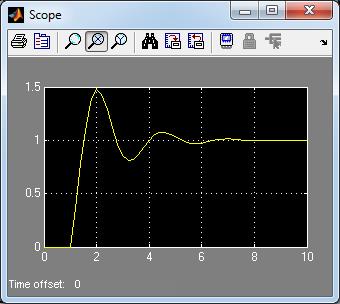
Рис. 2. Показания электронного осциллографа «Scope»
Рис. 3. Линеаризованная модель
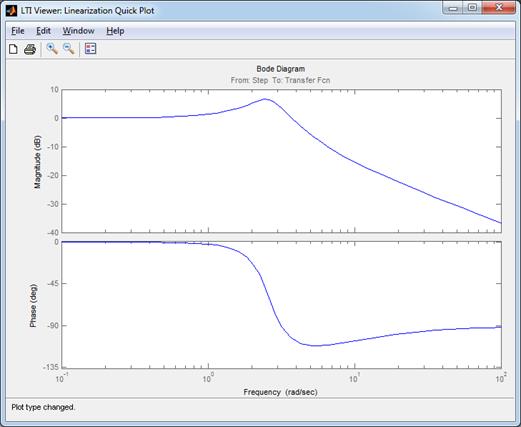
Рис. 4. ЛАХ и ЛФХ
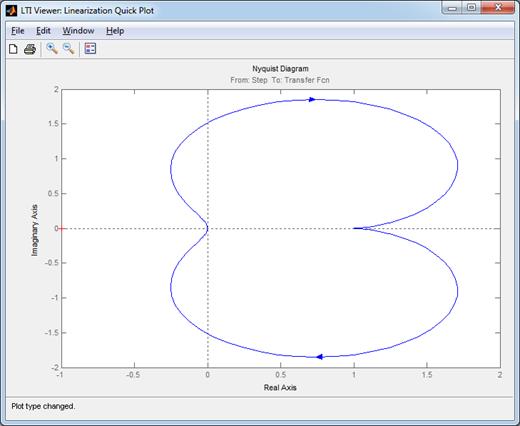
Рис. 5. АФЧХ
|

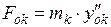 , (1)
, (1)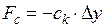 , (2)
, (2) , (3)
, (3)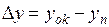 . (4)
. (4)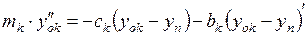 . (5)
. (5) . (6)
. (6)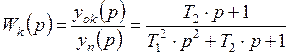 , (7)
, (7) и
и  . (8)
. (8)
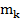 = 1210 кг;
= 1210 кг; 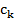 = 58000 H/м;
= 58000 H/м;  = 12100 H·c/м.
= 12100 H·c/м.