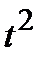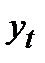Выравнивание по прямой линии
Аналитическое уравнение прямой линии имеет вид
где Для нахождения параметров уравнения
Аналитическое выравнивание можно существенно упростить соответствующим подбором значений t так, чтобы 1. Если число членов динамического ряда нечетное, то t следует отсчитывать от середины ряда. При таком отчете значение серединной даты (или периода) динамического ряда принимается равным нулю, ранние даты имеют отрицательные значения (–1; –2; –3 и т. д.), а поздние даты — положительные значения (1; 2; 3 и т. д.). 2. Если число членов ряда четное, то и в этом случае сохранятся требования о равных интервалах между всеми значениями t и о том, чтобы сумма всех значений t равнялась нулю. Подбор значений t производится так: находится серединная пара дат (или периодов) и значения t для нее принимают: –1 и +1, а далее вверх идут –3; –5; – и т. д., и вниз +3; +5; +7 и т. д. Расчет параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю ( если ряд содержит нечетное число членов
если ряд содержит четное число членов
где k – порядковый номер года; n – число лет в периоде. В табл. 8 приведены все необходимые данные для решения системы (9). Упрощенная система уравнений примет вид:
Отсюда
Подставив численные значения в выражение (11), получим
Подставим численные значения
Данное уравнение показывает, что число несчастных случаев снижается в среднем на 0,029 случая в год, т. е. параметр Подставляя в уравнение (12) соответствующие значения t из табл. 8, получим теоретические значения числа несчастных случаев Для оценки правильности выбора уравнения используется среднеквадратическое отклонение фактических уровней ряда от уровней, вычисленных по уравнению тренда
где n — число уровней ряда; р — число оцениваемых параметров в уравнении тренда (
Таблица 8. Вспомогательная таблица для определения параметров прямой линии
Таким образом, Коэффициент вариации рассчитываем по формуле (14) Как видим, изменения довольно значительные. Это можно объяснить тем, что мы рассматривали короткий ряд динамики.
|

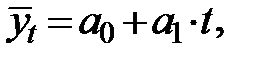 (8)
(8) — параметры, уравнения (8); t — показатель времени.
— параметры, уравнения (8); t — показатель времени. и
и 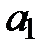 следует решить следующую систему уравнений
следует решить следующую систему уравнений , (9)
, (9)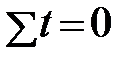 . При этом различают два случая:
. При этом различают два случая: ). При этом используют следующие формулы:
). При этом используют следующие формулы: ,
, ,
, , (10)
, (10) (11)
(11) и
и 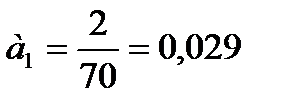
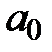 и
и  в уравнение прямой линии (8), получим НАПРИМЕР!!!!
в уравнение прямой линии (8), получим НАПРИМЕР!!!! (12)
(12) (координаты для построения прямой линии).
(координаты для построения прямой линии).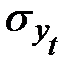 и коэффициент вариации V
и коэффициент вариации V
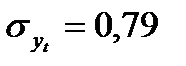 (13)
(13) и
и  ).
). (14)
(14)