линейное преобразование,- отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение  где Еи F - векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если
где Еи F - векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если 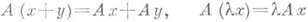 при всех
при всех 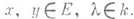 Простейшие примеры - нулевой Л. о. о, переводящий все векторы в
Простейшие примеры - нулевой Л. о. о, переводящий все векторы в  и (в случае E=F).тождественный Л. о. 1, оставляющий векторы на месте.
и (в случае E=F).тождественный Л. о. 1, оставляющий векторы на месте.
Понятие Л. о., будучи наряду с понятием векторного пространства главным в линейной алгебре, играет роль в самых разнообразных областях, математики и физики, прежде всего - в анализе и его приложениях.
Современное определение Л. о. впервые дал Дж, Пеано [1] (для  ). Оно было, однако, подготовлено предшествующим развитием математики, накопившей (начиная с линейной функции у=ах).огромное число примеров. В алгебре их неполный перечень включает линейные подстановки в системах линейных уравнений, умножение кватернионов и элементов грассмановой алгебры; в аналитич. еометрии - преобразования координат; в анализе - дифференциальные и интегральные преобразования и интеграл Фурье.
). Оно было, однако, подготовлено предшествующим развитием математики, накопившей (начиная с линейной функции у=ах).огромное число примеров. В алгебре их неполный перечень включает линейные подстановки в системах линейных уравнений, умножение кватернионов и элементов грассмановой алгебры; в аналитич. еометрии - преобразования координат; в анализе - дифференциальные и интегральные преобразования и интеграл Фурье.
Вплоть до начала 20 в. систематически изучались лишь Л. о. между конечномерными пространствами над полями  Первые "бесконечномерные" наблюдения, к тому же касающиеся общих полей, были сделаны О. Тёплицем [3]. Л. о. между бесконечномерными пространствами Е к F изучаются, как правило, в предположении их непрерывности относительно нек-рых топологий. Непрерывные Л. о., действующие в различных классах топологич. векторных пространств, в первую очередь банаховых и гильбертовых,- это основной объект изучения линейного функционального анализа.
Первые "бесконечномерные" наблюдения, к тому же касающиеся общих полей, были сделаны О. Тёплицем [3]. Л. о. между бесконечномерными пространствами Е к F изучаются, как правило, в предположении их непрерывности относительно нек-рых топологий. Непрерывные Л. о., действующие в различных классах топологич. векторных пространств, в первую очередь банаховых и гильбертовых,- это основной объект изучения линейного функционального анализа.
В теории Л. о. два специальных. случая F=k и F=E наиболее важны. В первом случае Л. о. наз. функционалом (см. Линейный функционал), во втором - линейным оператором, действующим в Е, или эндоморфизмом.
Все Л. о. из Ев Fобразуют векторное пространство 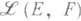 (вместо.
(вместо. 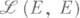 пишется
пишется  ) над kотносительно сложения и умножения на скаляр, задаваемыми формулами.
) над kотносительно сложения и умножения на скаляр, задаваемыми формулами.

 нулем является
нулем является  Умножение (композиция) АВ Л. о.
Умножение (композиция) АВ Л. о. 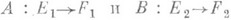 определено лишь при FZ=E! как последовательное применение Вн А. Относительно трех указанных операций
определено лишь при FZ=E! как последовательное применение Вн А. Относительно трех указанных операций 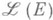 - пример ассоциативной алгебры над kс единицей 1. Это "больше чем пример": всякая ассоциативная алгебра над kвкладывается в
- пример ассоциативной алгебры над kс единицей 1. Это "больше чем пример": всякая ассоциативная алгебра над kвкладывается в 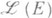 для нек-рого Е.
для нек-рого Е.
Векторные пространства над фиксированным полем (объекты) и Л. о. (морфизмы) образуют, вместе с законом композиции, категорию  Следующие понятия суть специальные случаи (применительно к
Следующие понятия суть специальные случаи (применительно к 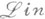 ) общекатегорных. Для Л. о.
) общекатегорных. Для Л. о. 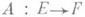 его ядром наз. подпространство
его ядром наз. подпространство  образом - подпространство
образом - подпространство  для нек-рого
для нек-рого  }, коядром - факторпространство Coker A= F/lm А. Л. о. Л наз. мономорфизм о м, если Кеr А= (0), и э п и м о р ф и з м о м, если 1m A = F. Л. о.
}, коядром - факторпространство Coker A= F/lm А. Л. о. Л наз. мономорфизм о м, если Кеr А= (0), и э п и м о р ф и з м о м, если 1m A = F. Л. о.  наз. левым (соответственно правым) обратным к A, если В А тождественен в Е(соответственно АВ - в F). Л. о. А -1, одновременно левый и правый обратный к А, наз. обратным к А. Л. о. (соответственно эндоморфизм), обладающий обратным, наз. изоморфизмом (соответственно автоморфизмом).
наз. левым (соответственно правым) обратным к A, если В А тождественен в Е(соответственно АВ - в F). Л. о. А -1, одновременно левый и правый обратный к А, наз. обратным к А. Л. о. (соответственно эндоморфизм), обладающий обратным, наз. изоморфизмом (соответственно автоморфизмом).

 где Еи F - векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если
где Еи F - векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если 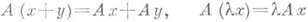 при всех
при всех 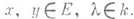 Простейшие примеры - нулевой Л. о. о, переводящий все векторы в
Простейшие примеры - нулевой Л. о. о, переводящий все векторы в  и (в случае E=F).тождественный Л. о. 1, оставляющий векторы на месте.
и (в случае E=F).тождественный Л. о. 1, оставляющий векторы на месте. ). Оно было, однако, подготовлено предшествующим развитием математики, накопившей (начиная с линейной функции у=ах).огромное число примеров. В алгебре их неполный перечень включает линейные подстановки в системах линейных уравнений, умножение кватернионов и элементов грассмановой алгебры; в аналитич. еометрии - преобразования координат; в анализе - дифференциальные и интегральные преобразования и интеграл Фурье.
). Оно было, однако, подготовлено предшествующим развитием математики, накопившей (начиная с линейной функции у=ах).огромное число примеров. В алгебре их неполный перечень включает линейные подстановки в системах линейных уравнений, умножение кватернионов и элементов грассмановой алгебры; в аналитич. еометрии - преобразования координат; в анализе - дифференциальные и интегральные преобразования и интеграл Фурье. Первые "бесконечномерные" наблюдения, к тому же касающиеся общих полей, были сделаны О. Тёплицем [3]. Л. о. между бесконечномерными пространствами Е к F изучаются, как правило, в предположении их непрерывности относительно нек-рых топологий. Непрерывные Л. о., действующие в различных классах топологич. векторных пространств, в первую очередь банаховых и гильбертовых,- это основной объект изучения линейного функционального анализа.
Первые "бесконечномерные" наблюдения, к тому же касающиеся общих полей, были сделаны О. Тёплицем [3]. Л. о. между бесконечномерными пространствами Е к F изучаются, как правило, в предположении их непрерывности относительно нек-рых топологий. Непрерывные Л. о., действующие в различных классах топологич. векторных пространств, в первую очередь банаховых и гильбертовых,- это основной объект изучения линейного функционального анализа.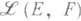 (вместо.
(вместо. 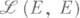 пишется
пишется  ) над kотносительно сложения и умножения на скаляр, задаваемыми формулами.
) над kотносительно сложения и умножения на скаляр, задаваемыми формулами.
 нулем является
нулем является  Умножение (композиция) АВ Л. о.
Умножение (композиция) АВ Л. о. 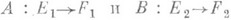 определено лишь при FZ=E! как последовательное применение Вн А. Относительно трех указанных операций
определено лишь при FZ=E! как последовательное применение Вн А. Относительно трех указанных операций 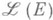 - пример ассоциативной алгебры над kс единицей 1. Это "больше чем пример": всякая ассоциативная алгебра над kвкладывается в
- пример ассоциативной алгебры над kс единицей 1. Это "больше чем пример": всякая ассоциативная алгебра над kвкладывается в 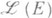 для нек-рого Е.
для нек-рого Е. Следующие понятия суть специальные случаи (применительно к
Следующие понятия суть специальные случаи (применительно к  ) общекатегорных. Для Л. о.
) общекатегорных. Для Л. о. 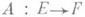 его ядром наз. подпространство
его ядром наз. подпространство  образом - подпространство
образом - подпространство  для нек-рого
для нек-рого  }, коядром - факторпространство Coker A= F/lm А. Л. о. Л наз. мономорфизм о м, если Кеr А= (0), и э п и м о р ф и з м о м, если 1m A = F. Л. о.
}, коядром - факторпространство Coker A= F/lm А. Л. о. Л наз. мономорфизм о м, если Кеr А= (0), и э п и м о р ф и з м о м, если 1m A = F. Л. о.  наз. левым (соответственно правым) обратным к A, если В А тождественен в Е(соответственно АВ - в F). Л. о. А -1, одновременно левый и правый обратный к А, наз. обратным к А. Л. о. (соответственно эндоморфизм), обладающий обратным, наз. изоморфизмом (соответственно автоморфизмом).
наз. левым (соответственно правым) обратным к A, если В А тождественен в Е(соответственно АВ - в F). Л. о. А -1, одновременно левый и правый обратный к А, наз. обратным к А. Л. о. (соответственно эндоморфизм), обладающий обратным, наз. изоморфизмом (соответственно автоморфизмом).


