Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n и пусть e1, e2,..., en - базис в X. Обозначим через A e1 = (a11,...,an1),..., A en = (a1n,...,ann) образы базисных векторов e1, e2,..., en.
Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно 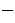 каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения

с одной стороны, связывают координаты образа y = A x с координатами прообраза X, с другой стороны, описывают действие оператора, заданного матрицей A.
При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве X произошел переход от базиса e = {e1,..., en} к базису e' = {e'1,..., e'n}. Связь между матрицей Ae оператора A в базисе e и матрицей Ae' этого оператора в базисе e' задается формулой
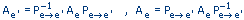
Здесь 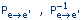 - матрица перехода от базиса e к базису e' и обратная к ней.
- матрица перехода от базиса e к базису e' и обратная к ней.
| |
Собственные значения и собственные векторы линейного оператора
Пусть A - линейный оператор, действующий в линейном пространстве.
Число называется собственным значением, а ненулевой вектор X - соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением A x = x.
Пусть A матрица оператора в некотором базисе.
Собственные значения оператора и соответствующие им собственные векторы связаны соотношением (A - E) x = 0, где E - единичная матрица, а 0 - нулевой элемент пространства X. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы (A - E) x = 0, которое существует тогда и только тогда, когда det (A - E) = 0. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения det (A - E) = 0, а собственные векторы -- как решения соответствующих однородных систем.
Уравнение det (A - E) = 0 называется характеристическим уравнением оператора, а многочлен det (A - E) характеристическим многочленом оператора.
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно ;
линейный оператор, действующий в n-мерном линейном пространстве имеет не более n различных собственных значений;
собственные векторы, отвечающие различным собственным значениям, линейно независимы;
если линейный оператор, действующий в n-мерном линейном пространстве X, имеет n различных собственных значений, то собственные векторы оператора образуют базис в пространстве X; этот базис называют собственным базисом оператора;
матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.
.
Приведение квадратичной формы
к каноническому виду
Рассмотрим квадратичную форму
 .
Выпишем ее матрицу и вектор-столбец переменных. .
Выпишем ее матрицу и вектор-столбец переменных.
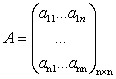 ; ;  .
Тогда квадратичную форму можно представить в виде .
Тогда квадратичную форму можно представить в виде
 - матричная запись квадратичной формы.
Пример. - матричная запись квадратичной формы.
Пример.  R. R.
 . .
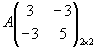 , , 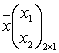 . .
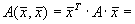  =
=  .
Определение 1. Если в некотором базисе квадратичная форма не содержит смешанных произведений переменных, т.е. .
Определение 1. Если в некотором базисе квадратичная форма не содержит смешанных произведений переменных, т.е.
 ,
то этот базис называют каноническим базисом данной квадратичной формы, а вид ,
то этот базис называют каноническим базисом данной квадратичной формы, а вид 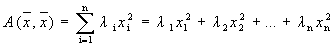 называют каноническим видом данной квадратичной формы.
Определение 2. Нормированием вектора называется нахождение вектора того же направления единичной длины. называют каноническим видом данной квадратичной формы.
Определение 2. Нормированием вектора называется нахождение вектора того же направления единичной длины.
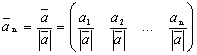 .
Теорема 1. Любую симметричную матрицу можно представить в виде A=U T DU, где D - диагональная матрица, у которой на диагонали расположены собственные числа матрицы А; U - матрица, составленная из нормированных собственных векторов матрицы А. Каждый вектор является столбцом.
Следовательно, любую квадратичную форму можно привести к каноническому виду с помощью некоторого ортогонального преобразования координат. Для всякой квадратичной формы существует канонический базис. .
Теорема 1. Любую симметричную матрицу можно представить в виде A=U T DU, где D - диагональная матрица, у которой на диагонали расположены собственные числа матрицы А; U - матрица, составленная из нормированных собственных векторов матрицы А. Каждый вектор является столбцом.
Следовательно, любую квадратичную форму можно привести к каноническому виду с помощью некоторого ортогонального преобразования координат. Для всякой квадратичной формы существует канонический базис.
 .
Если ввести новые переменные по формуле .
Если ввести новые переменные по формуле  , то квадратичная форма примет следующий вид: , то квадратичная форма примет следующий вид:
 - канонический вид квадратичной формы.
Из данного равенства видно, что коэффициентами в каноническом виде являются собственные числа матрицы А.
Теорема 2 (закон инерции квадратичных форм).В любом каноническом виде квадратичной формы количество положительных и отрицательных коэффициентов постоянно. - канонический вид квадратичной формы.
Из данного равенства видно, что коэффициентами в каноническом виде являются собственные числа матрицы А.
Теорема 2 (закон инерции квадратичных форм).В любом каноническом виде квадратичной формы количество положительных и отрицательных коэффициентов постоянно.
 Пример 1. Y X 1 Пример 1. Y X 1
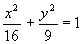 .
Если повернуть систему Y 1 X
координат на 900, то
уравнение примет вид .
Если повернуть систему Y 1 X
координат на 900, то
уравнение примет вид
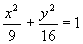 .
В этих базисах оба слагаемых со знаком "+".
Пример 2. Приведем квадратичную форму .
В этих базисах оба слагаемых со знаком "+".
Пример 2. Приведем квадратичную форму
 к каноническому виду. Выпишем ее матрицу. к каноническому виду. Выпишем ее матрицу.
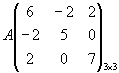 .
Найдем собственные значения матрицы квадратичной формы. Решим характеристическое уравнение. .
Найдем собственные значения матрицы квадратичной формы. Решим характеристическое уравнение.
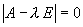 , ,
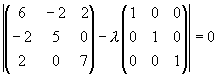 , ,
 , ,
 Корни данного уравнения являются делителями свободного члена. Разложим его на простые множители и подберем один из корней.
Корни данного уравнения являются делителями свободного члена. Разложим его на простые множители и подберем один из корней.
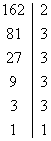
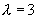 - является корнем. Разделим многочлен на линейный множитель l-3. - является корнем. Разделим многочлен на линейный множитель l-3.
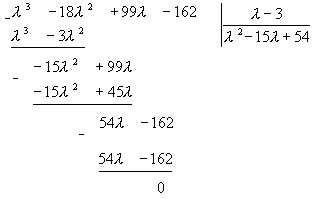 Найдем корни остатка.
Найдем корни остатка.
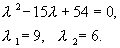 Получили три собственных значения матрицы. Найдем соответствующие им собственные векторы. Собственный вектор, соответствующий собственному значению l =3, найдем из уравнения
Получили три собственных значения матрицы. Найдем соответствующие им собственные векторы. Собственный вектор, соответствующий собственному значению l =3, найдем из уравнения  . .
 , ,
 , ,
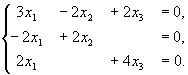
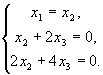 Пусть х 3= -1,
Пусть х 3= -1,
 или или  Итак, собственному значению
Итак, собственному значению  соответствует собственный вектор соответствует собственный вектор  .
Пронормируем собственный вектор. .
Пронормируем собственный вектор.   .
Аналогично находятся векторы .
Аналогично находятся векторы  . Базис, составленный из векторов . Базис, составленный из векторов  , является каноническим для данной квадратичной формы. , является каноническим для данной квадратичной формы.
 , ,
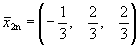 , ,
 .
В этом базисе квадратичная форма имеет вид .
В этом базисе квадратичная форма имеет вид  .
Формула преобразования координат имеет вид .
Формула преобразования координат имеет вид  , где , где
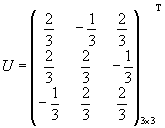 . .
|
| |
| |


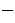 каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
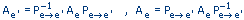
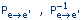 - матрица перехода от базиса e к базису e' и обратная к ней.
- матрица перехода от базиса e к базису e' и обратная к ней. .
Выпишем ее матрицу и вектор-столбец переменных.
.
Выпишем ее матрицу и вектор-столбец переменных.
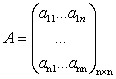 ;
;  .
Тогда квадратичную форму можно представить в виде
.
Тогда квадратичную форму можно представить в виде
 - матричная запись квадратичной формы.
Пример.
- матричная запись квадратичной формы.
Пример.  R.
R.
 .
.
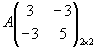 ,
, 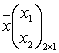 .
.
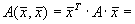
 =
=  .
Определение 1. Если в некотором базисе квадратичная форма не содержит смешанных произведений переменных, т.е.
.
Определение 1. Если в некотором базисе квадратичная форма не содержит смешанных произведений переменных, т.е.
 ,
то этот базис называют каноническим базисом данной квадратичной формы, а вид
,
то этот базис называют каноническим базисом данной квадратичной формы, а вид 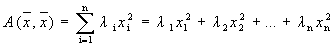 называют каноническим видом данной квадратичной формы.
Определение 2. Нормированием вектора называется нахождение вектора того же направления единичной длины.
называют каноническим видом данной квадратичной формы.
Определение 2. Нормированием вектора называется нахождение вектора того же направления единичной длины.
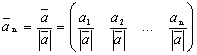 .
Теорема 1. Любую симметричную матрицу можно представить в виде A=U T DU, где D - диагональная матрица, у которой на диагонали расположены собственные числа матрицы А; U - матрица, составленная из нормированных собственных векторов матрицы А. Каждый вектор является столбцом.
Следовательно, любую квадратичную форму можно привести к каноническому виду с помощью некоторого ортогонального преобразования координат. Для всякой квадратичной формы существует канонический базис.
.
Теорема 1. Любую симметричную матрицу можно представить в виде A=U T DU, где D - диагональная матрица, у которой на диагонали расположены собственные числа матрицы А; U - матрица, составленная из нормированных собственных векторов матрицы А. Каждый вектор является столбцом.
Следовательно, любую квадратичную форму можно привести к каноническому виду с помощью некоторого ортогонального преобразования координат. Для всякой квадратичной формы существует канонический базис.
 .
Если ввести новые переменные по формуле
.
Если ввести новые переменные по формуле  , то квадратичная форма примет следующий вид:
, то квадратичная форма примет следующий вид:
 - канонический вид квадратичной формы.
Из данного равенства видно, что коэффициентами в каноническом виде являются собственные числа матрицы А.
Теорема 2 (закон инерции квадратичных форм).В любом каноническом виде квадратичной формы количество положительных и отрицательных коэффициентов постоянно.
- канонический вид квадратичной формы.
Из данного равенства видно, что коэффициентами в каноническом виде являются собственные числа матрицы А.
Теорема 2 (закон инерции квадратичных форм).В любом каноническом виде квадратичной формы количество положительных и отрицательных коэффициентов постоянно.
 Пример 1. Y X 1
Пример 1. Y X 1
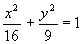 .
Если повернуть систему Y 1 X
координат на 900, то
уравнение примет вид
.
Если повернуть систему Y 1 X
координат на 900, то
уравнение примет вид
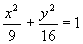 .
В этих базисах оба слагаемых со знаком "+".
Пример 2. Приведем квадратичную форму
.
В этих базисах оба слагаемых со знаком "+".
Пример 2. Приведем квадратичную форму
 к каноническому виду. Выпишем ее матрицу.
к каноническому виду. Выпишем ее матрицу.
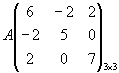 .
Найдем собственные значения матрицы квадратичной формы. Решим характеристическое уравнение.
.
Найдем собственные значения матрицы квадратичной формы. Решим характеристическое уравнение.
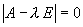 ,
,
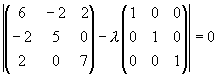 ,
,
 ,
,
 Корни данного уравнения являются делителями свободного члена. Разложим его на простые множители и подберем один из корней.
Корни данного уравнения являются делителями свободного члена. Разложим его на простые множители и подберем один из корней.
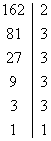
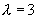 - является корнем. Разделим многочлен на линейный множитель l-3.
- является корнем. Разделим многочлен на линейный множитель l-3.
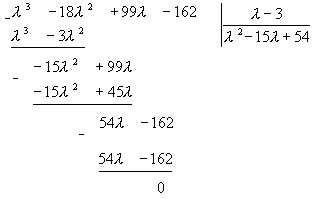 Найдем корни остатка.
Найдем корни остатка.
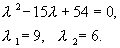 Получили три собственных значения матрицы. Найдем соответствующие им собственные векторы. Собственный вектор, соответствующий собственному значению l =3, найдем из уравнения
Получили три собственных значения матрицы. Найдем соответствующие им собственные векторы. Собственный вектор, соответствующий собственному значению l =3, найдем из уравнения  .
.
 ,
,
 ,
,
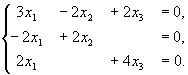
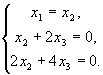 Пусть х 3= -1,
Пусть х 3= -1,
 или
или  Итак, собственному значению
Итак, собственному значению  соответствует собственный вектор
соответствует собственный вектор  .
Пронормируем собственный вектор.
.
Пронормируем собственный вектор. 
 .
Аналогично находятся векторы
.
Аналогично находятся векторы  . Базис, составленный из векторов
. Базис, составленный из векторов  , является каноническим для данной квадратичной формы.
, является каноническим для данной квадратичной формы.
 ,
,
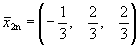 ,
,
 .
В этом базисе квадратичная форма имеет вид
.
В этом базисе квадратичная форма имеет вид  .
Формула преобразования координат имеет вид
.
Формула преобразования координат имеет вид 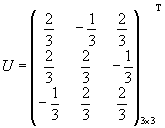 .
.



