Дисперсный анализ результатов регрессии
Так как в линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров, рассчитаем по каждому параметру стандартные ошибки:
Фактическое значение
Проверим справедливость равенства:
(расхождения за счет округления). При числе степеней свободы Так как
Так как
Для определения интервала прогноза по линейному уравнению регрессии рассчитаем: 1. Точечный прогноз
2. Средняя стандартная ошибка прогноза
Для прогнозируемого
Чтобы иметь общее суждение о качестве модели определим среднюю ошибку аппроксимации:
что говорит о хорошем качестве уравнения регрессии, так как ошибка в пределах 5 - 7 % свидетельствует о хорошем подборе модели к исходным данным.
|

 критерий
критерий
 и корреляции
и корреляции 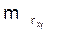
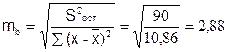 ;
; ;
;
 .
. критерия Стьюдента:
критерия Стьюдента: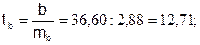
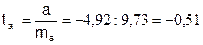 .
.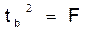

 и уровне значимости
и уровне значимости 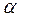 = 0,05 табличное значение
= 0,05 табличное значение 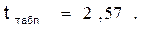
 (2,57<12,71), то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии
(2,57<12,71), то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии  определяется как
определяется как 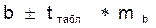 . 95 %-ные границы составят:
. 95 %-ные границы составят: ;
; .
.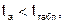 то
то  принимаем и считаем параметр
принимаем и считаем параметр 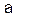 случайно отличным от нуля.
случайно отличным от нуля.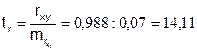
 (14,11>2,57), следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
(14,11>2,57), следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной. при прогнозном
при прогнозном  , составляющем 190 % от среднего уровня.
, составляющем 190 % от среднего уровня.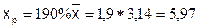 ;
;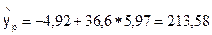 .
. .
.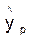 95 %-ный доверительный интервал при заданном
95 %-ный доверительный интервал при заданном 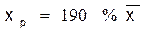 определяется выраженным:
определяется выраженным: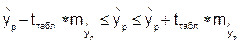 ;
; ;
; .
.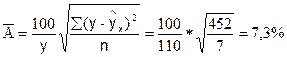 ,
,


