Система нормальных уравнений МНК будет иметь вид
Решая ее, получим:
Тогда, уравнение регрессии
Подставив в уравнение значения х, получим теоретические значения Коэффициент регрессии То, что В рассматриваемом примере имеем
Величина линейного коэффициента корреляции
что достаточно близко к 1 и означает наличие очень тесной зависимости затрат на производство от величины объема выпущенной продукции. Для оценки качества линейной функции рассчитаем коэффициент детерминации
Следовательно, уравнением регрессии объясняется 97,6 % дисперсии результативного признака, а на долю прочих факторов приходится лишь 2,4 % его дисперсии (то есть остаточная дисперсия). Так как Для оценки существенности линейной регрессии рассчитаем: 1. Общая сумма квадратов отклонений результативного признака
2. Факторная сумма квадратов
3. Остаточная сумма квадратов
4. Факторная дисперсия
5. Остаточная дисперсия
F – критерий Табличное значение Поскольку Таблица 2
|



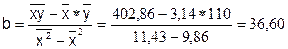
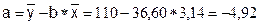
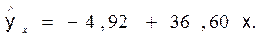
 (последний столбец табл. 1).
(последний столбец табл. 1). показывает, что при увеличении выпуска продукции на 1 тыс. единиц, затраты на производство по группе предприятий возрастут в среднем на 36,6 тыс. д. е.
показывает, что при увеличении выпуска продукции на 1 тыс. единиц, затраты на производство по группе предприятий возрастут в среднем на 36,6 тыс. д. е.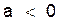 , соответствует опережению изменения результата над изменением фактора.
, соответствует опережению изменения результата над изменением фактора.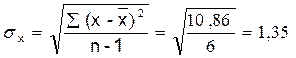


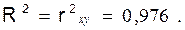
 близок к 1, следовательно, линейная модель хорошо аппроксимирует исходные данные и ее можно использовать для прогноза значений результативного признака.
близок к 1, следовательно, линейная модель хорошо аппроксимирует исходные данные и ее можно использовать для прогноза значений результативного признака. .
.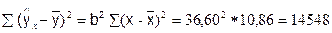 .
. .
. .
. .
.
 критерия для числа степеней свободы
критерия для числа степеней свободы 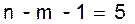 и уровня значимости
и уровня значимости  = 0,05 равно
= 0,05 равно 
 (161,64>6,61), то можно сделать вывод о значимости уравнения регрессии (связь доказана). Оценка значимости уравнения регрессии обычно делается в виде таблицы дисперсного анализа.
(161,64>6,61), то можно сделать вывод о значимости уравнения регрессии (связь доказана). Оценка значимости уравнения регрессии обычно делается в виде таблицы дисперсного анализа.


